* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download nonlinear optics in photonic structures - Dipartimento SBAI
Survey
Document related concepts
3D optical data storage wikipedia , lookup
Anti-reflective coating wikipedia , lookup
Ellipsometry wikipedia , lookup
Harold Hopkins (physicist) wikipedia , lookup
Retroreflector wikipedia , lookup
Silicon photonics wikipedia , lookup
Optical tweezers wikipedia , lookup
Optical rogue waves wikipedia , lookup
Gaseous detection device wikipedia , lookup
Surface plasmon resonance microscopy wikipedia , lookup
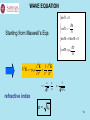
Photon scanning microscopy wikipedia , lookup
Magnetic circular dichroism wikipedia , lookup
Transcript
NONLINEAR NANOPTICS M. BERTOLOTTI Università di Roma “La Sapienza” Dipartimento SBAI Erice 2012 1 Index Introduction Linear and Nonlinear Systems Nonlinear Susceptibility Nonlinear Optical Interactions Nonlinearities in Metals Composite Materials Erice 2012 2 Introduction (1) It is now possible to fabricate artificial structures whose chemical compositions and shapes are controlled with a nanometer accuracy. These man-made systems are too small to behave like the bulk parent compounds and too big to behave like atoms or molecules. They may present new properties and because we can tailor some of these for specific purposes, nanostructures have the potential for revolutionary applications in electronics and optics. Furthermore, we know from the basic principle of quantum mechanics that when the size of a system becomes comparable to the characteristic length scale that determines the coherence of the wave functions, quantum size effects occur. The properties then become size and shape dependent. 3 Introduction (2) Optical properties in particular are very sensitive to quantum confinement. In semiconductors, for example, when a photon is absorbed it creates an electron-hole pair, and the two particles interact strongly by electrostatics. Because the effective masses are small and the dielectric constant large, the exciton (bound state of the electronhole pair) is large on the atomic scale. Depending on the material, the corresponding Bohr radius a0, which sets the natural length scale for all optical processes, is about 50 Å to 500 Å. One can observe massive changes in optical properties when the dimension of a semiconductor sample, in one or several directions, approaches a0. 4 Introduction (3) The optical response of a material is the average of the material properties in a volume larger than 3. In ordinary materials the ultimate blocks are atoms or molecules and the optical response is the refractive index n. Np P 0 E r 1 1 P 0 E n r 1 P 0 E p dipole moment of the atom, N number of atoms per unit volume. If the material is made by nanostructures with some optical properties, the optical response of the material is an average index nav which can be tailored according to the properties of the nanostructures. 5 Introduction (4) If the typical dimension of the structure is of the same order of , confinement effects may occur and the structure may behave as a resonant cavity. Some consequences are: - a change of the density of electromagnetic modes, - Electromagnetic field confinement and enhancement, - light velocity may be slowed down or become superluminal, - nonlinear processes may be modified, - suppression or enhancement of spontaneous emission may occur, - thermal radiation distribution may be modified. 6 Nonlinear Optics Linear and Nonlinear Systems A linear system is defined as one which has a response proportional to an external influence and has a well-known property, i.e. if influences, F1, F2 …., Fn are applied simultaneously, the response produced is the sum of the responses that would be produced if the influences were applied separately. A nonlinear system is one in which the response is not strictly proportional to the influence and the transfer of energy from one influence to another can occur. 7 If the influences are periodic in time, the response of a nonlinear system can contain frequencies different from those present in the influences. However, the point to emphasize here is that, as well as the generation of new frequencies, nonlinear optics provides the ability to control light with light and so to transfer information directly from one beam to another without the need to resort to electronics. Traditionally, nonlinear optics has been described phenomenologically in terms of the effect of an electric field on the polarization within a material. 8 MAXWELL EQUATIONS Electromagnetic processes are described by Maxwell’s equations which constitute a set of linear equations. In SI units: D D B B E E t t B 0B 0 D D H H J J t t div Ddiv D B B rot Erot E t t div Bdiv 0B 0 D D rot Hrot H J J t t where E and B are the electric and magnetic fields. The displacement fields D and H arise from the external charge and conduction current densities and J. In most cases of interest in nonlinear optics, = 0 and J = 0. 9 Constitutive relations connect the charge and current distributions within the medium and the displacement fields to the electric and magnetic fields. D P 0E E B H where P is the induced polarization in the medium resulting from the field E, is defined as a dielectric constant and 0 is the permittivity of free space (8.85 × 10-12 F m-1 in MKS units). Optical materials are mostly non magnetic = r 0 = 0. 10 LINEAR THEORY Usually one assumes a linear response of a dielectric material to an external field P 0E where P is the vector representing the electric dipole moment per unit volume induced by the external electric field E, 0 is vacuum permittivity and is a quantity characteristics of the considered material with no dimensions, called electric susceptibility. 11 In general is a tensor xx xy Px Py 0 yx yy Pz zx zy xz E x yz E y zz E z The symmetry properties of the material indicate which ones of the ij coefficients are zero. Alternatively Dx xx xy D y yx yy xz E x yz E y zx zz E z Dz zy 12 HOMOGENEOUS MATERIALS not depending on space div E div E rot E If B t rot E B t div B 0 div B 0 E B rot j t E rot B j t 0 0 j0 j0 div E div 0 E0 div B div 0 B0 B E B E rot E rot E rot B rot B t t t t 13 WAVE EQUATION div E 0 B rot E t Starting from Maxwell’s Eqs div B 0div B 0 D rot B 0 t 2E 1 2E E 0 2 2 2 t v t c c v r n 2 2E 1 2E E 0 2 2 2 t v t 2 v c c r n c 1 c 00 1 00 refractive index n r 14 DISPERSION Experimentally the refractive index is a function of wavelength (frequency) n( ) r ( ) r ( ) 1 ( ) This phenomenon is called DISPERSION. The polarization in a material medium can be explained considering the electrons tied to the atoms as harmonic oscillators. Nucleus: ~2000 electron mass, i.e., infinite mass 15 DISPERSION mx x kx eE0e Damping Restoring Force i t (one-dimensional model) Driving Force From the solution: eE0ei t x m(02 2 i ) m 02 k m E the induced moment is calculated: p ex e2 m 02 2 i e- x E0eit 16 For N oscillators per volume unit, the polarization is: N e2 it PNp E e 0 m 02 2 i Calling e2 m(02 i ) 2 atomic polarizability E E 0eit P N E 0 E N 0 where is the electric susceptibility. N 0 r 0 (1 ) 0 1 0 N 2 n 1 1 n r 0 17 2 Ne n2 1 2 2 0 m(0 i ) If the second term is lower than 1 (as it happens in gases): Ne2 n 1 2 0 m(02 2 i ) In the expression n comes out to be a complex number. 18 ABSORPTION The term i is responsible for absorption. The complex index can be written as Ne2 (02 2 ) Ne2 n n ik 1 i 2 2 2 2 2 2 2 2 2 0 m 0 2 0 m 0 2 2 If we consider a plane wave 1.0 E Aexp i(t kz) k c n 2 -1 ( a. u. ) where 0.5 0 n -0.5 -3.0 -1.5 0 1.5 3.0 0 19 we see that, substituting the complex refractive index, one has 2 k (n ik) which gives 2 k 2 n E A exp i t z exp z The last exponential represents a term of attenuation. The attenuation coefficient may be defined from: 1 dI 2 I(z) E I (0)e z I dz By comparison with the previous equation 2 k 2 n E A exp i t z exp z 4 k 20 It can be noticed that a small value of k leads to an elevated attenuation. k 0.0001 and 0.5m gives 25 cm 1. 1.0 ( a. u. ) k n -1 0.5 0 -0.5 -3.0 -1.5 0 1.5 3.0 0 Both n and k are functions of the frequency. 21 METALS In a metal the electrons are free and they do not oscillate around the atoms. Therefore k = 0 and 0 = 0. In the equation for n2 it is sufficient to put 0 = 0. 2 Ne n2 1 0m( 2 i ) N density of electrons If << n 1 2 p 2 2 p 2 For Al, Cu, Au, Ag Ne2 0 m Plasma frequency N ~ 1023 cm-3 and P~ 2.1016 s-1. 22 For > P n is real and the waves propagate freely. For P n is pure imaginary and the field is exponentially attenuated with the distance from the surface. Therefore the radiation is reflected from the surface. Therefore, for visible and infrared radiation < P and n is imaginary. In general, n is complex because of : i Ne2 Ne2 Ne2 2 1 n i 2 2 2 2 0m i i 0m 0m p i p 2 2 2 2 23 NONLINEAR SUSCEPTIBILITY Dipole moment per unit volume or polarization in the linear case Pi Pi ij E j 0 The general form of polarization in a nonlinear medium is Pi Pi χ E j χ 0 (1) ij (2) ijk E j Ek χ E j Ek El (3) ijkl 24 JUSTIFICATION OF THE PRESENCE OF A NONLINEAR RESPONSE If the force exercised by the electric field of the wave becomes comparable with the Coulomb’s force between the electron and the nucleus, the oscillator is perturbed (anharmonic oscillator) and, at the lower level of the perturbation, we can write: x(t) x(t) 02 x(t) Dx 2 (t) (e / m)E(t) E (4) x 25 The solution of eq.(4) can be expressed as the sum of two terms (1) (2) x(t) x (t) x (t) (5) in which x(1)(t) is obtained solving eq.(4) without the anharmonic term, whereas x(2)(t) is considered a small correction of the solution at the first order x(1)(t) and is obtained utilizing x(1)(t) in the anharmonic term x (2) (t) x (2) (t) 02 x (2) (t) 2 eE(t) (1) D x (t) . m (6) In this way, considering the case in which the forcing electric field is formed by the sum of two fields at different frequencies 1 E(t) E1 cos 1t E 2 cos 2 t E1e j1t E 2e j2 t c.c. 2 (7) 26 We have the solution at the first order 1 x (1) (t) x (1) ( 1 )e j1t x (1) ( 2 )e j2 t c.c. 2 (8) and subsequently the solution at the second order, solving eq.(6) with the use of (8) is 1 x (2) (t) [x (2) 1 2 e j 1 2 t x (2) 1 2 e j 1 2 t 2 x (2) 21 e j2 1t x (2) 22 e j2 2 t c.c] (9) in which x (2) x (2) 1 D(e / m) 2 E1E 2 1 2 2 02 12 j1 02 22 j2 02 1 2 2 j 1 2 1 D(e / m) 2 E 2k (2k ) ; k 1,2. 2 2 2 2 2 2 j 0 4k jk 0 k k (10) 27 Therefore the solution of the second order brings to the generation of oscillations at a frequency different from the ones of the forcing field. In particular, it is possible to have frequencies equal to the sum or to the difference of the field frequencies or to the double (second harmonic). Moreover, we emphasize that the previous formulas remain valid also if just a single forcing field is present. In this case x(2)(t) will be the sum of a second harmonic term (2) and a null pulsation term (term of optical rectification). 28 Remembering the expression for the medium polarization, we can write P(t) Ne x (1) (t) x (2) (t) (11) where N is the number of dipoles for volume unit P(t) PL (t) PNL (t) (12) which, compared with (10) x (2) x (2) 1 D(e / m) 2 E1E 2 1 2 2 02 12 j1 02 22 j2 02 1 2 2 j 1 2 1 D(e / m) 2 E 2k (2k ) ; k 1,2. 2 2 2 2 j 02 42k jk 0 k k permits to write (10) PL 0(1) E PNL (2) E E. (13) 29 SECOND HARMONIC PRODUCTION The nonlinear properties in the optical region have been demonstrated for the first time in 1961 by Franken et al. during an experiment of second harmonic generation. Sending red light of a ruby laser ( = 6.943 Å) onto a crystal of quartz, they observed ultraviolet light. 30 The story is that when Franken published his paper on the second harmonic production, the proof reader corrected the photo, suppressing the tiny spot of the second harmonic believing it was just a smash. You may see this on the photo below in which under the arrow you see….nothing! 31 In many crystals the nonlinear polarization depends on the direction of propagation, on the polarization of the electric field and on the orientation of the optical axis of the crystal. Since in such materials the vectors P and E are not necessarily parallel, the coefficient is a tensor. The second order polarization can be written as Pi(2) d ijk E jE k (14) j,k where i, j, k represent the coordinates x, y, z. The main part of the coefficients dijk, however, are usually zero and so only a few of them must be considered. 32 Only the non-centrosymmetric crystals can have a non null tensor dijk. In facts, let us consider an isotropic crystal. In this case dijk is independent from the direction and therefore it is constant. If now we invert the direction of the electric field, also the polarization must change sign, that is Pi(2) d ijk ( E j )( E k ) d ijk E jE k Pi(2) . It is clear that, not being able to be Pi(2) Pi(2) , dijk must be null. Moreover, in materials for which d ≠ 0, since no physical meaning can be assigned to an exchange of Ej with Ek, it must be dijk = dikj. 33 Now if we consider the Maxwell equations writing we have D 0 E P (15) D E P rot B j j 0 t t t B rot E . t (16) The polarization can be written as the sum of a linear term plus a nonlinear one P 0L E PNL (17) In case of materials with second order nonlinearity PNL may be written as PNL i dijk E jE k . (18) 34 So eq.(16) can be written, assuming j = 0 PNL E rot B t t (19) from which 2 2 PNL E 2 E 2 . 2 t t (20) If we consider the unidimensional case of propagation along a direction z, we have 2 (PNL )i Ei Ei 2 . 2 2 z t t 2 2 (21) 35 Let us consider now three monochromatic fields with frequencies 1, 2, 3 using the complex notation 1 E1i (z)e j 1t k1z c.c. 2 1 ( 2 ) E k (z, t) E 2k (z)e j 2 t k 2 z c.c. 2 1 j 3 t k 3z ( 3 ) E j (z, t) E 3 j (z)e c.c. 2 E (i 1 ) (z, t) (22) where the indices i, j, k represent the components x or y. The polarization at frequency 1 = 3 - 2, for example, from (18) and from (22) results Pi( 1 ) 1 j 3 2 t k 3 k 2 z d ijk E3 j (z)E 2k (z)e c.c. 2 j,k (23) 36 Substituting eqs.(22) into (21) for the component E1i, it is necessary to calculate 2 E( 1 ) 1 2 E (z)e 1t k1z c.c.. 2 2 1i 2 z z If we assume dE1i k1 dz d 2 E1i dz 2 (24) (25) we have 2 E(i 1 ) 1 2 dE1i (z) j 1t k1z k1 E1i (z) 2 jk1 e c.c. 2 2 dz z (26) with similar expressions for 2 E(j2 ) z 2 and 2 E(k3 ) . 2 z 37 Finally, substituting (26) and (23) into (21) we have dE1i (z) j 1 0 d ijk E3 jE2ke j k3 k2 k1 z c.c. dz 2 1 (27) and in analogous way dE2k j2 0 j k1 k 3 k 2 z d E E c.c. ijk 1i 3 je dz 2 2 3 0 j k1 k 2 k 3 z j d E E e c.c.. ijk 1i 2k dz 2 3 dE3 j (28) The second harmonic field is obtained immediately from (27) and (28) for the case of 1 = 2 and 3 = 21. Therefore it is enough to consider only, f.e., (27) 38 and the last one of (28). To further simplify the analysis we can assume that the power lost by the frequency 1 (fundamental) is negligible, and therefore dE1i dz 0. (29) So it is sufficient to consider just the last one of (28) dE2k j2 0 j k1 k 3 k 2 z d E E c.c. ijk 1i 3 je dz 2 2 dE3 j dz j 3 0 j k1 k 2 k 3 z d E E e c.c.. ijk 1i 2k 2 3 0 d jik E1i E1k e jkz dz 3 1 2 dE3 j where and j k k (3j) k1(i) k1(k) . (31) (28) (30) 39 In eq.(31) k1(i) is the constant of propagation of the beam at 1 polarized in the direction i. The solution of (30) for E3j(0) = 0 for a crystal of length L is or 0 e jkL 1 E3 j (L) j d jik E1i E1k jk 0 2 I(L) E3 j (L) 2 d jik E1i E1k 2 2 sen k L / 2 2 L . 2 k L / 2 (32) According to (32) a requirement for an efficient second harmonic generation is that k = 0, that is from (31) with 3 = 2, 1 = 2 = k k (3j) k1(i) k1(k) . k 2 2k( ) . (31) (33) 40 If k ≠ 0, the second harmonic wave generated at a generic plane z1 which propagates until another plane z2 is not in phase with that generated in z2. This produces an interference described by the factor sen 2 k L / 2 k L / 2 2 I(L) E3 j (L) 0 2 2 d jik E1i E1k 2 2 sen k L / 2 2 L . 2 k L / 2 (32) in (32). k 2 2k( ) . (33) The condition is never practically satisfied because, due to dispersion, the refractive index depends on . 41 In general we have k k (2 ) 2k ( ) 2 (2) ( ) n n c (34) being k ( ) ( ) n c (35) and therefore k 0. 42 Coherence length We have no more second harmonic production when sin(ΔkL/2)/ΔkL/2 = 0 This is achieved when ΔkL/2 =π Which means L = 2π/Δk L is named coherence lenght. However, it is possible to make k = 0 (phasematching condition) using various skills; the most used of which takes advantage from the natural birefringence of the anisotropic crystals. From (34) we can see that k = 0 implies n (2 ) n ( ) (36) k k (2 ) 2k ( ) 2 (2) n n( ) c (34) so that the refractive indices of second harmonic and of fundamental frequency have to be equal. Using birefringent materials it is possible to fulfill the condition of phase matching. 44 As another example a PBG may be used to obtain phase matching 45 Finally we point out that very well known electro-optic effects discovered in the XIX century are particular cases of nonlinear optics. Δεr = qEo Pockels effect P = εoχE εr = 1 + χ P = εoχE + χ(2) Eo E = εo(χ + χ(2) /εo Eo )E = εo χ’E χ’ = χ+ χ(2) /εo Eo 1+ εr + Δεr = 1 + εr +χ(2) /εo Eo Δεr = χ(2) / εo Eo 46 Kerr effect Δεr = qEo2 P = εoχE εr = 1 + χ P = εoχE + χ(3) Eo2 E = εo(χ + χ(3) /εo Eo2 )E = εo χ’E χ’ = χ+ χ(3) /εo Eo2 1+ εr + Δεr = 1 + εr +χ(3) /εo Eo2 Δεr = χ(3) / εo Eo2 47 Nonlinear Optical Interactions • The E-field of a laser beam ~ it E (t ) Ee C.C. • 2nd order nonlinear polarization ~ ( 2) P (t ) 2 ( 2) EE * ( ( 2) E 2 e 2it C.C.) 2 ( 2) 48 2nd Order Nonlinearities • The incident optical field ~ i1t i 2 t E (t ) E1e E2 e C.C. • Nonlinear polarization contains the following terms P(21 ) (2) E12 (SHG) P(22 ) (2) E22 (SHG) P(1 2 ) 2 (2) E1 E2 (SFG) summ frequency generation P(1 2 ) 2 (2) E1 E2* (DFG) difference frequency generation P(0) 2 (2) ( E1 E1* E2 E2* ) (OR) optical rectification 49 Sum Frequency Generation 2 2 ( 2) 1 Application: Tunable radiation in the UV Spectral region. 1 3 1 2 2 1 3 50 Difference Frequency Generation 2 1 2 ( 2) 1 Application: The low frequency photon, 2 amplifies in the presence of high frequency beam . This 1 is known as parametric amplification. 3 1 2 1 2 3 51 Phase Matching ( 2) 2 •Since the optical (NLO) media are dispersive, The fundamental and the harmonic signals have different propagation speeds inside the media. •The harmonic signals generated at different points interfere destructively with each other. 52 Third Order Nonlinearities When the general form of the incident electric field is in the following form, ~ i3t i1t i 2t E (t ) E1e E2e E3e The third order polarization will have 22 components i ,3i , (i j k ), (i j k ) (2i j ), (2i j ), i, j, k 1,2,3 The Intensity Dependent Refractive Index • The incident optical field ~ it E (t ) E ( )e C.C. • Third order nonlinear polarization P ( ) 3 ( ) | E ( ) | E ( ) ( 3) ( 3) 2 54 The total polarization can be written as P TOT ( ) E ( ) 3 ( ) | E ( ) | E ( ) (1) ( 3) 2 One can define an effective susceptibility eff (1) 4 | E ( ) |2 ( 3) The refractive index can be defined as usual n 1 4eff 2 55 By definition n n0 n2 I where n0 c 2 I | E ( ) | 2 12 2 ( 3) n2 2 n0 c 56 Typical values of nonlinear refractive index Mechanism n2 (cm2/W) ( 3) (esu) 1111 Response time (sec) Electronic Polarization 10-16 10-14 10-15 Molecular Orientation 10-14 10-12 10-12 Electrostriction 10-14 10-12 10-9 Saturated Atomic Absorption 10-10 10-8 10-8 Thermal effects 10-6 10-4 10-3 Photorefractive Effect large large Intensity dependent 57 Third order nonlinear susceptibility of some material Material 3 Response time Air 1.2×10-17 CO2 1.9×10-12 2 Ps GaAs (bulk room temperature) 6.5×10-4 20 ns CdSxSe1-x doped glass 10-8 30 ps GaAs/GaAlAs (MQW) 0.04 20 ns Optical glass (1-100)×10-14 Very fast 58 Nonlinearities in metals • In metals bulk production of second harmonic radiation is usually inhibited due to symmetry reasons and only an electric quadrupole and a magnetic dipole terms may be active • These reasons do not exhist at surface due to the lack of symmetry in a sheet region of the order of a few Å’s thickness between vacuum and the metal. In this case the discontinuity of the electric field is important • Therefore, although the production of radiation has a very low efficiency (~10-10) it is interesting to examine what happens 59 Nonlinearities in metals • A reasonable elementary model for a metal is an isotropic free electron gas. A consequence of this is that metals are opaque to visible radiation. • For frequencies lower than the plasma frequency, the electromagnetic radiation can penetrate only for a small depth (skin depth) of the order of the wavelength and due to their symmetry, bulk metals lack of dipole sources for second harmonic production. 60 Nonlinearities in metals • Within the skin depth of the incident electromagnetic field, there are, however, Lorentz forces on free (and to some degree also bound) electrons, as well as interband transitions, both of which lead to nonlinear bulk magnetic dipole polarization sources. 61 Nonlinearities in metals • Further, the breaking of inversion symmetry and the large change in dielectric constant at the metal-vacuum interface introduces strong surface currents within a few Fermi wavelengths of the surface which produce electric quadrupole terms. These mechanisms are however very weak. This notwithstanding, second harmonic generation from the surface of metals was studied since the beginning 62 Nonlinearities in metals Free electron gas theory The equation of motion for a free electron is d 2r e 1 E v B 2 m c dt (1) Damping is neglected for simplicity. Clearly, the only nonlinear term in this equation is the Lorentz force term. Since v << c in a plasma, the Lorentz force is much weaker than the Coulomb force, and then (e/mc)v B in (1) can be treated as a perturbation in the successive approximation of the solution. 63 Taking E Ε1e ik1 r i1t Ε2 e ik2 r i2 t + c.c. we have e ik1 r 0 i1t r (i )= Εe c.c. 2 i mi (1) r 2 1 2 ie2 m 12 1 2 2 2 Ε1 k2 Ε2 Ε2 k1 Ε1 e i k1 k2 r 0 i 1 2 t c.c. (2) and so on. 64 For a uniform plasma with an electronic charge density , the current density is given by JJ 1 2 J 1 2 r r t (3) with, for example, J 2 2 1 2 r 1 2 t 65 In a more rigorous treatment of an electron gas, we must also take into account the spatial variations of the electron density and velocity v. Two equations, the equation of motion and the continuity equation, are now necessary to describe the electron plasma: v p e 1 v v = E v B t m m c and v 0 t (4) where p is the pressure and m is the electron mass. The pressure gradient term in the equation of motion is responsible for the dispersion of plasma resonance, but in the following calculation we assume p = 0 for simplicity. 66 Then, coupled with (4), is the set of Maxwell’s equations 1 B E , c t 1 E 4J 4v B , c t c c (5) 0 E 4 , B 0 We assume here that there is a fixed positive charge background in the plasma to assure charge neutrality in the absence of external perturbation. Successive approximation can be used to find J as a function of E from (4) and (5). 67 We assume here that there is a fixed positive charge background in the plasma to assure charge neutrality in the absence of external perturbation. Successive approximation can be used to find J as a function of E from (4) and (5). Let (0) (1) v = v (1) v (2) (2) , , and j j(1) j(2) with (1) j (6) v (0) (1) and (2) j v (0) (2) v (1) (1) (7) 68 We shall find the expression for E Ε exp ik r it . j(2) (2) as an example assuming Substitution of (6) into (4) and (5) yields v (1) ( ) e iv (1) E, t m (1) () i(1) (0) v (1) t E 4(1) (), v (2) (2) e (1) i 2v (2) v (1) v (1) v B t mc (8) The second-order current density is then given by J (2) e2 ie2 2 2 E1 E1 2 E1 B1 m c m e E1 E1 i 4m i(0) (2) 2 (9) 69 Neglecting for the moment the (·E)E term, we may derive for the nonlinear polarization PNL E1 B1 E1 E1 (10) with ie3(0) 4m2 3c e 8m2 The term with is sometimes referred as the “magnetic dipole” and the one with as “electric quadrupole” source. The term E1 ()E1 strictly vanishes in reflection SHG, but it can be non-zero in more complicated geometries, including it. Both terms are always polarized in the incidence plane (TM mode). The first term is always present and is directed along k The second term arises only if the fundamental wave is polarized in the incidence plane. 70 Adler for the first time speaks, for the centrosymmetric media, of two source terms for SH, one due to the magnetic dipole, due to the Lorentz force, and one due to the electric quadrupole, through the Coulomb force. 71 Including the (·E)E term of (9), which can be transformed as: e2 ie2 E E E B 2 2 1 1 1 1 m2 c m e E1 E1 i 4m i(0) J (2) (2) 2 where e e E E 2 (0) v(1) E i 4m m ie2 2 3 (0) E E m ie2 (0) E 2 3 E m 1 2p / 2 (9) (11) 1/ 2 is the plasma resonance frequency. With (11), B c / i E, and the vector relation E E E E 12 E E , the current density in (9) can be written as p 4(0) e / m i(0) e2 ie2 E E 2 3 (0) E E 2 3 4m m i(0) e2 ie2 (0) E E E 2 3 E (12) 4m 2 3 m 1 2p / 2 J (2) 2 Eq.(9) shows explicitly that aside from the Lorentz term, there are also terms related to the spatial variation of E. They arise from the nonuniformity of the plasma. In a uniform plasma, (0) = 0 and · E = 0 from (11). This means that k is perpendicular to E and therefore (E · )E also vanishes. The Lorentz term is the only term in J(2)(2) 72 Coming back to (9), we may now write PNL E1 E1 E1 E1 instead of (10) where (13) . e3n0 2 4 8m In the bulk the electric field is divergenceless and only the first term in (13) contributes: near the surface both terms are important. 73 Jha used the model of the free electron gas in order to explain the SH in the metals and for first he wrote the second order polarization with the two terms, that represent the contribution of bulk and surface. 74 We look first at the component of PNL parallel to the surface, PNL ; since E1 is continuous across the surface, using translational symmetry in the plane of the surface we find PNL E1 1z / z , (14) which gives a Dirac delta function at the surface in the limit of a step function equilibrium density profile. Thus there is an effective current PNL sheet radiating at 2 at the surface, and following back the E1z , derivation of eq.(14) it is clear that results from the accumulated charge at the surface, signaled by the rapid variation in being PNL driven by the component of the electric field parallel to the surface. The magnitude of the current sheet due to may be calculated in the free electron theory, since eq.(13) may be integrated across the surface. 75 For the normal component of PNL the situation is different. From eq.(13) we find z 2 E z z z PNL E1 E1 1 , z z (15) which is ambiguous, since both and E1z change discontinuously across the surface. Obviously, PNLz , which appears in part because of the rapid variation of the normal field and in part because the response of electrons near the surface need not display inversion symmetry (1), is more subtle in nature than PNL . We note that even if the integral of eq.(15) could be performed, it is not clear whether the current sheet should be placed just inside or just outside the surface. This point is an ambiguity in the free electron model. (1) J.Rudnick and E.A.Stern, PR B4 (1971) 4274 (2) J.E.Sipe et al. Solid State Comm. 34 (1980) 523; PR B21 (1980) 4389 76 We conclude that the free electron theory only leads to physically meaningful results for the first order fields if a step function profile is adopted for the equilibrium electron density; in that limit, however, well-defined predictions for the second harmonic generation cannot be made. Of course, one would certainly expect the free electron theory to be less than accurate in the surface region where the actual fields vary over distances on the order of a few Fermi wavelengths; the point we wish to stress here is that the theory is in a sense somewhat worse: it is inherently ambiguous. If people use the free electron theory to describe SHG, a number of essentially arbitrary “prescriptions” are given for determining the magnitude and placement of the second harmonic current sheet; in z some instances, PNL is simply neglected. 77 In conclusion, the term E x B originating from the Lorentz force acts on the current produced at the first order by B (it is nonlinear in B). It is a bulk current in the metal and does not irradiate except if there is a boundary. The second term is a surface electric quadrupole term. It is present in nonlinear reflection from a metal and originates from the discontinuity of the normal component of E at the interface which generates nonlinear currents. The surface currents are a tangential component and a bulk one directed along z. The SH polarization from the perpendicular and parallel surface currents can be written as and Pzsurface (2) a()Ez ()Ez () surface Px (2) b()E x ()E z ( ) 78 Rudnick and Stern (1971) argued from physical grounds that the second harmonic current sheet should be placed outside the bulk metal, and that its magnitude should be specified in terms of parameters a and b of order unity. These conclusions are borne out to some extent by the application of the hydrodynamic theory of the electron gas to the calculation of SHG. The sheet is called selvedge (Sipe, Surf. Sci. 84, p. 75, 1979) and is smaller than . It is to be placed outside the bulk metal. The free electron theory does not place unambiguously the current sheet. J.Rudnick and E.A.Stern, PR B4 (1971) 4274 79 Dependence on fundamental beam polarization direction • A typical apparatus is shown in the figure Sample L2 Prism m 0n 80 HP-F /2 BS m 0n L1 40 • Since the surface nonlinear sources are in the simplest theory proportional to (·E)E, then incident fields polarized only in the plane of the surface (normal to the plane of incidence) do not contribute to the harmonic signal. A Dichroic filters VA Laser System PM • However the bulk terms proportional to E×H lead to harmonic generation for all incidence polarizations 80 Experimental Setup s (TE) f90 f p (TM) Sample f0 L2 Prism nm 0 80 High Pass band filter HP-F /2 Neutral density filters 800 nm 150 fs 1 kHz m 0n 40 L1 A BS Dichroic filters VA Laser System PM 81 Dependence on fundamental beam polarization direction • Neglecting bulk terms, a [ cosf ]4 dependence on the polarization is predicted, where f is the electric field angle relative to the plane of incidence. • Deviations from this relation are indicative of contributions from the bulk term, and in particular the ratio • M = ISH (f90) / ISH (f0) • yields information about the relative strengths of the surface versus bulk terms s (TE) • • • F.Brown et al., PRL 14 (1965) 1029 F.Brown and R.E.Parks, PRL 16 (1966) 507 N. Bloembergen et al., PR 174 (1968) 813 f90 f p (TM)f0 82 First experimental results 83 Composite materials • It is possible to combine two or more optical materials in such a manner that the effective nonlinear optical susceptibility of the composite material exceeds those of its constituents. • Some structure is shown in the figure. In each case, the characteristic distance scale over which the constituent materials are mixed is much smaller than an optical wavelength. • Consequently, the propagation of a beam of ligth through such material can be described by spatially averaged values of the linear and nonlinear refractive indices obtained by performing suitable volume averages. • J.E. Sipe and R.W.Boyd, PR A46 (1992) 1614; JOSA B11 (1994) 297 G.L.Fischer et al. PRL 74 (1995) 1871 • 84 Structures • If the two constituent materials of the composite posses different linear refractive indices, the electric field of the incident laser beam will become spatially nonuniform within the material. Under proper conditions, the electric field amplitude will become concentrated in the more nonlinear constituent of the composite, resulting in an enhanced overall nonlinear optical response. 85 • Much of the early work on composite nonlinear optical materials concerned metallic colloids. • For such materials, an enhancement of the electric field occurs in the vicinity of each metallic particle. • The enhancement is particularly large when the laser frequency is near that of the surface plasmon resonance of the metallic particle • • D.Ricard et al. Opt. Lett. 10 (1985) 511 F.Hache et al. Appl. Phys. A47 (1988) 347 86 Spherical particles a << dispersed with a very low volume fraction f << 1. A single spherical inclusion experiences a local field Eloc Eloc E and the field inside it is Ei 4 P 3 h 3 h Eloc i 2 n (28) (29) If the inclusion is made of a metal with Re( i ) 0 one may choose the host and the inclusion dielectric constant such that Re( i 2 h ) 0 corresponding to the plasmon resonances, thus obtaining resonant enhancement effects. Thus the inclusion can experience an enhanced local field that, in case of several inclusions randomly dispersed in the host, leads to an effective dielectric constant eff that satisfies eff h f with i h (30) eff 2 h i 2 h where f is the volume fraction of the inclusion material. 87 Similar effects can be obtained with dielectric particles. In this case the most spectacular effects are obtained when the size of the particle is smaller than the exciton orbits in semiconductor. Quantum effects appear 88 Nonlinear optical properties of CdSe quantum-dot doped glasses As an example Fig.1 shows typical room-temperature, linear low intensity, absorption spectra of CdSe QDs doped glasses. Distinct discrete absorption lines as well as blue shift of the lowest energy electrohole transition (absorption edge) with decreasing microcrystallite size are clearly seen. S.H.Park, M.P.Casey, J.Falk, JAP 73 (1993) 8041 89 The results of a measurement of the 567 nm transmission of the 26 A sample as a function of laser intensity is shown in the figure 90