Download The Euler Line and the Nine-Point

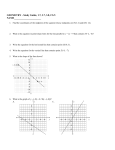
Mathematical Exploration:
The Euler Line and the
Nine-Point-Circle
Theorems
Student A
Introduction
The Euler Line Theorem was first founded by Leonhard Euler in 1765 and the NinePoint-Circle Theorem was first proven by Jean- Victor Poncelet and Charles Brianchon in 1821.
The two theorems explore the geometrical aspects of any triangle, except an equilateral triangle,
using dilations and three theorems that are more well-known than the two theorems being
explored. The three theorems are: the perpendicular bisects of the sides of a triangle intersect at
the center of the circumscribed circle called the circumcenter, the medians intersect at a point
that is two-thirds the distance from any vertex to the midpoint of the opposite side called the
centriod, and the lines containing the altitudes of the triangle intersect at the orthocenter. This
topic was chosen so that I could gain more mathematical insight on geometry that I had
overlooked and not learned in the past. Through this exploration I hope to pass on the knowledge
I obtained about the Euler Line Theorem and the Nine-Point-Circle Theorem, because the
theorems will help further understanding the role of geometric functions.
Definition of dilation: A dilation is a type of transformation, where the image is similar to the
preimage, because a dilation shrinks or stretches the preimage. A dilation has a center of dilation,
one point about which all the other points are transformed, and a scale factor, which shows how
much the image is shrunken or stretched. Dilations are written in this notation: DA,r (P)=P’, in
which A is the center of dilation, r is the scale factor, and P is the point being dilated. If r > 1,
then the image is a stretch of the preimage, and if r < 1 the image is a shrink of the preimage.
We first look at the Euler Line Theorem and in order to understand the theorem, we will
examine dilations and their effect on triangles. When given two points P and A and a real number
r, if P≠A the dilation DA,r (P)=P’ such that the distance of AP ' = r AP , DA,r (A)=A, and if r>0
then P’ lies on AP but if r<0 then P’ lies on a ray in the opposite direction of AP . To help
understand dilations better, we can visualize three dilations using the diagrams below.
In Figure 1, the dilation causes AB ' to be one-half of AB , so r =
1
. In Figure 2, AB ' is
2
twice as AB , so B ' is on a ray that exceeds AB and r = 2 . In Figure 3, the dilation causes B ' to
1
be on a ray in the opposite direction of AB and AB ' is one-half of AB , so r = − .
2
Using similar triangles, we can also visualize dilation. As shown by Figure 4 below, in a
triangle, ABC, the points B and C are dilated, DA,r. Since
C' A B' A
=
= r , ΔABC is similar
CA
BA
to ΔAB ' C ' , because both triangles share < A . From this we are able to conclude that the images
are parallel to the preimages and in any given dilation DA,r, if DA,r (B)=B’ and DA,r (C)=C’, then
B ' C ' = r BC .
We are able to apply the concept of dilations to prove that dilations map segments, rays,
and lines so that the images are also segments, rays, and lines as well as preserve angles
measures, parallelism, and perpendicularity. Using segments, as shown above by Figures 1, 2,
and 3, when we dilated the point B, a new segment AB ' is formed. Let us say that there is a point
X lying on a segment BC and DA,r (X)=X’, then X’ is on B ' C ' , because B ' X '+ X ' C ' = B ' C ' .
This can be proven by Figure 5 or using the theorem, in any given dilation DA,r, if DA,r (B)=B’
and DA,r (C)=C’, then B ' C ' = r BC :
B ' X '+ X ' C ' = r BX + r CB ⇒
B ' X '+ X ' C ' = r ( BX + XC ) ⇒
B ' X '+ X ' C ' = r BC ⇒
r BC = B ' C ' ⇒
B ' X '+ X ' C ' = B ' C '
As a result, we conclude that the dilation image of BC was B ' C ' , and since X’ lies
on B ' C ' , the dilation image of a segment is also a segment. Using the same method, we can
prove that the dilation image of a ray and a line are also a ray and a line.
As shown by Figure 6, there are two triangles, ΔPBC and ΔP ' B ' C ' . The two triangles
are similar triangles, because
P 'C ' P ' B ' C ' B '
=
=
= r . Because ΔPBC ~ ΔP ' B ' C ' , the
PC
PB
CB
corresponding angle measures within the two triangles are equal. Since dilations preserve angle
measures, they also preserve parallelism and perpendicularity, because parallelism and
perpendicularity depend on angles.
When polygons are dilated, the image is also a polygon. This can be proven using a
square and the dilation image of the square inside a triangle as shown by Figure 7. In Figure 7,
DA,r (P1)=P1’, DA,r (P2)=P2’, DA,r (P3)=P3’, and DA,r (P4)=P4‘ and since it is given that P1P2P3P4
is a square, the angles of P1’P2’P3’P4’ are all right angles, because of what we proved in the
previous page. Since all the angles are right angles, we conclude that the image is a square, so all
the sides of the image are congruent. Therefore, the image of a square is a similar square, so the
image of a polygon is a similar polygon.
Now that we understand dilations, we can combine the conclusions made from dilations
in order to understand the Euler Line Theorem. In Figure 8, ΔABC with centriod P has ΔEFG
as its image under the dilation DP,-1/2. The dilation causes B to be mapped onto F, A to be mapped
on to E, and C to be mapped on to G, because r = −
1
so the F, E, and G are on the ray opposite
2
of PA , PB , and PC respectively. Since the preimage is a triangle, the image is a similar
triangle, so ΔABC ~ ΔEFG . A centriod is two-thirds the distance from a vertex to the midpoint
of the opposite side, so G is the midpoint of AB and PG is one-half of CP , F is the midpoint of
AC and FP is one-half of PB , and E is the midpoint of BC and PE is one-half of AP . Also,
since the medians intersect at the centriod, CG intersects AE and BF at P.
Using Figure 9 we can prove the Euler Line Theorem which states that in any triangle,
the circumcenter , the centriod, and the orthocenter are collinear and the distance from the
centriod to the orthocenter is twice the distance from the centriod to the circumcenter.
As shown by Figure 9, ΔABC has a centriod of P, where the medians CG , BF , and
AE intersect and an orthocenter of O, where the altitudes BK and CH intersect.
ΔABC undergoes a dilation DP,-1/2 and as proven above in the previous pages, the image of a
triangle under a dilation transformation is a similar triangle, so ΔABC ~ ΔEFG . Since G is the
midpoint of AB , H ' G is perpendicular to FE , and FE is parallel to AB , H ' G is the
perpendicular bisector of AB . In the same way, FK ' is the perpendicular bisector of AC . Since
FK ' intersects H ' G at O ' , O ' is where the perpendicular bisectors intersect, the circumcenter.
Therefore, the DP,-1/2 maps the orthocenter onto the circumcenter. Because an image, the dilation
center, and the preimage are all collinear, the centriod P, the orthocenter O, and the circumcenter
O ' are all collinear and r =
1
, O ' P is one-half of OP . Therefore, ΔABC completely proves the
2
Euler Line Theorem.
Now using the Euler Line Theorem, we are able to prove the Nine-Point-Circle Theorem
which states that in any triangle, the midpoints of the sides, the feet of the altitudes, and the
midpoints of the segments joining the vertices to the orthocenter all lie on the circle with radius
one-half the radius of the circumscribed circle and centered at the midpoint of the segment
joining the orthocenter to the circumcenter. Using Figure 10 below, we can visualize and
understand the Nine-Point-Circle Theorem.
As proven before by the Euler Line Theorem, orthocenter O, centriod P, and
circumcenter Q are collinear. We are able to construct the nine- point circle using the Euler line
and several other defined points. Above on the circle lie E, F, and G, which are the midpoints of
the sides BC , AC , and AB respectively. There are points T, H, and I that are the feet of the
altitudes of the triangle. The segments that connect the orthocenter with the vertices, AO , CO ,
and BO , have midpoints J, K, and L respectively, which also lie on the circle. In order to prove
the Nine-Point-Circle Theorem, we have to prove that N, the midpoint of OQ , is the center of the
circle, on which the nine points stated above lie. Since N is the midpoint of OQ and QP is one1
OQ
NP 6
1
1 1 1
third of OQ , we know that NP is one-sixth of QP , because − = , and thus
=
= ,
1
NQ
2 3 6
OQ 2
3
so NP is one-half of NQ . When we perform the dilation, DP,-1/2, then DP,-1/2 (C) = G and DP,-1/2
1
1
(Q) = N. Thus, NG is the image of QC , so NG = QC , because r = . Since CG is the radius
2
2
of the circumscribed circle, so NG is one-half the radius of the circumscribed circle. Since K
and N are the midpoints of OC and OQ respectively, NK is one-half the radius of the
1
circumscribed circle, because NK = QC .
2
As shown by Figure 11, GH had a midpoint R, then NR is the perpendicular bisector
of GH , because N is the midpoint of OQ and, as shown in Figure 9, QG // OH // NR , because
they all are perpendicular to AB . Since NR is the perpendicular bisector of GH , we could
1
1
1
conclude that NG = NH . Above we found that NK = QC and NG = QC , so NH = QC .
2
2
2
This means that NH = NK = NG =
1
radius of the circumscribed circle. Using the same
2
methods, we find that NT = NL = NF =
NI = NJ = NE =
1
radius of the circumscribed circle and
2
1
radius of the circumscribed circle. As a result, E, F, G, J, K, L, H, I, and T
2
are all equal distant from N and lie on the same circle, so N is the center of the circle that has a
radius of one-half of the circumscribed circle and thus proves the Nine-Point-Circle Theorem.
Although dilations were used in order to explain the Euler Line and Nine-Point-Circle Theorems,
similar triangles and coordinate geometry may be used as well.
Using Figure 12, we can show how to find the Euler Line by coordinate geometry. In
Figure 12, three points, A, B, and C, create triangle ABC. Point D is the midpoint of AB ,
⎛ x + x y + y2 ⎞ ⎛ −6 + 6 10 + 4 ⎞
because ⎜ 1 2 , 1
,
⎟=⎜
⎟ = (0,7) . Now we must find the perpendicular
2 ⎠ ⎝ 2
2 ⎠
⎝ 2
bisector of AB and in order to do so, we must find the slope perpendicular to AB . The slope of
AB is
Δy 6 + 6 −1
−1
, so the slope of the perpendicular bisector is
=
=
⋅ slope = −1 ⇒ slope = 2 .
Δx 4 − 6 2
2
The equation of the perpendicular bisector of AB is
y − y1 = m( x − x1 ) ⇒
y − 7 = 2( x − 0) ⇒
y = 2x + 7
⎛ x + x + x3 y1 + y2 + y3 ⎞
The centroid can be found using the formula: centroid = ⎜ 1 2
,
⎟ . By
3
3
⎝
⎠
⎛ x + x + x y + y2 + y3 ⎞ ⎛ −6 + 6 − 6 −8 + 4 + 10 ⎞
simple substitution, centroid = ⎜ 1 2 3 , 1
,
⎟=⎜
⎟ , the point
3
3
3
3
⎝
⎠ ⎝
⎠
of the centroid is ( −2, 2) .
Using Figure 13 below, we can visualize the centroid on triangle ABC.
Let us now find the point of the circumcenter for triangle ABC using coordinate
geometry. First we must find the midpoint of BC . The midpoint of BC , point F, is (0, −2) ,
⎛ x + x y + y2 ⎞ ⎛ 6 + 6 4 − 8 ⎞
because ⎜ 1 2 , 1
,
⎟=⎜
⎟ = (6, −2) . Then we need to find the equation of the
2 ⎠ ⎝ 2
2 ⎠
⎝ 2
perpendicular bisector of BC , so we must find the slope of BC . The slope of BC is
Δy 4 + 8
=
= 1 , so the slope of the perpendicular is 1 ⋅ slope = −1 ⇒ slope = −1 . Therefore, the
Δx 6 + 6
equation of the perpendicular bisector of BC is
y − y1 = m( x − x1 ) ⇒
y + 2 = −1( x − 0) ⇒
y = −x − 2
The point of the circumcenter is the point of intersection between the perpendicular
bisector of BC and the perpendicular bisector of AB . The point of the circumcenter is ( −3,1) ,
because
−x − 2 = 2x + 7 ⇒
−9 = 3 x ⇒
x = −3 ⇒
y = 2( −3) + 7 = 1
This can be visualized using Figure 14 below.
The Euler Line can be found without the orthocenter, because by definition, the Euler
Line contains the circumcenter, orthocenter, and centroid. Therefore, a line that passes the
circumcenter and the centroid must also pass the orthocenter. The Euler line of triangle ABC
is y = x + 4 , because
Δy
2 −1
=
=1⇒
Δx −2 + 3
y −1 = x + 3 ⇒
y = x+4
The Euler Line of triangle ABC is represented graphically below by Figure 15.
As shown by dilations, once the Euler Line is found, the Nine-Point Circle can be found
as well. Therefore, coordinate geometry is one of the methods that can be used to prove the Euler
Line and Nine-Point Circle Theorems.
Conclusion
The theorems proved and the conclusions made in this exploration make us encounter
new knowledge on geometry. The Euler Line Theorem establishes that the circumcenter,
centriod, and orthocenter are collinear and that the distance between the centriod and the
orthocenter is twice the distance between the circumcenter and the centriod, while the NinePoint-Circle Theorem establishes that nine determined points all lie on one circle with a center
that is the midpoint of the segment which connects the orthocenter and the circumcenter. We
may have already been exposed to transformations in geometry, but when we explore the Euler
Line Theorem and the Nine-Point-Circle Theorem, we apply transformations in order to
understand geometry that appears to be not obvious. As well as function, coordinate geometry is
a method of discovering the Euler Line and the Nine-Point Circle Theorem. By using geometric
functions and coordinate geometry, this exploration offers brief and understandable proofs to the
theorems.
Bibliography
Bogomolny, Alexander. “The Euler Line and the 9-Point Circle.” Interactive Mathematics
Miscellany and Puzzles. N.p., 2012. Web. 29 Feb. 2012. <http://www.cut-theknot.org//.shtml>.
Eccles, Frank M. “The Euler Line and Nine-Point-Circle Theorems.” Mathematics Teacher
(1999): 50-54. Web. 1 Mar. 2012.
Joyce, David E. “The Euler Line of a Triangle.” Clark University. N.p., Mar. 1996. Web. 29 Feb.
2012. <http://aleph0.clarku.edu/~djoyce///.html>.
Roberts, Donna. “Dilations.” Regents Exam Prep Center. N.p., 2012. Web. 29 Feb. 2012.
<http://regentsprep.org/////.htm>.
Simmons, Bruce. “Centroid Formula.” Mathwords. N.p., 24 Mar. 2011. Web. 1 Apr. 2012.
<http://www.mathwords.com//_formula.htm>.