Download here

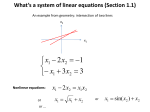
Introduction to linear systems
Consider two lines in the plane.
Example 1
x+y = 1
2 x + y = 1.
Solution: x = 0, y = 1.
Geometric interpretation: the two lines intersect at a single point.
Introduction to linear systems
Consider two lines in the plane.
Example 1
x+y = 1
2 x + y = 1.
Solution: x = 0, y = 1.
Geometric interpretation: the two lines intersect at a single point.
Example 2
2x+
y = 1
−4 x − 2 y = −2.
Solution: infinitely many solutions. Thinking of y as a f ree variable,
x
y
!
=
1
2
0
!
+y
1
−2
1
!
.
Geometric interpretation: the two lines are equivalent.
Example 2
2x+
y = 1
−4 x − 2 y = −2.
Solution: infinitely many solutions. Thinking of y as a f ree variable,
x
y
!
=
1
2
0
!
+y
1
−2
1
!
.
Geometric interpretation: the two lines are equivalent.
Example 3
2x + 3y = 1
2x + 3y = 2.
Solution: no solutions.
Geometric interpretation: the two lines are parallel.
Example 3
2x + 3y = 1
2x + 3y = 2.
Solution: no solutions.
Geometric interpretation: the two lines are parallel.
Two lines in R × R either:
• intersect in exactly one point (unique solution), or
• are equal (infinitely many solutions), or
• are parallel (no solutions).
Think about the geometry!!
(Q 51 from notes) A porcelain company manufactures ceramic cups
and saucers. For each cup or saucer, a worker measures a fixed
amount of material, and puts it in a forming machine where it is glazed
and dried. On average, this takes three minutes per cup and two
minutes per saucer. The materials for a cup cost 15cents, and a
saucer 10cents. In exactly eight hours of work, a worker uses $24
worth of materials. Can you determine how many cups and how many
saucers are made?
So, we can handle two linear equations with two unknowns.... what
about the more general case?
Definition A system of m linear equations in n unknowns is one of
the form:
a11 x1
a21 x1
+ a12 x2 + · · · + a1n xn = b1
+ a22 x2 + · · · + a2n xn = b2
..
..
..
am1 x1 + am2 x2 + · · · + amn xn = bm
where each aij and bi is a real number.
The variables (or unknowns) are x1, . . . , xn. The numbers aij are
constants and are called the coefficients of the system, and the numbers bi are sometimes called the right-hand side (or RHS).
Example A system of three equations with four unknowns:
2x −
y − z + 2w = 1
6x − 2y + z + 6w = 4
2x
− z + 3 w = 4.
Does it have any solutions? If any, how many, and what are they?
Definition A solution to an m × n system is an assignment of numbers to each of x1, . . . , xn so that all m equations are satisfied. A
system is consistent if it has at least one solution. Otherwise it is inconsistent. The general solution to a consistent system is the set
of all solutions.
Systems in Echelon form
Definition The leading variables (or pivots) of a system are those
variables that are the first in one of the equations. The other variables
are free variables.
Definition A system is in Echelon Form (EF) if each equation has a
pivot (ignoring equations of the form 0 = 0), and each pivot is further
to the right as we move down.
Echelon form: yes or no?
Example
x1 +2 x2 +x3 −x4
+ x6
x2
−x4 +x5
x4
+3 x6
x5 +2 x6
=
=
=
=
3
0
3
4.
Echelon form: yes or no?
Example
x+y = 1
x−y = 7
To solve a system in echelon form, we work up from the last equation
expressing the value of each leading variable in terms of the free
ones.
The general solution:
x1
x2
x4
x5
=
8 − x3 − 2 x6
= −1
−
x6
=
3
− 3 x6
=
4
− 2 x6
with x3, x6 ∈ R.
Any choice of real values for the free variables x3 and x6 determines
a solution to the system.
The same solution, using vector notation:










or:
x1
x2
x3
x4
x5
x6


8








 −1 





 0 

=
+x 
3 

 3 









 4 

0
−1
0
1
0
0
0





+x
6





−2



 −1 


 0 


 −3  ,




 −2 
1










x1
x2
x3
x4
x5
x6


8




 −1 




 0 


=

 3 +s






 4 

0










−1
0
1
0
0
0





+t





−2



 −1 


 0 


 −3  ,




 −2 
1
s, t ∈ R.
Algorithm for solving a system in Echelon Form
1. Identify the leading and free variables.
2. Assign a parameter to each free variable.
3. Work up from the last to the first equation, solving by substitution (back substitution).
4. [Optional] Write the solution in vector form.