Download Cross Products

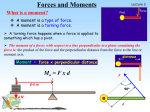
3.2 Cross Products
The cross product is only defined for vectors in three dimensions. For three
dimensional vectors u and v that are specified by a magnitude and direction, the cross
product uv is the vector defined as follows.
1.
uv points in the direction perpendicular to u and v. Its
direction is determined by the right hand rule. Position your
right hand so the fingers lie along u and curl toward v. Your
thumb should point in the direction of uv.
2.
magnitude of uv =
(magnitude of u) (magnitude of projection of v on the plane perpendicular to u)
= | u | | v | sin
= area of parallelogram with sides u and v
1
= 2 (area of triangle with sides u and v)
where
 = angle between u and v
Alternatively, to form uv from u and v do the following.
1. Project v on the plane perpendicular to u.
2. Rotate that vector counterclockwise by 90 in the plane perpendicular to u
when viewed from the u direction.
3. Multiply that vector by | u |.
Note that if u and v point in the same direction then uv is zero.
Torque. One application of the cross product is to
calculating the torque of a force acting on an object. Suppose
we have an object that occupies more than a single point in
space. Let C be the center of mass of the object (or some other
designated point on the object). Suppose a force F acts on the
object at some point on the object. Let
r = vector from the C to where the force is applied.
Then
 = the torque due to the force
= rF
1-1
The torque turns out to be a good description of the rotating effect of the force. In fact,
the force has two effects.
1.
The center of mass of the object moves as if all the mass of the object
were concentrated at the center of mass and the force acted at the center of
mass.
2.
The object tends to rotate about the axis through . The rotating power of
the force depends on
a. The distance | r | of the point of application of the force from the
center of mass.
b. The magnitude of the projection of the force on the plane
perpendicular to r.
In fact the rotating power of the force is equal to
| r | | F | sin = magnitude of  = |  |
Quantitatively one has
d
I dt = |  |
where
I = moment of inertia of object about the axis through 
 = angular velocity about the axis through r  F
In fact the above equation extends to a vector equation
d
I dt = 
where
I = moment of inertia matrix of the object
 = angular velocity vector
Example. (Problem #40 on p. 824 of the text) A certain object consists of two
rods each 4 ft long and joined at a right angle at the one of the ends of each rod. The first
rod extends from P 4 ft to the right to a point R. The second rod goes down 4 ft from R to
a point Q. A force F of 36 lb acts at Q and points in the plane of the rod down and to the
left at an angle of 30 with respect to the horizontal. Find the torque due to the force with
respect to the point P.

Solution. Let r = PQ be the directed line segment from P to Q. Then the torque
 = r  F. One has
|  | = | r | | F | sin
where  = angle between r and F = 45 + 60 = 105. So
|  | = (4 2 ft) (36 lb) sin105
= 144 2 sin105 ft-lb
= 144 (1.414) (0.9659) ft-lb
= 196.7 ft-lb
 is directed perpendicular to the plane of the rod.
1-2
Algebraic properties of the cross product. The cross product has the following
algebraic properties. In the following u, v and w are any vectors and t is any number.
1.
uv = - vu
(the cross product is antisymmetric)
2.
uu = 0
3.
(tu)v = t (uv)
(the cross product is homogeneous)
4.
(u + v)w = uv + vw
(distributive)
u  (v + w) = uv + uw
(distributive)
5.
ii = 0
ij = k
ik = - j
ji = - k
jj = 0
jk = i
ki = j
kj = - i
kk = 0
Sketch of proof. (1) This follows from the fact that when you use the right hand
rule to find the direction of vu, it points in the opposite direction as the direction of uv.
(2) This follows from the fact that the angle between u and itself is zero.
(3) Consider the case t > 0. Note that both tu and u have the same direction. Therefore
(tu)v and uv have the same direction. So (tu)v and t(uv) have the same direction.
Furthermore (tu)v and t (uv) have the same magnitude.
(4) This is a little more subtle. It follows from the fact that projecting on the plane
perpendicular to u, rotating about the line through u and multiplying by u all preserve
sums.
(5) The fact that ii = 0, jj = 0 and kk = 0 all follow from property (2). To see that
ij = k, note that k is perpendicular to i and j and has the correct direction determined by
the right hand rule. Also it has the correct length for ij. The other relations are proved
in the same fashion.
1-3