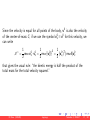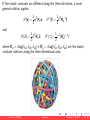Download 02PCYQW_2016_Lagrange_approach - LaDiSpe

Lagrange Approach
Basilio Bona
DAUIN – Politecnico di Torino
Semester 1, 2016-17
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
1 / 50
Introduction
A multibody system is considered as a system in which the dynamic
equations derive from a unifying principle.
This principle is based on the fact that, in order to describe the motion of
a system, it is sufficient to consider some scalar quantities.
These quantities were in origin called vis viva and work function, today
they are called kinetic energy and potential energy.
Both are state functions, i.e., functions that map the value of the state
vector into a scalar function.
The concept of state will be defined later; for the moment we simply
consider that the state corresponds to the two vectors of the generalized
coordinates q(t) and of the generalized velocities q̇(t).
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
2 / 50
This general principle is called the Principle of Least Action.
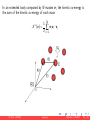
Let us consider the space Q of the generalized coordinates q ∈ Q, as
sketched in Figure for a two-dimensional space Q.
A particle starts its motion at time t1 in Q1 = q(t1 ) and ends it motion at
time t2 reaching the state Q2 = q(t2 ) (or vice-versa, since time can be
reversed).
Assume that the motion keeps constant the total energy, i.e., the sum
E = K + P of the kinetic energy K and the potential energy P that the
particle has at time t1 .
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
3 / 50
Q1 and Q2 are connected by a continuous path (trajectory) called true
trajectory , that is unknown, since it is what we want to compute as the
result of the dynamical equation analysis.
If we choose at random different trajectories, with the only condition that
the two boundary points remain the same (perturbed trajectories), the
chance to obtain exactly the true trajectory will be very small.
What characterizes the true trajectory with respect to all possible other
perturbed trajectories?
Euler contributed to the solution of this problem, but Lagrange developed
a complete theory, that was later extended by Hamilton.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
4 / 50
The true trajectory is the one that minimizes the integral of the vis-viva
(i.e., twice the kinetic energy) of the entire motion between Q1 and Q2 .
This integral is called action and has a constant and well defined value for
each perturbed trajectory having constant total energy E (E depends only
on the initial state).
The least action principle states that the nature “chooses”, among the
infinite number of trajectories starting in q(t1 ) and ending in q(t2 ), the
trajectory that minimizes the definite integral
Z t2
S=
t1
K ∗ (q(t), q̇(t))dt
of a particular state function K ∗ (q(t), q̇(t)).
The integral between the initial time t1 and the final time t2 must obey to
the boundary constraints in the two time instants.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
5 / 50
The scalar quantity S is the integral of a function and is called a
functional.
A functional is a mapping between a function and a real number; the
function shall be considered as a whole, i.e., not a single particular value;
in this sense a functional is often the integral of the function.
The minimization of a functional is based on a particular mathematical
technique, called calculus of variations.
The conditions that guarantee the minimization of S provide a set of
differential equations that contain the first and second time derivatives of
the qi (t); this set of equations completely describes the system
dynamics.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
6 / 50
These differential equations specify the evolution of a physical quantity
as the result of infinitesimal increments of time or position; summing up
this infinitesimal variations we obtain the physical variables at every
instant, knowing only their initial value and possibly some initial derivative:
we can say that the motion has a local representation.
The action characterizes the motion dynamics requiring only the
knowledge of the states at the initial and final times; every intermediate
value of the variables can be determined by the minimization of the action,
that is a global, rather than a local, measure.
The Lagrange approach is based on the definition of two scalar quantities,
namely
the total kinetic co-energy K
∗
and the total potential energy P
associated with the body.
The reason for using the term co-energy instead of the term energy , will
be clarified later.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
7 / 50
Lagrangian approach
The Lagrange method allows to define a set of Lagrange equations, that
have some advantages with respect to the vector equations provided by
the Newton-Euler approach.
The approach provides n second-order scalar differential equations,
directly expressed in the generalized coordinates q̇i (t) e qi (t).
If holonomic constraint are present, the constraint forces do not
appear in the equations.
The kinetic co-energies and the potential energies are independent of
the reference frame used to represent the body motion.
The kinetic co-energies and the potential energies are additive scalars:
in a multi-body system the total energies/co-energies are the sum of
each energy/co-energy component.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
8 / 50
Linear and angular momenta
Linear momentum hL is the physical vector defined as the product of a
body mass M for its linear velocity v (the center-of-mass velocity)
hL (t) = Mv(t)
In non-relativistic mechanics the mass M of a body is constant (except for
some particular cases, as rockets consuming fuel, etc.)
Angular momentum hA (also called moment of momentum or rotational
momentum) is the physical vector defined as the product of a body
rotational inertia Γ for its rotational velocity ω
hA (t) = Γ(t)ω(t)
While the mass of a body is usually constant, the inertia matrix (or inertia
tensor) Γ may vary in time.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
9 / 50
Kinetic energy and co-energy for single point-mass
The mechanical kinetic energy associated to a point-mass m is defined
as the work necessary to increase the linear or angular momentum from 0
to h, i.e.,
Z
K (h) =
h
dW
0
The infinitesimal work associated to the mass is given by
dW = f · dx + τ · dα
where the symbol · indicates the scalar product, and f is the resultant of
the applied linear forces on the mass, dx is the infinitesimal linear
displacement increment, τ is the resultant of the applied angular torques,
and dα is the infinitesimal angular displacement increment. Moreover
f=
B. Bona (DAUIN)
dhL
dt
τ=
Lagrange
dhA
dt
Semester 1, 2016-17
10 / 50
The resulting infinitesimal work is therefore the sum of two terms
dW = dWL + dWA =
dhA
dhL
· dx +
· dα = v · dhL + ω · dhA
dt
dt
and we can write
K (h) =
Z h
0
v · dhL + ω · dhA
The kinetic energy is a scalar state function associated to the particle
states (v, ω) and (hL , hA ).
Another state function associated to the point-mass, called mechanical
kinetic co-energy, is defined as
∗
K (v) =
Z v
0
hL · dv + hL · dω
As shown in Figure, between the mechanical energy and the co-energy a
relation exists
K ∗ (v) = h · v − K (h)
(for notational simplicity, only the linear velocity is considered)
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
11 / 50
Figure: This relation is an example of the Legendre transformation
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
12 / 50
In particular, if the mass particle is moving at a velocity significantly
smaller that the speed of light c, i.e., it is not a relativistic mass, the
relation is h = mv with m constant, and the two “energies” become
K (h) =
K
∗ (v)
Z h
1
0
m
Z v
=
0
h · dh =
1
1
khk2
h·h =
2m
2m
1
1
mv · dv = mv · v = m kvk2
2
2
As one can see, in this case the kinetic energy and co-energy are the same
since khk2 = m2 kvk2
This does not happen for relativistic masses where m = m(v(t)).
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
13 / 50
In an extended body composed by N masses mi the kinetic co-energy is
the sum of the kinetic co-energy of each mass
K ∗ (v) =
B. Bona (DAUIN)
1 N
∑ mi v i · v i
2 i=1
Lagrange
Semester 1, 2016-17
14 / 50
We consider the velocity v0i = ẋ0i with respect to R0 .
Each velocity i in R0 can be computed from the general relation
0
0
ẋ0i (t) = ω 001 (t) × ρ 0i (t) + R01 ẋ1i (t) + ḋ1 (t) = ω 001 (t) × ρ 0 (t) + ḋ1 (t)
where the term R01 ẋi (t) is zero, since the point-masses are fixed with
respect to the body-frame, i.e., ẋ1i (t) = 0.
Now we consider a purely translatory motion and then a purely rotational
motion.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
15 / 50
Translational motion
If the motion is purely translational all point masses have the same linear
velocity v0 with respect to R0
0
ẋ0i (t) = ḋ1 (t) ≡ v0 (t) ∀i
then
N
2 1
1
1
1
K ∗ = v0 · v0 ∑ mi = mtot v0 · v0 = mtot v0 = (v0 )T (mtot I)v0
2
2
2
2
i=1
where the mass mtot is the total body mass.
The kinetic co-energy is equivalent to that of one particle with total mass
mtot with the translational velocity v0 .
The total mass mtot can be ideally concentrated in the body
center-of-mass C , whose position is xc
xc mtot = ∑ xi mi
→
i
B. Bona (DAUIN)
Lagrange
xc =
1
xi m i
mtot ∑
i
Semester 1, 2016-17
16 / 50
Since the velocity is equal for all points of the body, v0 is also the velocity
of the center-of-mass C ; if we use the symbol v0c ≡ v0 for this velocity, we
can write
2 1
1
1
K ∗ = mtot v0c · v0c = mtot v0c = (v0c )T (mtot I)v0c
2
2
2
that gives the usual rule: “the kinetic energy is half the product of the
total mass for the total velocity squared.”
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
17 / 50
Rotational motion
If the motion is purely rotational, then
ẋ0i (t) = ω 001 (t) × xbi
i.e., vi = ω 0 × xi
where ω 001 ≡ ω 0 is the total angular velocity and xi is the position of the
i-th mass in R0 .
Considering all masses
K∗=
1 N
∑ mi (ω 0 × xi ) · (ω 0 × xi )
2 i=1
since
a · (b × c) = b · (c × a)
and assuming
a ≡ (ω 0 × xi ),
b ≡ ω 0,
c ≡ xi
we obtain
1 N
1
K = ∑ mi ω 0 · xi × (ω 0 × xi ) = ω 0 ·
2 i=1
2
∗
B. Bona (DAUIN)
Lagrange
!
N
∑ mi xi × (ω
0
× xi )
i=1
Semester 1, 2016-17
18 / 50
The previous relation is equivalent to
1
K = ω0 ·
2
∗
N
∑ hi
i=1
!
=
1 0
ω · h0
2
where h0 is the total angular momentum with respect to the origin O of
the reference frame R0 .
Since h0 = Γ0 ω 0 , we have
K∗=
1 0 T
(ω ) Γ0 ω 0
2
Notice the similarity:
1 0 T
(v ) (mtot I)v0c pure translation
2 c
∗ = 1 (ω 0 )T Γ ω 0
pure rotation
Krot
0
2
∗ =
Ktrasl
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
19 / 50
Total kinetic co-energy
Therefore, the total kinetic co-energy is
∗
∗
K ∗ = Ktrasl
+ Krot
=
o
1n 0 T
(vc ) (mtot I)v0c + (ω 0 )T Γ0 ω 0
2
This is a well known result, that can be expressed in words as:
the total kinetic co-energy of a body is the sum of the translational
kinetic co-energy of the center of mass plus the rotational kinetic
co-energy around the center of mass.
This relation is valid also for extended bodies.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
20 / 50
Generalized coordinates
Considering the generalized coordinates q(t) and velocities q̇(t) and the
Jacobians
vc = JL (q)q̇ or ω = JA (q)q̇
we obtain
K ∗ (q̇, q) =
i
1h T T
q̇ JL (mI)JL q̇ + q̇T JT
Γ
J
q̇
A c A
2
and
i
1 h
1
T
K ∗ (q̇, q) = q̇T JT
(mI)J
+
J
Γ
J
q̇ = q̇T Γtot q̇
c
L
A
L
A
2
2
where
T
Γtot = JT
L (mI)JL + JA Γc JA
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
21 / 50
Potential energy
Potential energy is a form of energy that depends only on position; two
types of position-related energies exist.
One is due to the gravitational field,
the other is the energy stored in the elastic components of the
body, that accumulate energy under the effects of deformation.
Since in our approach the considered bodied are rigid, the elastic parts are
external to the bodies and are represented by ideal springs that connect
various parts of the mechanical system.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
22 / 50
A potential function P(x), is a scalar function that depends only on the
T
position x = x y z
A force f is said to be conservative when it is the negative gradient of
P(r)
T
∂ P(x) ∂ P(x) ∂ P(x)
f(x) = −∇P(x) = −
∂x
∂y
∂z
If a potential function exists, it is called potential energy of the system
and it is unique apart from an additive constant.
This implies that the effects on the body dynamics depend only from the
potential energy variation, and not on its absolute value.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
23 / 50
Gravitational energy
An example of conservative force field is the gravitational field around the
Earth. The potential field produces the so-called weight forces.
The potential energy due to a gravitational field and associated to a
generic mass m is given by the following relation:
Pg = −mg · x0c
where g is the local gravitational acceleration vector and x0c is the body
center-of-mass position vector with respect to a plane going through the
origin of R0 and orthogonal to g, that provides the conventional zero value
of potential energy (zero potential energy plane) as shown in Figure.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
24 / 50
Figure: The potential energy due to the gravitational field.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
25 / 50
Elastic energy
Another force field is related to potential energy, that due to elastic
elements: these elements represent the abstract model of a proportional
relation between displacement and force.
If we assume a one-dimensional linear spring, the relation between the
applied force f and the linear elongation e from the rest position of the
spring is
f = ke e
If we assume a one-dimensional torsional or torsion spring we can write a
relation between the applied torque τ and the resulting angular
deformation δ from the rest position of the spring
τ = ke0 δ
ke and ke0 are the so-called elastic constants of the springs.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
26 / 50
Figure: A one dimensional linear spring. The rest length of the spring is x0 , and e
is the extension/compression occurring when the force f is applied.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
27 / 50
The potential energy is the integral of the virtual work performed by the
spring deformation
P(e) =
Z e
f · de
or
0
P(δ ) =
Z δ
τ · dδ
0
We can define also in this case the potential co-energies, that are
∗
P (f) =
Z f
e · df
or
0
∗
P (τ) =
Z τ
δ · dτ
0
the relation between P ∗ (f) and P(e) is is given by the Legendre
transformation
P ∗ (f) = f · e − P(e)
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
28 / 50
A nonlinear spring: the relation between f(t) and e is nonlinear, but the
relation f · e = P(e) + P ∗ (f) holds.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
29 / 50
When the elastic elements are linear with constant ke , the potential energy
and co-energy are given by
1
1
P(e) = eT (ke I)e = ke kek2
2
2
and
1
1
kfk2
P ∗ (f) = f T (ke I)−1 f =
2
2ke
When torsion springs with constant ke0 are considered, the potential energy
and co-energy are given by
1
1
P(δ ) = δ T (ke0 I)δ = ke0 kδ k2
2
2
and
1
1
P ∗ (τ) = τ T (ke0 I)−1 τ = 0 kτk2
2
2ke
In linear case, energies and co-energies are equal
P(e) = P ∗ (f)
B. Bona (DAUIN)
and P(δ ) = P ∗ (τ)
Lagrange
Semester 1, 2016-17
30 / 50
If the elastic constants are different along the three directions, a more
general relation applies
1
P(e) = eT Ke e;
2
1
P ∗ (f) = f T K−1
e f
2
and
1
1
P(δ ) = δ T K0e δ ; P ∗ (τ) = τ T (K0e )−1 τ
2
2
0 , k 0 , k 0 ) are the elastic
where Ke = diag(ke1 , ke2 , ke3 ) e K0e = diag(ke1
e2 e3
constant matrices along the three dimensional axes.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
31 / 50
Generalized forces in holonomic systems
The forces f i acting on the i-th mass can be classified according to three
groups:
N 000 constraint forces f vi due to constraint reactions.
N 00 conservative forces f ci due to conservative fields.
N 0 non conservative forces f nc
i .
The total force is the sum of these three types of forces
N0
f=
i=1
B. Bona (DAUIN)
N 00
N 000
c
v
∑ f nc
i + ∑ fi + ∑ fi
i=1
Lagrange
i=1
Semester 1, 2016-17
32 / 50
Constraint forces
The virtual displacements δ xi are always tangent to the constraints, while
the constraint forces f vi are always orthogonal to the constraints; from this
assumption it follows that
f vi · δ xi = 0
Therefore the work done by the constraint forces is zero (the forces “do
not work”)
δW =
v
N 000
∑ f vi · δ xi = 0.
i=1
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
33 / 50
Conservative forces
The N 00 conservative forces do a work that results
δW c =
N 00
N 00
∑ f ci · δ xi = − ∑ ∇Pi · δ xi =
i=1
i=1
"
" 00
#
#
N
n
∂ xi
∂ xi
− ∑ ∇Pi · ∑
δ qj = ∑ ∑ −∇Pi ·
δ qj
∂ qj
j=1 ∂ qj
i=1
j=1 i=1
|
{z
}
N 00
n
Fjc
This last expression highlights the so called generalized conservative
forces Fjc
The virtual work can be expressed as a function of the generalized
coordinates qj :
δW =
c
B. Bona (DAUIN)
N 00
n
i=1
j=1
∑ f ci · δ xi = ∑ Fjc δ qj = F c · δ q
Lagrange
Semester 1, 2016-17
34 / 50
Non conservative forces
The N 0 non conservative forces f nc
i do a work equal to
"
" 0
#
#
N0
n
N
N0
n
∂ xi
nc
nc ∂ xi
nc
nc
δ qj
δ W = ∑ f i · δ xi = ∑ f i · ∑
δ qj = ∑ ∑ f i ·
∂ qj
i=1
j=1 ∂ qj
i=1
j=1 i=1
|
{z
}
Fjnc
This last expression highlights the so called generalized non
conservative forces Fjnc and allows to transform the virtual work from a
function of the positions x to a function of the generalized coordinates qj :
δ W nc =
N 00
i=1
B. Bona (DAUIN)
n
∑ f nc
i · δ xi =
∑ Fjnc δ qj = F nc · δ q
j=1
Lagrange
Semester 1, 2016-17
35 / 50
In conclusion, only two types of forces will do work in a system subject to
holonomic constraints
the j-th generalized conservative forces:
Fjc (q)
N 00
= − ∑ ∇Pi ·
i=1
∂ xi
∂ qj
the j-th generalized non conservative forces:
Fjnc (q)
N0
=
∂ xi
∑ f nc
i ·
∂ qj
i=1
The generalized force, being the result of a scalar product, will be itself a
scalar quantity.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
36 / 50
In case of torques acting on the system, the generalized forces due to them
will give origin to the following generalized torques
Tj c =
N 00
∑ −∇Pi ·
i=1
∂ αi
;
∂ qj
Tj nc =
N0
∂ αi
∑ τ nc
i ·
∂ qj
i=1
The symbol used to identify both the generalized forces and the
generalized torques will be F .
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
37 / 50
Lagrange equations with holonomic constraints
In a multi-body system subject to holonomic constraints, the formulation
of the Lagrange equations may take different forms.
From the knowledge of the total co-energy of the system
K ∗ (q, q̇) =
N
∑ K`∗ (q, q̇)
`=1
one derives the Lagrange equations: they are a set of n equations (one for
each generalized coordinates qi ) defined as
d ∂K ∗
∂K ∗
−
= Fi
i = 1, . . . , n
dt
∂ q̇i
∂ qi
where Fi = Fic + Finc is the i-th generalized force, with a positive sign if
applied by the external environment to the body, or a negative sign if
applied by the body to the external environment.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
38 / 50
Since the conservative forces due to the gravitational field are the negative
of the gradient of the potential, we can move to the left hand part of the
equation, resulting in
" 0
#
N
∂ xk
d ∂K ∗
∂K ∗
+ ∑ ∇Pk ·
= Finc
−
dt
∂ q̇i
∂ qi
∂
q
i
k=1
∂P
; therefore
∂ qi
d ∂K ∗
∂K ∗ ∂P
−
−
= Finc
dt
∂ q̇i
∂ qi
∂ qi
The term inside the square bracket is equal to
Moreover P does not depend on q̇i , so one can write
∂P
=0
∂ q̇i
and one obtains the most common form of the Lagrange equations
d ∂K ∗ ∂P
∂K ∗ ∂P
−
−
−
= Finc
i = 1, . . . , n
dt
∂ q̇i
∂ q̇i
∂ qi
∂ qi
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
39 / 50
Lagrange state function
The Lagrange (state) function L is defined as the difference between
the total kinetic co-energy K ∗ and the total potential energy P of he
system
L (q, q̇) = K ∗ (q, q̇) − P(q)
We can write n differential equations
d ∂ L (q, q̇)
∂ L (q, q̇)
−
= Finc (q)
dt
∂ q̇i
∂ qi
i = 1, . . . , n
each one relative to the i-th generalized coordinate
∂L
The term
is the generalized momentum and is usually indicated by
∂ q̇i
the symbol µi ; the vector of generalized momenta is indicated by µ(q(t)).
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
40 / 50
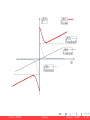
Dissipative and friction forces
The friction phenomena involve energy dissipated by the body as heat;
they are due to complex interaction between solid/solid or solid/fluid
surfaces; tribology is the science that studies the friction forces.
If we keep the friction or other dissipative forces fi fric separate from the
other non conservative forces, the Lagrange equation becomes:
d ∂L
∂L
= Fi − fi fric
−
dt ∂ q̇i
∂ qi
We can approximately describe the friction force fi fric as a nonlinear
function of the relative velocity v between the two contact surfaces of the
involved bodies.
We can model the total friction force as in Figure and write
fric
fric
fric
fric
ftotal
= fstiction
+ fcoulomb
+ fviscous
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
41 / 50
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
42 / 50
While stiction and Coulomb friction must be explicitly introduced as
non-conservative forces, it is a common assumption to express the viscous
dissipative phenomenon as the derivative of a dissipation function, also
called Rayleigh function, given by:
Di (q̇) =
1 T
1
q̇ (βi I)q̇ = βi kq̇k2
2
2
where the coefficient βi is the viscous friction coefficient, and kq̇k is the
norm of the relative velocity between the moving body and the surface
responsible of the viscous friction effect.
This quadratic expression is NOT a dissipation “energy”, but only a
conventional way to introduce it in the Lagrange equation, as follows
d ∂L
∂ L ∂ Di
+
= Fi i = 1, . . . , n
−
dt ∂ q̇i
∂ qi
∂ q̇i
Now the term Fi includes only the remaining non conservative forces
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
43 / 50
Summary
Find the k = 1, . . . , N rigid bodies composing the system and compute
the n degrees-of-freedom.
If necessary, define the various body frames Rk
Define a set of complete and independent generalized coordinates
qi (t), i = 1, . . . , n ≤ 6N
Compute the position vectors of each center-of mass
xk (q(t)), k = 1, . . . , N
Compute the linear velocity vectors of each center-of mass
vc,k (q(t), q̇(t)) and the angular velocities vectors ω k (q(t), q̇(t)) of
each body
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
44 / 50
Energy computation
Compute the kinetic co-energy Kk∗ of each k-th rigid body with mass
mk and inertia matrix (wrt the center-of-mass) Γk as
2 1
1
Kk∗ = mk vc,k + ω T
Γk ω k
2
2 k
Set the local gravity acceleration vector g and represent it in R0
Localize the Ne elastic energy storage elements and model them with
“ideal springs” with elastic constants k` , ` = 1, . . . , Ne
Compute the gravitational potential energy Pg ,k and the elastic
energy Pe,` as
Pg ,k = −mk gT pk
1
Pe,` = k` kek2
2
where e is the elongation (positive or negative) of the spring.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
45 / 50
Lagrangian function
Compute the total energies
K ∗ (q, q̇) =
N
∑ Kk∗
P(q) =
k=1
N
Ne
k=1
`=1
∑ Pg ,k + ∑ Pe,`
Compute the Lagrange function of the system L = K ∗ − P
Compute the generalized forces Fi
Write the n Lagrange equations
d ∂L
∂L
−
= Fi
i = 1, . . . , n
dt ∂ q̇i
∂ qi
i.e.,
d
dt
B. Bona (DAUIN)
∂K ∗
∂ q̇i
−
∂K ∗ ∂P
+
= Fi
∂ qi
∂ qi
Lagrange
i = 1, . . . , n
Semester 1, 2016-17
46 / 50
Lagrange equations
If there are linear dissipative elements, model them with a linear
dashpot, having friction coefficient βi .
1 2
Compute the dissipative function Di = βi vf ,i , where vf ,i is the
2
velocity associated to the friction producing element.
Upgrade the Lagrange equations as follows
d ∂K ∗
∂K ∗ ∂P ∂D
−
+
+
= Fi
i = 1, . . . , n
dt
∂ q̇i
∂ qi
∂ qi
∂ q̇i
When nonlinear elastic or friction elements are present, one should directly
introduce the resulting nonlinear elastic or friction forces at the second
term of the Lagrange equations.
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
47 / 50
Characterization of the Lagrange equations
The Lagrange approach generates n differential equations
d
dt
∂L
∂ q̇i
−
∂L
= Fi
∂ qi
i = 1, . . . , n
Collecting the n equations in one vector equation one obtains
d ∂L
∂L ∂D
−
+
=F
dt ∂ q̇
∂q
∂ q̇
If the equations are linear (or if we consider small perturbations around
some equilibrium point), we will have a general formulation expressed as a
second order differential vector equation
A1 q̈(t) + A2 q̇(t) + A3 q(t) = F
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
48 / 50
The linear equations can be rewritten as
Mq̈(t) + (D + G)q̇(t) + (K + H)q(t) = F
where
M = MT
is the mass or inertia matrix
positive definite, symmetric
D = DT
is the viscous damping matrix
symmetric
G = −GT
is the gyroscopic matrix
skew-symmetric
K = KT
is the stiffness (elasticity) matrix
symmetric
H = −HT is the circulatory matrix (constrained damping)
skew-symmetric
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
49 / 50
Lagrangian systems are holonomic systems where the forces are solely
due to generalized potential functions P(q, q̇),
Hamiltonian systems are those where the kinetic co-energy and the
potential energy explicitly depend on time
K ∗ = K ∗ (q, q̇, t)
and P = P(q, q̇, t)
... or, if you prefer the Wikipedia definition ...
A Lagrangian system is a pair (Y , L ) of a smooth fiber bundle Y → X
and a Lagrangian density L which yields the Euler–Lagrange differential
operator acting on sections of Y → X .
B. Bona (DAUIN)
Lagrange
Semester 1, 2016-17
50 / 50