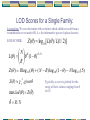Download Linkage Analysis: An Application of the Likelihood Ratio Test

Linkage Analysis: An Application of
the Likelihood Ratio Test
by Debbie Goldwasser
STAT600
November 8,2004
Topics for Discussion
Mendel’s Contribution to the Understanding
the Distribution of Genetic Material in Genetic
Crosses
What is the Goal of Linkage Analysis?
Why is a Likelihood Approach Appropriate?
Optimal?
How is Linkage Analysis Performed?
Abraham Wald’s Contribution to the
Optimization of Linkage Analysis Methods
Mendel: Brief Biography
Gregor Johann Mendel was born on July 22, 1822, in Heinzendorf,
Austria
The only son of a peasant farmer, his talents were recognized and
he attended the Olmutz Philosophical Institute as a young man
At age 21, Mendel entered the Augustinian monastery of St.
Thomas in Brunn, Austria, a site of impressive learning in many
areas of study
It was as a monk that Mendel developed an interest in the natural
sciences and gained recognition as a particularly well-received
teacher among his students
Published his landmark paper “Experiments in Plant
Hybridization” in 1865, in which he laid the experimental
foundation for the laws of independent assortment and the law of
segregation
After Mendel’s death in 1882, his work was rediscovered in 1902,
after which his ideas gained widespread recognition for their
relevance in explaining basic mechanisms of heredity.
Mendel and His Peas: The Law of
Segregation
Isolated pure breeds of plants with complementary traits then
crossed them to generate hybrids.
Defines “Dominant” and “Recessive” properties: dominant
properties constitute the entire character of the hybrid whereas
recessive properties are lost in the hybrid generation (i.e. Axa -A)
Crossed hybrids and found a ratio of 3:1 between dominant and
recessive traits (I.e. (3:1 A:a)
Key insight lie in Mendel’s ability to distinguish between dominant
forms of the hybrid cross. The ratio of variant dominant forms to
invariant dominant forms is 2:1 (Aa is Aa OR A in a ratio of 2:1)
Therefore he concluded that the ratio of peas resulting form the
hybrid cross has a true ratio of 1:2:1 (A:Aa:a)
These findings eventually led to the law of segregation which in
the year 2004 states that “diploid organisms possess genes in
pairs, and only one member of this pair is transmitted to each
offspring”.
Mendel and His Peas: The Law of
Independent Assortment
Next, Mendel looked at hybrid crosses from doubly
constant multiple traits (i.e. AbXaB)
Again, he defines the recessive properties as those that are
lost in the hybrid generation (lowercase letters)
The phenotypic ratio resulting from the hybrid cross is
9:3:3:1 for combinations of traits (AB:Ab:aB:ab)
Again, Mendel distinguished these offspring by their ability
to generate variant forms in order to find a true ratio of
(AB,Ab,ABb,AaB,AaBb,Aab,aBb,aB,ab) among the hybrids
to be 1:1:2:2:4:2:2:1:1
The law of independent assortment in the year 2004 states
that alleles at different loci segregate independently of each
other.
Relevance of Mendel’s Findings
Mendel’s findings form the basis for the study of genetics. It has
been proved that genes, in fact, do lie on chromosomes, of which
we receive a full set from both of our parents, resulting in a total
of two copies each. In the parent generation, unlinked genes
segregate independently of each other during meiosis and gamete
formation.
We can model the distribution of genes transmitted to offspring as
a series of Bernoulli trials. Each copy of a gene is transmitted with
probability ½
The law of independent assortment is the null hypothesis we will
test in linkage analysis. We will thus test the assumption that
neutral genetic material and a disease gene segregate
independently. If we suspect that a particular gene and disease
trait do not segregate independently, then we refer to them as
“linked”
A likelihood approach is used because the null hypothesis is a
fixed parameter.
The Law of Likelihood:
As quoted by Royall in “On the Probability of Observing
Misleading Statistical Evidence”: Hacking (1965)
defines the law of likelihood:
If one hypothesis, H1, implies that a random variable X takes the
value x with probability f1(x), while another hypothesis, H2,
implies that the probability is f2(x), then the observation X=x is
evidence supporting H1 over H2 if f1(x) > f2(x), measures the
strength of that evidence.
Define : LikelihoodRatio  f ( x |  1) / f ( x |  2)
A Neyman-Pearson approach asks, for a given hypotheses, how
likely is it that this data may have occurred?
An evidential likelihood approach asks, given the data, which of
my hypotheses best explains the data?
The likelihood ratio test can favor results
that the Neyman-Pearson test would
reject
Case Example: Let the critical value for the likelihood ratio = R.
H 1 : X  N ( ,  1)
H 2 : X  N ( ,  1   )
Suppose :   .05, N  30, observed X   1  1.65
Pr[ X   1  2 | N ( ,  1)]  1  
Pr[ X   1  2 | N ( ,  1   )] / Pr[ X   1  2 | N ( , 1)]  1 / R
The Universal Bound Links NeymanPearson Results with Likelihood Ratio
Tests
Pr(Misleading Evidence) + Pr(Weak Evidence) +Pr(Strong Evidence)=1
Define : Likelihood Ratio  f ( x |  1) / f ( x |  2)
  Pr[ rejectH1 | f 1( x |  1)true]
  Pr[ f ( x |  2) / f ( x |  1)  R) | f ( x |  1)]
   f ( x |  1)x
Domain : {x : f ( x |  2) / f ( x |  1)  R )}  {x : f ( x |  2)  Rf ( x |  1)}
 {x : f ( x |  1)  (1 / R ) f ( x |  2)
   f ( x |  1)x   (1 / R) f ( x |  2)x  1 / R
Conclusion: The Probability of Misleading Evidence is Bounded by 1/R
where R is the selected critical value for the likelihood test. As the sample
size becomes large the Pr(Misleading Evidence)  ((2 ln k )1 / 2)
Linkage Analysis: Intuitive Case Example
of Linkage:
Dd
1
2
Dd
dd
3
dd
4
5
6
7
8
9
Dd Dd
dd
dd
Dd
Dd
dd
10
dd
Suppose Children 2,5,6,9,10 have the disease and children 1,3,4,7,8 do
not. Intuitively conclude that Gene D is strongly related to the disease.
Linkage Analysis: Intuitive Case Example
of Non-Linkage:
Ff
ff
1
2
3
4
5
6
7
8
9
10
Ff
ff
Ff
Ff
ff
ff
Ff
Ff
ff
ff
Suppose Children 1,3,5,7,9 have the disease and children 2,4,6,8,10 do not.
Intuitively conclude that gene F is not related to the disease.
Mathematical Model: Key Features
Case: We have identified a disease that we are certain has a genetic
component. Therefore, we assume that a gene or genes relating to the
disease exist. Therefore, it or they must be located on one of the 23
chromosomes. Our job is to find them!
Linkage analysis entails testing the hypothesis that an unknown disease
gene is at a near position to a known piece of genetic material by looking at
the segregation ratio from the children.
Alternative Hypothesis (Linkage):
Gamete Probabilities:
D?
d?
D?
d?
D?
d?
F
f
F
f
f
F
(1   ) / 2
Null Hypothesis (Independence):
F
D?
d?
f
(1   ) / 2
 /2
 /2
Gamete Probabilities:
F
F
f
D?
1/ 4
f
d?
1/ 4
D?
1/ 4
d?
1/ 4
LOD Scores for a Single Family:
Assumption: We can determine with certainty which children result from a
recombination event under H1 (i.e. the informative parent is phase-known)
LOD SCORE:
Z ( )  log 10 [ L( ) / L(1 / 2)]
N R
L( )    (1   ) R  N
R 
Z ( )  R log 10 ( )  ( N  R) log 10 (1   )  N log 10 (.5)
Z ( )   1 , given
2
max lod ( )  Z (ˆ)
ˆ  R / N
Typically, a curve is plotted for the
range of theta values ranging from 0
to 0.5.
Why the Computation of LOD Scores is
More Complicated in Practice
• The sample size for a particular family is too small to
achieve significance from a single family. (i.e. probability of
3 Heads in a row is 1/8). N is constrained by the number of
children in a given family
• A simple way of combining multiple data sets is given
below. However, this statistic is not readily interpretable
for several reasons:
•Data is not distributed i.i.d. because family/pedigree
data comes in a variety of sizes.
•The phase of the data for a set of parents is not always
known. Oftentimes, this depends on gaining extended
pedigree information (i.e. grandparents), which is not
always available
K
Z ( )   Ri log 10 ( )  ( N i  Ri ) log 10 (1   )  N i log 10 (.5)
i 1
Abraham Wald: Brief
Biography
•Born into a Jewish intellectual family in Hungary in 1902, Wald was home-schooled
through primary and secondary schools by his parents
•Attended the University of Cluj (Romania) and demonstrated outstanding ability in
mathematics
•Continued his studies at the University of Vienna with Karl Menger and was
awarded his doctorate in 1931.
•Continued his research while serving as a mathematics tutor to the wealthy Karl
Schlesinger, a leading banker and economist. Wald developed an interest in
economics and econometrics
•After the Nazi occupation of Austria in 1938, Wald’s position became tenuous, so he
emigrated to the United States to become a Fellow of the Carnegie corporation
studying statistics at Columbia University under Hotelling
•Made key contributions in the area of decision theory, time series, sequential
analysis.
Abraham Wald’s Theory on
Sequential Probability Testing
Wald: “By a sequential test of a statistical hypothesis is meant any
statistical test procedure which gives a specific rule at any stage of the
experiment for making one of the following three decisions: (1) to accept
the hypothesis being tested (null hypothesis) (2) to reject the null
hypothesis, (3) to continue the experiment by making an additional
observations”.
Wald invented the topic of sequential analysis in response to the demand
for more efficient methods (i.e. reduced cost) of industrial quality control
during World War II.
Decision Rule in Wald’s Sequential
Probability Testing Scheme
g 0 m  g 0 p 0 m ( x1 ,..., x m ) /( g 0 p 0 m ( x1 ,..., x m )  g1 p1m ( x1 ,..., x m ))
g1m  g1 p1m ( x1 ,..., x m ) /( g 0 p 0 m ( x1 ,..., x m )  g1 p1m ( x1 ,..., x m ))
Choose : 1  d 0  1 / 2
Choose : 1  d1  1 / 2
g1m  g1 p1m /( g 0 p 0 m  g1 p1m )  d1
g 0 m  g 0 p 0 m /( g 0 p 0 m  g1 p1m )  d 0
Suppose : g1m  g 0 m  d1  d 0  1  d1  d 0 : Contradiction
p1m / p 0 m  ( g 0 / g1 ) * d1 /(1  d1 )
p1m / p 0 m  ( g 0 / g1 ) * (1  d 0 ) / d 0
AcceptH1 : p1m / p 0 m  A
AcceptH 0 : p1m / p 0 m  B
Re peat : B  p1m / p 0 m  A
Sequential Probability Testing
and Linkage Analysis
Wald claims that his test is most efficient when used for testing a
simple hypothesis against a single alternative. S and S* are two
different methods of testing with the same strength (Type I and
Type II Error rates).
Efficiency:
Max[ E0 (n | S*), E1 (n | S*)]
Max[ E0 (n | S ), E1 (n | S )]
It is desirable when searching for potential biomarkers to minimize
the time to a decision, given the large amount of potential gene
targets.
Mendel’s youthful
reflections…
Yes, his laurels shall never fade,
though time shall suck down by its vortex
Whole generations into the abyss,
Though naught but moss grow fragments
Shall remain of the epoch
In which the genius appeared…
May the might of destiny grant me
The supreme ecstasy of earthly joy
The highest goal of earthly destiny
That of seeing, when I arise from the tomb,
My art thriving peacefully
Among those who are to come after me.
Gregor Mendel, circa 1830-1840
References
Hodge, Susan E. (Spring 2004) Course Notes, “Theoretical
Genetic Modeling” Columbia University
Morton, Newton E.,(1955) Sequential Tests for the Detection of
Linkage, American Journal of Human Genetics 7:277-318
Wald, Abraham, Sequential Tests of Statistical Hypotheses
Annals of Mathematical Statistics 1945; 6: 117–186
Mendel, Gregor, Experiments in Plant Hybridization,
Proceedings of the Natural History Society,1865;
Sham, Pak (1998): Statistics in Human Genetics, Arnold
Publishers (London)
Royall, Richard, On the Probability of Observing Misleading
Statistical Evidence, Journal of the American Statistical
Association; 2000; 95:760-780.