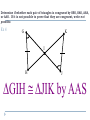Download Applying Triangle Sum Properties

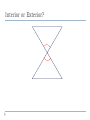
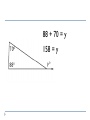
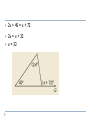
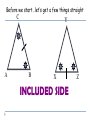
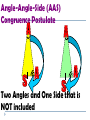
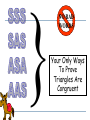
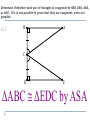
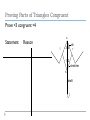
Applying Triangle Sum Properties
Section 4.1
Triangles

Triangles are polygons with three sides.

There are several types of triangle:







Scalene
Isosceles
Equilateral
Equiangular
Obtuse
Acute
Right
Scalene Triangles

Scalene triangles do not have any congruent sides.

In other words, no side has the same length.
6cm
3cm
8cm
Isosceles Triangle

A triangle with 2 congruent sides.

2 sides of the triangle will have the same length.

2 of the angles will also have the same angle measure.
Equilateral Triangles

All sides have the same length
Equiangular Triangles

All angles have the same angle measure.
Acute Triangle

All angles are acute angles.
Right Triangle

Will have one right angle.
Obtuse Angle

Will have one obtuse angle.
Exterior Angles vs. Interior Angles

Exterior Angles are angles that are on the outside of a
figure.

Interior Angles are angles on the inside of a figure.
Interior or Exterior?
Interior or Exterior?
Interior or Exterior?
Triangle Sum Theorem (Postulate Sheet)

States that the sum of the interior angles is 180.

We will do algebraic problems using this theorem.
The sum of the
angles is 180, so
x + 3x + 56= 180
4x + 56= 180
4x = 124
x = 31
Find the Value for X
2x + 15
2x + 15 + 3x + 90 = 180
5x + 105 = 180
3x
5x = 75
x = 15
Corollary to the Triangle Sum Theorem
(Postulate Sheet)

Acute angles of a right triangle are complementary.
3x + 10
5x +16
Exterior Angle Sum Theorem

The measure of the exterior angle of a triangle is equal to
the sum of the non-adjacent interior angles of the triangle
88 + 70 = y
158 = y

2x + 40 = x + 72

2x = x + 32
x = 32

Find x and y
46
o
8x - 1
3x + 13
2y
o
4.1 Apply Congruence and Triangles
4.2 Prove Triangles Congruent by SSS, SAS
1.
2.
3.
Objectives:
To define congruent triangles
To write a congruent statement
To prove triangles congruent by SSS, SAS
Congruent Polygons
Congruent Triangles (CPCTC)
Two triangles are congruent triangles if
and only if the corresponding parts of those
congruent triangles are congruent.
Congruence Statement
When naming two congruent triangles, order is very
important.
Example
Which polygon is congruent to ABCDE?
ABCDE  -?-
Properties of Congruent Triangles
Example
What is the relationship
between C and F?
D
75
F
C
30
E
A
75
30
B
Third Angle Theorem
If two angles of one triangle are congruent to
two angles of another triangle, then the
third angles are also congruent.
Congruent Triangles
Checking to see if 3 pairs of corresponding
sides are congruent and then to see if 3 pairs
of corresponding angles are congruent makes
a total of SIX pairs of things, which is a lot!
Surely there’s a shorter way!
Congruence Shortcuts?

Will one pair of congruent sides be sufficient? One pair
of angles?
Congruence Shortcuts?

Will two congruent parts be sufficient?
Congruent Shortcuts?
Will three congruent parts be
sufficient?
 And if so….what three parts?

Section 4.3
Proving Triangles are Congruents by SSS
Draw any triangle using any 3 size lines


For me I use lines of 5, 4, and 3 cm’s.
Now use the same lengths and see if you can make a
different triangle.
53
3cm

5cm

3cm
90
53
4cm
5cm
Now
measure
both
triangles
angles
and
see what you get.
90
37
4cm
37
Are the following triangles congruent? Why?
10
6
6
6
6
a.
10
YES, all sides
are equal so SSS
9
10
8
10
b.
9
6
No, all sides
are not equal
8 ≠ 6, so fails
SSS
Use the SSS Congruence Postulate
Decide whether the congruence
statement is true.
Explain your reasoning.
KLM  NLM
SOLUTION
KL  NL
Given
KM  NM
Given
LM  LM
Reflexive Property
So, by the SSS Congruence Postulate,
KLM  NLM
4.4:Prove Triangles Congruent by SAS and
HL
Goal:Use sides and angles to prove
congruence.
Vocabulary


Leg of a right triangle: In a right triangle, a side adjacent to
the right angle is called a leg.
Hypotenuse:In a right triangle, the side opposite the right
angle is called the hypotenuse.
Hypotenuse
Leg
Before we start…let’s get a few things straight
C
A
Y
B
X
INCLUDED SIDE
Z
Angle-Side-Angle (ASA)
Congruence Postulate
Two angles and the INCLUDED side
Angle-Angle-Side (AAS)
Congruence Postulate
Two Angles and One Side that is
NOT included
}
NO BAD
WORDS
Your Only Ways
To Prove
Triangles Are
Congruent
Things you can mark on a triangle when they aren’t marked.
Overlapping sides are
congruent in each
triangle by the
REFLEXIVE property
Vertical
Angles are
congruent
Alt Int
Angles are
congruent
given
parallel lines
Ex 1
In ΔDEF and ΔLMN , D  N , DE  NL and
E  L. Write a congruence statement.
 DEF   NLM
Ex 2
What other pair of angles needs to be marked so
that the two triangles are congruent by AAS?
D
E  N
L
M
F
E
N
Ex 3
What other pair of angles needs to be marked so
that the two triangles are congruent by ASA?
D
D  L
L
M
F
E
N
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA,
or AAS. If it is not possible to prove that they are congruent, write not
possible.
Ex 4
G
K
I
H
J
ΔGIH  ΔJIK by AAS
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA,
or AAS. If it is not possible to prove that they are congruent, write not
possible.
Ex 5
B
A
C
D
E
ΔABC  ΔEDC by ASA
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA,
or AAS. If it is not possible to prove that they are congruent, write not
possible.
Ex 6
E
A
C
B
D
ΔACB  ΔECD by SAS
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA,
or AAS. If it is not possible to prove that they are congruent, write not
possible.
Ex 7
J
M
K
L
ΔJMK  ΔLKM by SAS or ASA
Determine if whether each pair of triangles is congruent by SSS, SAS, ASA,
or AAS. If it is not possible to prove that they are congruent, write not
possible.
Ex 8
J
T
K
L
V
Not possible
U
Postulate 20:Side-Angle-Side (SAS)
Congruence Postulate

If two sides and the included angle of one triangle are congruent to two
sides and the included angle of a second triangle, then the two triangles are
congruent.
If
then
Side RS  UV ,
Angle R  U , and
Side RT  UW ,
RST  UVW .
Example 1:Use the SAS Congruence Postulate

Write a proof.
Given
Prove
JN  LN , KN  MN
JKN  LMN
J
L
N
1
Statements
1. JN  LN ,
Reasons
1. Given
K
KN  MN
2. 1  2
2. Vertical Angles Theorem
3. JKN  LMN
3. SAS Congruence Postulate
2
M
Example 2:Use SAS and properties of shapes
In the diagram, ABCD is a rectangle.
What can you conclude about
By ABC
the Right
and Angles
CDA ? Congruence Theorem,
B  D. Opposite sides of a rectangle are congruent,
so AB  CD and BC  DA.
ABC and CDA are congruent by the SAS Congruence
Postulate.
Checkpoint
In the diagram, AB, CD, and EF pass
through the center M of the circle.
Prove that DMY  BMY .
Also, 1  2  3  4.
Statements
Reasons
1. 3  4
2. DM  BM
1. Given
2. Definition of a
3. MY  MY
4. DMY  BMY
3. Reflexive Property of
Congruence
4. SAS Congruence
Postulate
Checkpoint
In the diagram, AB, CD, and EF pass
through the center M of the circle.
What can you conclude about AC and
Also, 1  2  3  4.
BD ?
Because they are vertical angles,
AMC  BMD. All points on a circle are the
same distance from the center, so
AM  BM  CM  DM . By the SAS Congruence
Postulate, AMC  BMD. Corresponding parts
of congruent triangles are congruent, so you
know AC  BD.
Theorem 4.5:Hypotenuse-Leg Congruence
Theorem

If the hypotenuse and a leg of a right triangle
are congruent to the hypotenuse and a leg of a
second triangle, then the two triangles are
congruent.
Example 3:Use the Hypotenuse-Leg Theorem

Write a proof.
Given AC  EC ,
AB  BD,
ED  BD,
AC is a bisector of BD.
Prove ABC  EDC
Example 3:Use the Hypotenuse-Leg Theorem
Statements
H 1. AC  EC
2. AB  BD,
Reasons
1. Given
2. Given
ED  BD
3. B and D are 3. Definition of  lines
right angles.
4. ABC and EDC 4. Definition of a
are right triangles.
right triangle
5. AC is a bisector 5. Given
of BD.
Example 3:Use the Hypotenuse-Leg Theorem
Statements
L 6. BC  DC
Reasons
6. Definition of segment
bisector
7. ABC  EDC 7. HL Congruence
Theorem
Example 4:Choose a postulate or theorem
Gate The entrance to a ranch
has a rectangular gate as shown
in the diagram. You know that
AFC  EFC. What postulate
or theorem can you use to
conclude that ABC  EDC ?
Example 4:Choose a postulate or theorem
You are given that ABDE is a rectangle, so B and D
are right angles. Because opposite sides of a rectangle
are congruent, AB  DE. You are also given that
AFC  EFC , so AC  EC. The hypotenuse and a leg
of each triangle is congruent.
You can use the HL Congruence Theorem to conclude
that ABC  EDC.
Using Congruent Triangles: CPCTC
Academic Geometry
Proving Parts of Triangles Congruent
You know how to use SSS, SAS, ASA, and AAS to show that
the triangles are congruent.
Once you have triangles congruent, you can make
conclusions about their other parts because, by definition,
corresponding parts of congruent triangles are congruent.
Abbreviated CPCTC
Proving Parts of Triangles Congruent
In an umbrella frame, the stretchers are congruent and they open to angles of
equal measure.
Given SL congruent to SR
<1 congruent <2
Prove that the angles formed by the shaft
and the ribs are congruent
c
l
rib
3 4 r
1 2
stretcher
s
shaft
Proving Parts of Triangles Congruent
Prove <3 congruent <4
Statement
c
Reason
l
rib
3 4
r
1 2
stretcher
s
shaft
Proving Parts of Triangles Congruent
Given <Q congruent <R
<QPS congruent <RSP
p
Prove SQ congruent PR
Statements
q
Reasons
r
s
Proving Parts of Triangles Congruent
Given <DEG and < DEF are right angles.
<EDG congruent <EDF
Prove EF congruent EG
d
f
e
Statements
Reasons
g
4.7 Isosceles and Equilateral
Triangles
Chapter 4
Congruent Triangles
4.5 Isosceles and Equilateral Triangles
Isosceles Triangle:
Vertex Angle
Leg
Leg
Base Angles
Base
*The Base Angles are Congruent*
Isosceles Triangles

Theorem 4-3 Isosceles Triangle Theorem
If two sides of a triangle are congruent, then the angles opposite
those sides are congruent
B
<A = <C
A
C
Isosceles Triangles

Theorem 4-4
Converse of the Isosceles
Triangle Theorem
If two angles of a triangle are congruent, then the sides opposite
those angles are congruent
B
Given: <A = <C
Conclude: AB = CB
A
C
Isosceles Triangles

Theorem 4-5
The bisector of the vertex angle of an isosceles triangle is the
perpendicular bisector of the base
B
Given: <ABD = <CBD
Conclude: AD = DC and
BD is ┴ to AC
A
D
C
Equilateral Triangles

Corollary: Statement that immediately follows a theorem
Corollary to Theorem 4-3:
If a triangle is equilateral, then the triangle
is equiangular
Corollary to Theorem 4-4:
If a triangle is equiangular, then the triangle
is equilateral
Using Isosceles Triangle Theorems
Explain why ΔRST is isosceles.
T
U
Given: <R = <WVS,
VW = SW
Prove: ΔRST is isosceles
Statement
R
Reason
1. VW = SW
1. Given
2. m<WVS = m<S
2. Isosceles Triangle Thm.
3. m<R = m<WVS
3. Given
4. Transitive Property
4. m<S = m<R
5. ΔRST is isosceles 5. Def Isosceles Triangle
W
V
S
Using Algebra
Find the values of x and y:
M
ΔLMN is isosceles
m<L = m< N = 63
m<LM0 = y = m<NMO
63 + 63 + y + y = 180
126 + 2y = 180
- 126
-126
2y = 54
2
2
y = 27
y°
y° 27°
63°
x°
63°
L
27 + 63 + x = 180
90 + x = 180
-90
-90
x = 90
O
N
Landscaping
A landscaper uses rectangles and equilateral triangles for the path
around the hexagonal garden. Find the value of x.
x°