* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Proving the Vertical Angles Theorem - 3
Survey
Document related concepts
Rotation formalisms in three dimensions wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Integer triangle wikipedia , lookup
Line (geometry) wikipedia , lookup
Multilateration wikipedia , lookup
Rational trigonometry wikipedia , lookup
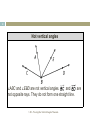
Noether's theorem wikipedia , lookup
Riemann–Roch theorem wikipedia , lookup
History of trigonometry wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Trigonometric functions wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Transcript
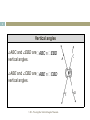
PROVING THE VERTICAL ANGLES THEOREM Adapted from Walch Education Key Concepts 2 Angles can be labeled with one point at the vertex, three points with the vertex point in the middle, or with numbers. If the vertex point serves as the vertex for more than one angle, three points or a number must be used to name the angle. 1.8.1: Proving the Vertical Angles Theorem Straight Angle 3 • Straight angles are straight lines. Straight angle Not a straight angle ∠BCD is a straight angle. Points ∠PQR is not a straight angle. B, C, and D lie on the same line. Points P, Q, and R do not lie on the same line. 1.8.1: Proving the Vertical Angles Theorem Adjacent Angles 4 • • Adjacent angles are angles that lie in the same plane and share a vertex and a common side. They have no common interior points. Nonadjacent angles have no common vertex or common side, or have shared interior points. 1.8.1: Proving the Vertical Angles Theorem 5 Adjacent angles ∠ABC is adjacent to ∠CBD. They share vertex B and . ∠ABC and ∠CBD have no common interior points. 1.8.1: Proving the Vertical Angles Theorem 6 Nonadjacent angles ∠ABE is not adjacent to ∠FCD. They do not have a common vertex. 1.8.1: Proving the Vertical Angles Theorem 7 Nonadjacent angles ∠PQS is not adjacent to ∠PQR. They share common interior points within ∠PQS. 1.8.1: Proving the Vertical Angles Theorem Linear pair 8 Linear pairs are pairs of adjacent angles whose nonshared sides form a straight angle Linear pair ∠ABC and ∠CBD are a linear pair. They are adjacent angles with non-shared sides, creating a straight angle. 1.8.1: Proving the Vertical Angles Theorem 9 Not a linear pair ∠ABE and ∠FCD are not a linear pair. They are not adjacent angles. 1.8.1: Proving the Vertical Angles Theorem Vertical Angles 10 • Vertical angles are nonadjacent angles formed by two pairs of opposite rays. Theorem Vertical Angles Theorem Vertical angles are congruent. 1.8.1: Proving the Vertical Angles Theorem 11 Vertical angles ∠ABC and ∠EBD are ÐABC @ ÐEBD vertical angles. ∠ABE and ∠CBD are ÐABE @ ÐCBD vertical angles. 1.8.1: Proving the Vertical Angles Theorem 12 Not vertical angles ∠ABC and ∠EBD are not vertical angles. and are not opposite rays. They do not form one straight line. 1.8.1: Proving the Vertical Angles Theorem Angle Addition Postulate 13 Postulate Angle Addition Postulate If D is in the interior of ∠ABC, then m∠ABD + m∠DBC = m∠ABC. If m∠ABD + m∠DBC = m∠ABC, then D is in the interior of ∠ABC. 1.8.1: Proving the Vertical Angles Theorem Key Concepts 14 • • • The Angle Addition Postulate means that the measure of the larger angle is made up of the sum of the two smaller angles inside it. Supplementary angles are two angles whose sum is 180º. Supplementary angles can form a linear pair or be nonadjacent. 1.8.1: Proving the Vertical Angles Theorem Supplementary Angles 15 • In the diagram below, the angles form a linear pair. m∠ABD + m∠DBC = 180 1.8.1: Proving the Vertical Angles Theorem Supplementary Angles 16 • A pair of supplementary angles that are nonadjacent. m∠PQR + m∠TUV = 180 1.8.1: Proving the Vertical Angles Theorem 17 Theorem Supplement Theorem If two angles form a linear pair, then they are supplementary. Theorem Angles supplementary to the same angle or to congruent angles are congruent. If and , then . 1.8.1: Proving the Vertical Angles Theorem Properties of Congruence 18 Theorem Congruence of angles is reflexive, symmetric, and transitive. • Reflexive Property: Ð1@ Ð1 • Symmetric Property: If Ð1@ Ð2, then Ð2 @ Ð1. • Transitive Property: If Ð1@ Ð2 and Ð2 @ Ð3, then Ð1@ Ð3 . 1.8.1: Proving the Vertical Angles Theorem Perpendicular Lines 19 • Perpendicular lines form four adjacent and congruent right angles. Theorem If two congruent angles form a linear pair, then they are right angles. If two angles are congruent and supplementary, then each angle is a right angle. 1.8.1: Proving the Vertical Angles Theorem Perpendicular Lines 20 • • • The symbol for writing perpendicular lines is is read as “is perpendicular to.” ^ , and Rays and segments can also be perpendicular. In a pair of perpendicular lines, rays, or segments, only one right angle box is needed to indicate perpendicular lines. 1.8.1: Proving the Vertical Angles Theorem Concepts, continued 21 • • Perpendicular bisectors are lines that intersect a segment at its midpoint at a right angle; they are perpendicular to the segment. Any point along the perpendicular bisector is equidistant from the endpoints of the segment that it bisects. 1.8.1: Proving the Vertical Angles Theorem 22 Theorem Perpendicular Bisector Theorem If a point lies on the perpendicular bisector of a segment, then that point is equidistant from the endpoints of the segment. If a point is equidistant from the endpoints of a segment, then the point lies on the perpendicular bisector of the segment. 1.8.1: Proving the Vertical Angles Theorem 23 Theorem If is the perpendicular bisector of AC, then DA = DC. If DA = DC, then is the perpendicular bisector of AC . 1.8.1: Proving the Vertical Angles Theorem Complementary Angles 24 • • Complementary angles are two angles whose sum is 90º. Complementary angles can form a right angle or be nonadjacent. 1.8.1: Proving the Vertical Angles Theorem 25 Complementary Angles mÐB + mÐE = 90 1.8.1: Proving the Vertical Angles Theorem Complementary Angles 26 • The diagram at right shows a pair of adjacent complementary angles labeled with numbers. mÐ1+ mÐ2 = 90 1.8.1: Proving the Vertical Angles Theorem 27 Theorem Complement Theorem If the non-shared sides of two adjacent angles form a right angle, then the angles are complementary. Angles complementary to the same angle or to congruent angles are congruent. 1.8.1: Proving the Vertical Angles Theorem Practice 28 Prove that vertical angles are congruent given a pair of intersecting lines, and . 1.8.1: Proving the Vertical Angles Theorem Draw a Diagram 29 1.8.1: Proving the Vertical Angles Theorem Supplement Theorem 30 Supplementary angles add up to 180º. mÐ1+ mÐ2 = 180 mÐ2 + mÐ3 = 180 1.8.1: Proving the Vertical Angles Theorem Use Substitution 31 Both expressions are equal to 180, so they are equal to each other. Rewrite the first equation, substituting m∠2 + m∠3 in for 180. m∠1 + m∠2 = m∠2 + m∠3 1.8.1: Proving the Vertical Angles Theorem Reflexive Property 32 m∠2 = m∠2 1.8.1: Proving the Vertical Angles Theorem Subtraction Property 33 Since m∠2 = m∠2, these measures can be subtracted out of the equation m∠1 + m∠2 = m∠2 + m∠3. This leaves m∠1 = m∠3. 1.8.1: Proving the Vertical Angles Theorem Definition of Congruence 34 Since m∠1 = m∠3, by the definition of congruence, Ð1@ Ð3. ∠1 and ∠3 are vertical angles and they are congruent. This proof also shows that angles supplementary to the same angle are congruent. 1.8.1: Proving the Vertical Angles Theorem Try this one… 35 In the diagram at right, is the perpendicular bisector of . If AD = 4x – 1 and DC = x + 11, what are the values of AD and DC? 1.8.1: Proving the Vertical Angles Theorem Thanks For Watching! Dr. Dambreville