Download 7 - Landerson.net

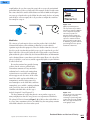
Back
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
CHAPTER 7
Rotational
Motion and the
Law of Gravity
PHYSICS IN ACTION
When riding this spinning amusement-park
ride, people feel as if a force is pressing
them against the padding on the inside walls
of the ride. However, it is actually inertia
that causes their bodies to press against the
padding. The inertia of their bodies tends to
maintain motion in a straight-line path,
while the walls of the ride exert a force on
their bodies that makes them follow a circular path. This chapter will discuss the
force that maintains circular motion and
other rotational-motion quantities.
•
How can you determine the riders’ average
linear speed or acceleration during the ride?
•
In what direction are the forces pushing or
pulling the riders?
CONCEPT REVIEW
Displacement (Section 2-1)
Velocity (Section 2-1)
Acceleration (Section 2-2)
Force (Section 4-1)
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Rotational Motion and the Law of Gravity
243
Back
7-1
Measuring rotational motion
7-1 SECTION OBJECTIVES
ROTATIONAL QUANTITIES
•
•
Relate radians to degrees.
•
Calculate angular speed or
angular acceleration.
•
Solve problems using the
kinematic equations for
rotational motion.
Figure 7-1
When an object spins, it is said to undergo rotational motion. Consider a
spinning Ferris wheel. The axis of rotation is the line about which the rotation
occurs. In this case, it is a line perpendicular to the side of the Ferris wheel and
passing through the wheel’s center. How can we measure the distance traveled
by an object on the edge of the Ferris wheel?
A point on an object that rotates about a single axis undergoes circular motion
around that axis. In other words, regardless of the shape of the object, any single
point on the object travels in a circle around the axis of rotation. It is difficult to
describe the motion of a point moving in a circle using only the linear quantities
introduced in Chapter 2 because the direction of motion in a circular path is
constantly changing. For this reason, circular motion is described in terms of the
angle through which the point on an object moves. When rotational motion is
described using angles, all points on a rigid rotating object, except the points on
the axis, move through the same angle during any time interval.
In Figure 7-1, a light bulb at a distance r from the center of a Ferris
wheel, like the one shown in Figure 7-2, moves about the axis in
a circle of radius r. In fact, every point on the wheel
undergoes circular motion about the center. To analyze such motion, it is convenient to set up a fixed
reference line. Let us assume that at time t = 0,
the bulb is on the reference line, as in Figure
7-1(a), and that a line is drawn from the
center of the wheel to the bulb. After a
time interval ∆t, the bulb advances to a
new position, as shown in Figure
7-1(b). In this time interval, the line
from the center to the bulb (depicted with a red line in both diagrams)
moved through the angle q with
respect to the reference line. Likewise, the bulb moved a distance s,
measured along the circumference
of the circle; s is the arc length.
A light bulb on a rotating Ferris
wheel (a) begins at a point along a
reference line and (b) moves
through an arc length s, and therefore through the angle q .
Any point on a Ferris wheel that spins about
a fixed axis undergoes circular motion.
Calculate angular displacement using the arc length
and the distance from the
axis of rotation.
rotational motion
motion of a body that spins
about an axis
Light
bulb
r
Reference
line
(a)
Light
bulb
θ
r
s
Reference
line
(b)
244
Chapter 7
Figure 7-2
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
Angles can be measured in radians
In the situations we have encountered so far, angles have been measured in
degrees. However, in science, angles are often measured in radians (rad) rather
than in degrees. Almost all of the equations used in this chapter and the next
require that angles be measured in radians. In Figure 7-1(b), when the arc
length, s, is equal to the length of the radius, r, the angle q swept by r is equal to
1 rad. In general, any angle q measured in radians is defined by the following:
radian
an angle whose arc length is
equal to its radius, which is
approximately equal to 57.3 °
s
q = 
r
The radian is a pure number, with no dimensions. Because q is the ratio of
an arc length (a distance) to the length of the radius (also a distance), the
units cancel and the abbreviation rad is substituted in their place.
When the bulb on the Ferris wheel moves through an angle of
120°
2π
360° (one revolution of the wheel), the arc length s is equal to the
135° 3π 3
4
circumference of the circle, or 2pr. Substituting this value for s
150° 5π
6
in the above equation gives the corresponding angle in radians.
s 2p r
q =  =  = 2p rad
r
r
180° π
y
90°
1
π
2
60°
1
π 45°
3 1
π 30°
4
1
π
6
0°
2π 360°
x
7π
Thus, 360° equals 2p rad, or one complete revolution. In
6
11π
5
other words, one revolution corresponds to an angle of approxi330°
6
210° 4π 4
7
π
π
mately 2(3.14) = 6.28 rad. Figure 7-3 depicts a circle marked with
3
4
5
315°
225°
π
3π
3
both radians and degrees.
2
300°
240°
270°
It follows that any angle in degrees can be converted to an angle in
radians by multiplying the angle measured in degrees by 2p/360°. In this
way, the degrees cancel out and the measurement is left in radians. The conFigure 7-3
Angular motion is measured in units
version relationship can be simplified as follows:
of radians. Because there are 2p
radians in a full circle, radians are
often expressed as a multiple of p.
p
q (rad) = q (deg)
180°
Radians and Arc Length
MATERIALS
✔ drawing compass
✔ paper
✔ thin wire
✔ wire cutters or scissors
Use the compass to draw a circle on a
sheet of paper, and mark the center point
of the circle. Measure the distance from
the center point to the outside of the circle. This is the radius of the circle. Using
the wire cutters, cut several pieces of wire
equal to the length of this radius. Bend the
pieces of wire, and lay them along the circle you drew with your compass. Approximately how many pieces of wire do you
Copyright © by Holt, Rinehart and Winston. All rights reserved.
use to go all the way around the circle?
Draw lines from the center of the circle to
each end of one of the wires. Note that
the angle between these two lines equals
1 rad. How many of these angles are there
in this circle? Draw a larger circle using
your compass. How many pieces of wire
(cut to the length of the radius) do you
use to go all the way around this circle?
Rotational Motion and the Law of Gravity
245
Back
Angular displacement describes how much an object has rotated
angular displacement
the angle through which a point,
line, or body is rotated in a specified direction and about a specified axis
Just as an angle in radians is the ratio of the arc length to the radius, the angular displacement traveled by the bulb on the Ferris wheel is the change in the
arc length, ∆s, divided by the distance of the bulb from the axis of rotation.
This relationship is depicted in Figure 7-4.
ANGULAR DISPLACEMENT
∆s
∆q = 
r
θ2
change in arc length
angular displacement (in radians) = 
distance from axis
θ1
Reference
line
Figure 7-4
A light bulb on a rotating Ferris
wheel rotates through an angular
displacement of ∆q = q2 − q1 .
For the purposes of this textbook, when a rotating object is viewed from
above, the arc length, s, is considered positive when the point rotates counterclockwise and negative when it rotates clockwise. In other words, ∆q is positive when the object rotates counterclockwise and negative when the object
rotates clockwise.
SAMPLE PROBLEM 7A
Angular displacement
PROBLEM
While riding on a carousel that is rotating clockwise, a child travels
through an arc length of 11.5 m. If the child’s angular displacement is
165, what is the radius of the carousel?
SOLUTION
Given:
Unknown:
∆q = −165°
r=?
∆s = −11.5 m
First, convert the angular displacement to radians using the relationship on
page 245.
p
p
∆q (rad) = ∆q(deg) = (−165°)
180°
180°
∆q (rad) = −2.88 rad
Use the angular displacement equation on this page. Rearrange to solve for r.
∆s
∆q = 
r
∆s −11.5 m
r =  = 
∆q −2.88 rad
r = 3.99 m
246
Chapter 7
CALCULATOR SOLUTION
Many calculators have a key labeled
DEG that converts from degrees to
radians.
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
PRACTICE 7A
Angular displacement
1. A girl sitting on a merry-go-round moves counterclockwise through an
arc length of 2.50 m. If the girl’s angular displacement is 1.67 rad, how
far is she from the center of the merry-go-round?
2. A beetle sits at the top of a bicycle wheel and flies away just before it
would be squashed. Assuming that the wheel turns clockwise, the beetle’s
angular displacement is p rad, which corresponds to an arc length of 1.2
m. What is the wheel’s radius?
p
3. A car on a Ferris wheel has an angular displacement of  rad, which cor4
responds to an arc length of 29.8 m. What is the Ferris wheel’s radius?
4. Fill in the unknown quantities in the following table:
a.
∆q
∆s
r
? rad
+0.25 m
0.10 m
?
−4.2 m
+2.6 m
8.5 m
0.75 m
?
b. +0.75 rad
c. ? degrees
d. + 135°
Angular speed describes rate of rotation
Linear speed describes the distance traveled in a specified interval of time.
Angular speed is similarly defined. The average angular speed, wavg (w is the
Greek letter omega), of a rotating rigid object is the ratio of the angular displacement, ∆q, to the time interval, ∆t, that the object takes to undergo that displacement. Angular speed describes how quickly the rotation occurs.
angular speed
the rate at which a body rotates
about an axis, usually expressed
in radians per second
ANGULAR SPEED
∆q

wavg = 
∆t
angular displacement
average angular speed = 
time interval
Angular speed is given in units of radians per second (rad/s). Sometimes
angular speeds are given in revolutions per unit time. Recall that 1 rev = 2p rad.
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Rotational Motion and the Law of Gravity
247
Back
SAMPLE PROBLEM 7B
Angular speed
PROBLEM
A child at an ice cream parlor spins on a stool. The child turns counterclockwise with an average angular speed of 4.0 rad/s. In what time interval will the child’s feet have an angular displacement of 8.0p rad?
SOLUTION
Given:
∆q = 8.0p rad
Unknown:
∆t = ?
w avg = 4.0 rad/s
Use the angular speed equation from page 247. Rearrange to solve for ∆t.
∆q
w avg = 
∆t
∆q
∆t = 
wavg
8.0p rad
∆t =  = 2.0p s
4.0 rad/s
∆t = 6.3 s
PRACTICE 7B
Angular speed
1. A car tire rotates with an average angular speed of 29 rad/s. In what time
interval will the tire rotate 3.5 times?
2. A girl ties a toy airplane to the end of a string and swings it around her
head. The plane’s average angular speed is 2.2 rad/s. In what time interval
will the plane move through an angular displacement of 3.3 rad?
3. The average angular speed of a fly moving in a circle is 7.0 rad/s. How
long does the fly take to move through 2.3 rad?
4. Fill in the unknown quantities in the following table:
wavg
?
a.
b. +0.75 rev/s
?
c.
d. +2p rad/s
248
Chapter 7
∆q
∆t
+2.3 rad
?
− 1.2 turns
+ 1.5p rad
1 0.0 s
0.050 s
1.2 s
?
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
t2
t1
(a)
(b)
Figure 7-5
w1
w2
An accelerating bicycle wheel
rotates with (a) an angular speed
w 1 at time t1 and (b) an angular
speed w 2 at time t2.
Angular acceleration occurs when angular speed changes
Figure 7-5 shows a bicycle turned upside down so that a repairperson can
work on the rear wheel. The bicycle pedals are turned so that at time t1 the
wheel has angular speed w1 , as shown in Figure 7-5(a), and at a later time, t2,
it has angular speed w2 , as shown in Figure 7-5(b).
The average angular acceleration, aavg (a is the Greek letter alpha), of an
object is given by the relationship shown below. Angular acceleration has the
units radians per second per second (rad/s2).
angular acceleration
the time rate of change of angular speed, expressed in radians
per second per second
ANGULAR ACCELERATION
w2 − w1 ∆w
 = 
aavg = 
t2 − t1
∆t
change in angular speed
average angular acceleration = 
time interval
SAMPLE PROBLEM 7C
Angular acceleration
PROBLEM
A car’s tire rotates at an initial angular speed of 21.5 rad/s. The driver accelerates, and after 3.5 s the tire’s angular speed is 28.0 rad/s. What is
the tire’s average angular acceleration during the 3.5 s time interval?
SOLUTION
Given:
w1 = 21.5 rad/s
Unknown:
aavg = ?
w2 = 28.0 rad/s
∆t = 3.5 s
Use the angular acceleration equation on this page.
w2 − w1 28.0 rad/s − 21.5 rad/s 6.5 rad/s
 =  = 
aavg = 
3.5 s
∆t
3.5 s
aavg = 1.9 rad/s2
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Rotational Motion and the Law of Gravity
249
Back
PRACTICE 7C
Angular acceleration
1. A figure skater begins spinning counterclockwise at an angular speed of
4.0p rad/s. During a 3.0 s interval, she slowly pulls her arms inward and
finally spins at 8.0p rad/s. What is her average angular acceleration during this time interval?
2. What angular acceleration is necessary to increase the angular speed of a
fan blade from 8.5 rad/s to 15.4 rad/s in 5.2 s?
3. Fill in the unknown quantities in the following table:
aavg
?
a.
b. +0.75 rad/s2
?
c.
∆w
∆t
+ 1 2 1.5 rad/s
?
−1 .2 turns/s
7.0 s
0.050 s
1 .2 s
All points on a rotating rigid object have the same angular
acceleration and angular speed
If a point on the rim of a bicycle wheel had an angular speed greater than a
point nearer the center, the shape of the wheel would be changing. Thus, for a
rotating object to remain rigid, as does a bicycle wheel or a Ferris wheel, every
portion of the object must have the same angular speed and the same angular
acceleration. This fact is precisely what makes angular speed and angular
acceleration so useful for describing rotational motion.
COMPARING ANGULAR AND LINEAR QUANTITIES
Table 7-1
Angular substitutes
for linear quantities
Linear
Angular
x
q
v
w
a
a
250
Chapter 7
Compare the equations we have found thus far for rotational motion with
those we found for linear motion in Chapter 2. For example, compare the following defining equation for average angular speed with the defining equation for average linear speed:
qf − qi ∆q
wavg =  = 
tf − ti ∆t
xf − xi ∆x
vavg =  = 
tf − ti ∆t
The equations are similar, with q replacing x and w replacing v. Take careful
note of such similarities as you study rotational motion because nearly every
linear quantity we have encountered thus far has a corresponding twin in
rotational motion, as shown in Table 7-1.
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
Use kinematic equations for constant angular acceleration
In light of the similarities between variables in linear motion and those in rotational motion, it should be no surprise that the kinematic equations of rotational motion are similar to the linear kinematic equations in Chapter 2. The
equations of rotational kinematics under constant angular acceleration, along
with the corresponding equations for linear motion under constant acceleration, are summarized in Table 7-2. Note that the following rotational motion
equations apply only for objects rotating about a fixed axis.
Table 7-2
Rotational and linear kinematic equations
Rotational motion with constant angular acceleration
Linear motion with constant
acceleration
w f = w i + a∆t
vf = vi + a∆t
2
∆x = vi ∆t + 2a(∆t)2
w f 2 = w i2 + 2a(∆q)
vf 2 = vi2 + 2a(∆x)
∆q = 2(w i + w f )∆t
∆x = 2(vi + vf )∆t
1
1
I
ERA
NT
PHYSICS
TU
1
IVE •
CT
∆q = w i ∆t + 2a(∆t)
1
TOR
Module 8
“Angular Kinematics”
provides an interactive lesson
with guided problem-solving
practice to teach you about different kinds of angular motion,
including the types described
here.
Note the correlation between the rotational equations involving the angular
variables q, w, and a and the equations of linear motion involving x, v, and a.
The quantity w in these equations represents the instantaneous angular
speed of the rotating object rather than the average angular speed.
SAMPLE PROBLEM 7D
Angular kinematics
PROBLEM
The wheel on an upside-down bicycle moves through 11.0 rad in 2.0 s. What
is the wheel’s angular acceleration if its initial angular speed is 2.0 rad/s?
SOLUTION
Given:
∆q = 11.0 rad
Unknown:
a =?
∆t = 2.0 s
w i = 2.00 rad/s
Use the second angular kinematic equation from Table 7-2 to solve for a.
1
∆q = w i ∆t + 2a(∆t)2
a = 2(∆q − w i ∆t)/(∆t)2
a = 2[11.0 rad − (2.00 rad/s)(2.0 s)]/(2.0 s)2
a = 3.5 rad/s2
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Rotational Motion and the Law of Gravity
251
Back
PRACTICE 7D
Angular kinematics
1. What is the angular acceleration of the upside-down bicycle wheel in
Sample Problem 7D if it rotates through 18.0 rad in 5.00 s?
2. A diver performing a double somersault spins at an angular speed of
4.0p rad/s precisely 0.50 s after leaving the platform. Assuming the diver
begins with zero initial angular speed and accelerates at a constant rate,
what is the diver’s angular acceleration during the double somersault?
3. A fish swimming behind an oil tanker gets caught in a whirlpool created
by the ship’s propellers. The fish has an angular speed of 1.0 rad/s. After
4.5 s, the fish’s angular speed is 14.5 rad/s. If the water in the whirlpool
accelerates at a constant rate, what is the angular acceleration?
4. A remote-controlled car’s wheel accelerates at 22.4 rad/s2. If the wheel
begins with an angular speed of 10.8 rad/s, what is the wheel’s angular
speed after exactly three full turns?
5. How long does the wheel in item 4 take to make the three turns?
Section Review
1. Convert the following angles in degrees to radians:
a.
b.
c.
d.
25°
35°
128°
270°
2. A mosquito lands on a phonograph record 5.0 cm from the record’s center. If the record turns clockwise so that the mosquito travels along an arc
length of 5.0 cm, what is the mosquito’s angular displacement?
3. A bicyclist rides along a circular track. If the bicyclist travels around
exactly half the track in 10.0 s, what is his average angular speed?
4. Physics in Action Find the angular acceleration of a spinning
amusement-park ride that initially travels at 0.50 rad/s then accelerates
to 0.60 rad/s during a 0.50 s time interval.
5. Physics in Action What is the instantaneous angular speed of a
spinning amusement-park ride that accelerates from 0.50 rad/s at a constant angular acceleration of 0.20 rad/s2 for 1.0 s?
252
Chapter 7
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
7-2
Tangential and centripetal
acceleration
RELATIONSHIPS BETWEEN ANGULAR
AND LINEAR QUANTITIES
7-2 SECTION OBJECTIVES
As described at the beginning of Section 7-1, the motion of a point on a rotating object is most easily described in terms of an angle from a fixed reference
line. In some cases, however, it is useful to understand how the angular speed
and angular acceleration of a rotating object relate to the linear speed and linear acceleration of a point on the object.
Imagine a golfer swinging a golf club. The most effective method for hitting a golf ball a long distance involves swinging the club in an approximate
circle around the body. If the club head undergoes a large angular acceleration, then the linear acceleration of the club head as it is swung will be large.
This large linear acceleration causes the club head to strike the ball at a high
speed and produce a significant force on the ball. This section will explore the
relationships between angular and linear quantities.
•
Find the tangential speed of a
point on a rigid rotating
object using the angular
speed and the radius.
•
Solve problems involving tangential acceleration.
•
Solve problems involving
centripetal acceleration.
Objects in circular motion have a tangential speed
Imagine an amusement-park carousel rotating about its center. Because a
carousel is a rigid object, any two horses attached to the carousel have the same
angular speed and angular acceleration regardless of their respective distances
from the axis of rotation. However, if the two horses are different distances
from the axis of rotation, they have different tangential speeds. The tangential
speed of any point rotating about an axis is also called the instantaneous linear
speed of that point. The tangential speed of a horse on the carousel is its speed
along a line drawn tangent to its circular path. (Recall that the tangent to a circle is the line that touches the circle at one and only one point.) The tangential
speeds of two horses at different distances from the center of a carousel are represented in Figure 7-6.
Note that the speed of the horse at point A is represented by a shorter arrow
than the one that represents the speed of the horse at point B; this reflects the
difference between the tangential speeds of the two horses. The horse on the
outside must travel the same angular displacement during the same amount of
time as the horse on the inside. To achieve this, the horse on the outside must
travel a greater distance, ∆s, than the horse on the inside. Thus, an object that is
farther from the axis of a rigid rotating body, such as a carousel or a Ferris
wheel, must travel at a higher tangential speed around the circular path, ∆s, to
travel the same angular displacement as would an object closer to the axis.
Copyright © by Holt, Rinehart and Winston. All rights reserved.
tangential speed
the instantaneous linear speed of
an object directed along the tangent to the object’s circular path
vt,outside
vt,inside
A
B
ω
Figure 7-6
Horses on a carousel move at the
same angular speed but different
tangential speeds.
Rotational Motion and the Law of Gravity
253
Back
NSTA
TOPIC: Rotational motion
GO TO: www.scilinks.org
sciLINKS CODE: HF2071
How can you find the tangential speed? Again consider the rotating carousel.
If the carousel rotates through an angle ∆q, a horse rotates through an arc
length ∆s in the interval ∆t. The angular displacement of the horse is given by
the equation for angular displacement.
∆s
∆q = 
r
To find the tangential speed of the horse, divide both sides of the equation
by the time the horse takes to travel the distance ∆s.
∆q 1 ∆s
 =  
∆t r ∆t
From Section 7-1, you know that the left side of the equation equals wavg.
Similarly, ∆s is a linear distance, so ∆s divided by ∆t is a linear speed along an
arc length. If ∆t is very short, then ∆s is so small that it is nearly tangent to the
circle; therefore, the speed is the tangential speed.
TANGENTIAL SPEED
vt = rw
tangential speed = distance from axis × angular speed
Note that w is the instantaneous angular speed, rather than the average angular speed, because the time interval is so short. This equation is valid only when w
is measured in radians per unit of time. Other measures of angular speed, such as
degrees per second and revolutions per second, must not be used in this equation.
SAMPLE PROBLEM 7E
Tangential speed
PROBLEM
The radius of a CD in a computer is 0.0600 m. If a microbe riding on the
disc’s rim has a tangential speed of 1.88 m/s, what is the disc’s angular speed?
SOLUTION
Given:
r = 0.0600 m
Unknown:
w =?
vt = 1.88 m/s
Use the tangential speed equation on this page to solve for angular speed.
vt = rw
v 1.88 m/s
w = t = 
r 0.0600 m
w = 31.3 rad/s
254
Chapter 7
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
PRACTICE 7E
Tangential speed
1. A woman passes through a revolving door with a tangential speed of
1.8 m/s. If she is 0.80 m from the center of the door, what is the door’s
angular speed?
2. A softball pitcher throws a ball with a tangential speed of 6.93 m/s. If the
pitcher’s arm is 0.660 m long, what is the angular speed of the ball before
the pitcher releases it?
3. An athlete spins in a circle before releasing a discus with a tangential
speed of 9.0 m/s. What is the angular speed of the spinning athlete?
Assume the discus is 0.75 m from the athlete’s axis of rotation.
4. Fill in the unknown quantities in the following table:
vt
?
a.
b. 0.75 m/s
?
c.
d. 2.0p m/s
w
r
1 2 1.5 rad/s
?
1 .2 turns/s
1 .5p rad/s
0.030 m
0.050 m
3.8 m
?
Tangential acceleration is tangent to the circular path
If a carousel speeds up, the horses on it experience an angular acceleration.
The linear acceleration related to this angular acceleration is tangent to the
circular path and is called the tangential acceleration.
Imagine that an object rotating about a fixed axis changes its angular speed
by ∆w in the interval ∆t. At the end of this time, the speed of a point on the
object has changed by the amount ∆vt . Using the equation for tangential
velocity on page 254 gives the following:
tangential acceleration
the instantaneous linear acceleration of an object directed along
the tangent to the object’s circular path
∆vt = r∆w
Dividing by ∆t gives
∆vt
∆w
 = r  
∆t
∆t
If the time interval ∆t is very small, then the left side of this relationship
gives the tangential acceleration of the point. The angular speed divided by
the time interval on the right side is the angular acceleration. Thus, the tangential acceleration of a point on a rotating object is given by the relationship
on the next page.
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Rotational Motion and the Law of Gravity
255
Back
TANGENTIAL ACCELERATION
at = ra
tangential acceleration = distance from axis × angular acceleration
Again, the angular acceleration in this equation refers to the instantaneous
angular acceleration. This equation must use the unit radians to be valid. In
SI, angular acceleration is expressed as radians per second per second.
SAMPLE PROBLEM 7F
Tangential acceleration
PROBLEM
A spinning ride at a carnival has an angular acceleration of 0.50 rad/s2. How
far from the center is a rider who has a tangential acceleration of 3.3 m/s2?
SOLUTION
Given:
a = 0.50 rad/s2
Unknown:
r=?
at = 3.3 m/s2
Use the tangential acceleration equation on this page. Rearrange to solve for r.
at = ra
a
3.3 m/s2
r = t = 2
a 0.50 rad/s
r = 6.6 m
PRACTICE 7F
Tangential acceleration
1. A dog on a merry-go-round undergoes a 1.5 m/s2 linear acceleration. If
the merry-go-round’s angular acceleration is 1.0 rad/s2, how far is the
dog from the axis of rotation?
2. A young boy swings a yo-yo horizontally above his head at an angular
acceleration of 0.35 rad/s2. If tangential acceleration of the yo-yo at the
end of the string is 0.18 m/s2, how long is the string?
3. What is a tire’s angular acceleration if the tangential acceleration at a
radius of 0.15 m is 9.4 × 10−2 m/s2?
256
Chapter 7
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
CENTRIPETAL ACCELERATION
Figure 7-7 shows a car moving in a circular path with a constant tangential speed of 30 km/h. Even though the car moves
at a constant speed, it still has an acceleration. To see why this
is, consider the defining equation for acceleration.
vf − vi

a=
tf − ti
Note that acceleration depends on a change in the velocity. Because velocity is a vector, there are two ways
an acceleration can be produced: by a change in the magnitude of the velocity and by a change in the direction of the
velocity. For a car moving in a circular path with constant
speed, the acceleration is due to a change in direction. An
acceleration of this nature is called a centripetal (centerseeking) acceleration. Its magnitude is given by the following equation:
Figure 7-7
Although the car moves at a constant speed of 30 km/h,
the car still has an acceleration because the direction of
the velocity changes.
v2
ac = t
r
centripetal acceleration
Consider Figure 7-8(a). An object is seen first at point A, with tangential
velocity vi at time ti , and then at point B, with tangential velocity vf at a later
time, tf . Assume that vi and vf differ in direction only and their magnitudes
are the same.
The change in velocity, ∆v = vf − vi, can be determined graphically, as
shown by the vector triangle in Figure 7-8(b). Note that when ∆t is very small
(as ∆t approaches zero), vf will be almost parallel to vi and the vector ∆v will
be approximately perpendicular to them, pointing toward the center of the
circle. This means that the acceleration will also be directed toward the center
of the circle because it is in the direction of ∆v.
Because the tangential speed is related to the angular speed through the
relationship vt = rw, the centripetal acceleration can be found using the angular speed as well.
acceleration directed toward the
center of a circular path
(a)
A vi
∆s
r
vf
∆θ
−vi
2
v
ac = t
r
ac = rw
r
∆θ
(b)
∆v
CENTRIPETAL ACCELERATION
B v
f
∆v = vf − vi = vf + (− vi )
2
Figure 7-8
2
(tangential speed)
centripetal acceleration = 
distance from axis
centripetal acceleration = distance from axis × (angular speed)2
Copyright © by Holt, Rinehart and Winston. All rights reserved.
(a) As the particle moves from A to
B, the direction of the particle’s
velocity vector changes. (b) Vector
addition is used to determine the
direction of the change in velocity,
∆v, which for short time intervals is
toward the center of the circle.
Rotational Motion and the Law of Gravity
257
Back
SAMPLE PROBLEM 7G
Centripetal acceleration
PROBLEM
A test car moves at a constant speed around a circular track. If the car is
48.2 m from the track’s center and has a centripetal acceleration of
8.05 m/s2, what is its tangential speed?
SOLUTION
Given:
r = 48.2 m
Unknown:
vt = ?
ac = 8.05 m/s2
Use the first centripetal acceleration equation from page 257. Rearrange to
solve for vt.
v2
ac = t
r
vt = acr = (8
.0
5m
/s
2)(4
8.
2m
)
vt = 19.7 m/s
PRACTICE 7G
Centripetal acceleration
1. A girl sits on a tire that is attached to an overhanging tree limb by a rope.
The girl’s father pushes her so that her centripetal acceleration is 3.0 m/s2.
If the length of the rope is 2.1 m, what is the girl’s tangential speed?
2. A young boy swings a yo-yo horizontally above his head so that the yo-yo
has a centripetal acceleration of 250 m/s2. If the yo-yo’s string is 0.50 m
long, what is the yo-yo’s tangential speed?
3. A dog sits 1.5 m from the center of a merry-go-round. If the dog undergoes a 1.5 m/s2 centripetal acceleration, what is the dog’s linear speed?
What is the angular speed of the merry-go-round?
4. A race car moves along a circular track at an angular speed of 0.512 rad/s.
If the car’s centripetal acceleration is 15.4 m/s2, what is the distance
between the car and the center of the track?
5. A piece of clay sits 0.20 m from the center of a potter’s wheel. If the potter spins the wheel at an angular speed of 20.5 rad/s, what is the magnitude of the centripetal acceleration of the piece of clay on the wheel?
258
Chapter 7
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
Tangential and centripetal accelerations are perpendicular
Centripetal and tangential acceleration are not the same. To understand why,
consider a car moving around a circular track. Because the car is moving in a
circular path, it always has a centripetal component of acceleration because its
direction of travel, and hence the direction of its velocity, is continually
changing. If the car’s speed is increasing or decreasing, the car also has a tangential component of acceleration. To summarize, the tangential component
of acceleration is due to changing speed; the centripetal component of acceleration is due to changing direction.
Find the total acceleration using the Pythagorean theorem
ac
When both components of acceleration exist simultaneously, the tangential
acceleration is tangent to the circular path and the centripetal acceleration
points toward the center of the circular path. Because these components of
acceleration are perpendicular to each other, the magnitude of the total acceleration can be found using the Pythagorean theorem, as follows:
at
2
atotal = at2+
a
c
Figure 7-9
The direction of the total acceleration, as shown in Figure 7-9, depends on
the magnitude of each component of acceleration and can be found using the
inverse of the tangent function.
θ
atotal
The direction of the total acceleration of a rotating object can be
found using the tangent function.
a
q = tan−1 c
at
Section Review
1. Find the tangential speed of a ball swung at a constant angular speed of
5.0 rad/s on a rope that is 5.0 m long.
2. If an object has a tangential acceleration of 10.0 m/s2, the angular speed
will do which of the following?
a. decrease
b. stay the same
c. increase
3. Physics in Action Find the tangential acceleration of a person
standing 9.5 m from the center of a spinning amusement-park ride that
has an angular acceleration of 0.15 rad/s2.
4. Physics in Action If a spinning amusement-park ride has an angular speed of 1.2 rad/s, what is the centripetal acceleration of a person
standing 12 m from the center of the ride?
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Rotational Motion and the Law of Gravity
259
Back
7-3
Causes of circular motion
7-3 SECTION OBJECTIVES
FORCE THAT MAINTAINS CIRCULAR MOTION
•
Calculate the force that
maintains circular motion.
•
Explain how the apparent
existence of an outward force
in circular motion can be
explained as inertia resisting
the force that maintains circular motion.
Consider a ball of mass m tied to a string of length r that is being whirled in a
horizontal circular path, as shown in Figure 7-10. Assume that the ball moves
with constant speed. Because the velocity vector, v, changes direction continuously during the motion, the ball experiences a centripetal acceleration
directed toward the center of motion, as described in Section 7-2, with magnitude given by the following equation:
•
Apply Newton’s universal law
of gravitation to find the
gravitational force between
two masses.
Fc
r
m
v
Figure 7-10
When a ball is whirled in a circle, a
force directed toward the center of
the ball’s circular path acts on it.
v2
ac = t
r
The inertia of the ball tends to maintain the ball’s motion in a straight-line
path; however, the string counteracts this tendency by exerting a force on the
ball that makes the ball follow a circular path. This force is directed along the
length of the string toward the center of the circle, as shown in Figure 7-10.
The magnitude of this force can be found by applying Newton’s second law
along the radial direction.
Fc = mac
The net force on an object directed toward the center of the object’s circular path is the force that maintains the object’s circular motion.
FORCE THAT MAINTAINS CIRCULAR MOTION
m vt2
Fc = 
r
Fc = mrw 2
NSTA
TOPIC: Circular motion
GO TO: www.scilinks.org
sciLINKS CODE: HF2072
(tangential speed)2
force that maintains circular motion = mass × 
distance to axis
force that maintains = mass × distance to axis × (angular speed)2
circular motion
The force that maintains circular motion is measured in the SI unit of
newtons. This force is no different from any of the other forces we have
studied. For example, friction between a race car’s tires and a circular racetrack provides the force that enables the car to travel in a circular path. As
another example, the gravitational force exerted on the moon by Earth provides the force necessary to keep the moon in its orbit.
260
Chapter 7
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
SAMPLE PROBLEM 7H
Force that maintains circular motion
PROBLEM
A pilot is flying a small plane at 30.0 m/s in a circular path with a radius of
100.0 m. If a force of 635 N is needed to maintain the pilot’s circular
motion, what is the pilot’s mass?
SOLUTION
Given:
vt = 30.0 m/s
Unknown:
m=?
r = 100.0 m
Fc = 635 N
Use the equation for force from page 260. Rearrange to solve for m.
v2
Fc = mt
r
r
100.0 m
m = Fc 2 = 635 N 2
vt
(30.0 m/s)
m = 70.6 kg
PRACTICE 7H
Force that maintains circular motion
1. A girl sits in a tire that is attached to an overhanging tree limb by a
rope 2.10 m in length. The girl’s father pushes her with a tangential speed
of 2.50 m/s. If the magnitude of the force that maintains her circular
motion is 88.0 N, what is the girl’s mass?
2. A bicyclist is riding at a tangential speed of 13.2 m/s around a circular
track with a radius of 40.0 m. If the magnitude of the force that maintains the bike’s circular motion is 377 N, what is the combined mass of
the bicycle and rider?
3. A dog sits 1.50 m from the center of a merry-go-round with an angular
speed of 1.20 rad/s. If the magnitude of the force that maintains the dog’s
circular motion is 40.0 N, what is the dog’s mass?
4. A 905 kg test car travels around a 3.25 km circular track. If the magnitude
of the force that maintains the car’s circular motion is 2140 N, what is the
car’s tangential speed?
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Rotational Motion and the Law of Gravity
261
Back
A force directed toward the center is necessary for circular motion
(a)
Because the force that maintains circular motion acts at right angles to the
motion, it causes a change in the direction of the velocity. If this force vanishes, the object does not continue to move in its circular path. Instead, it
moves along a straight-line path tangent to the circle. To see this point, consider a ball that is attached to a string and is being whirled in a vertical circle,
as shown in Figure 7-11. If the string breaks when the ball is at the position
shown in Figure 7-11(a), the force that maintains circular motion will vanish
and the ball will move vertically upward. The motion of the ball will be that of
a free-falling body. If the string breaks when the ball is at the top of its circular
path, as shown in Figure 7-11(b), the ball will fly off horizontally in a direction tangent to the path, then move in the parabolic path of a projectile.
(b)
Figure 7-11
A ball is whirled in a vertical circular path on the end of a string.
When the string breaks at the position shown in (a), the ball moves
vertically upward in free fall. (b)
When the string breaks at the top
of the ball’s path, the ball moves
along a parabolic path.
DESCRIBING THE MOTION OF
A ROTATING SYSTEM
To better understand the motion of a rotating system, consider a car
approaching a curved exit ramp to the left at high speed. As the driver makes
the sharp left turn, the passenger slides to the right and hits the door. At that
point, the force of the door keeps the passenger from being ejected from the
car. What causes the passenger to move toward the door? A popular explanation is that there must be a force that pushes the passenger outward. This force
is sometimes called the centrifugal force, but that term often creates confusion, so it is not used in this textbook.
Inertia is often misinterpreted as a force
1. Pizza
Pizza makers traditionally
form the crust by throwing
the dough up in the air and
spinning it. Why does this
make the pizza crust bigger?
2. Swings
The amusement-park ride
pictured below spins riders
around on swings attached
by cables from above. What
causes the swings to move
away from the center of the
ride when
the center
column begins to turn?
The phenomenon is correctly explained as follows: Before the car enters the
ramp, the passenger is moving in a straight-line path. As the car enters the
ramp and travels along a curved path, the passenger, because of inertia, tends
to move along the original straight-line path. This is in accordance with Newton’s first law, which states that the natural tendency of a body is to continue
moving in a straight line. However, if a sufficiently large force that maintains
circular motion (toward the center of curvature) acts on the passenger, the
person moves in a curved path, along with the car. The origin of the force that
maintains the circular motion of the passenger is the force of friction between
the passenger and the car seat. If this frictional force is not sufficient, the passenger slides across the seat as the car turns underneath. Because of inertia,
the passenger continues to move in a straight-line path. Eventually, the passenger encounters the door, which provides a large enough force to enable the
passenger to follow the same curved path as the car. The passenger slides
toward the door not because of some mysterious outward force but because
the force that maintains circular motion is not great enough to enable the passenger to travel along the circular path followed by the car.
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
NEWTON’S LAW OF UNIVERSAL GRAVITATION
Note that planets move in nearly circular orbits around the sun. As mentioned
earlier, the force that keeps these planets from coasting off in a straight line is
a gravitational force. The gravitational force is a field force that always exists
between two masses, regardless of the medium that separates them. It exists
not just between large masses like the sun, Earth, and moon but between any
two masses, regardless of size or composition. For instance, desks in a classroom have a mutual attraction because of gravitational force. The force
between the desks, however, is small relative to the force between the moon
and Earth because the gravitational force is proportional to the product of the
objects’ masses.
Gravitational force acts such that objects
are always attracted to one another. Examine the illustration of Earth and the moon
in Figure 7-12. Note that the gravitational
force between Earth and the moon is attractive, and recall that Newton’s third law
states that the force exerted on Earth by the
moon, FmE , is equal in magnitude to and in
the opposite direction of the force exerted
on the moon by Earth, FEm.
gravitational force
the mutual force of attraction
between particles of matter
FEm
FmE
Figure 7-12
The gravitational force between
Earth and the moon is attractive.
According to Newton’s third law,
FEm = FmE .
Gravitational force depends on the distance between two masses
If masses m1 and m2 are separated by distance r, the magnitude of the gravitational force is given by the following equation:
NEWTON’S LAW OF UNIVERSAL GRAVITATION
m m2
Fg = G 1
r2
NSTA
mass 1 × mass 2
gravitational force = constant × 2
(distance between center of masses)
TOPIC: Law of gravitation
GO TO: www.scilinks.org
sciLINKS CODE: HF2073
G is a universal constant called the constant of universal gravitation; it can
be used to calculate gravitational forces between any two particles and has
been determined experimentally.
N • m2
G = 6.673 × 10−11 
kg2
The law of universal gravitation is an example of an inverse-square law,
because the force varies as the inverse square of the separation. That is, the
force between two masses decreases as the masses move farther apart.
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Rotational Motion and the Law of Gravity
263
Back
Gravitational force is localized to the center of a spherical mass
The astronomer Johannes Kepler
proposed that planets orbit the sun
in elliptical paths. However, some scientists continued to believe that
Earth was the center of the solar
system until Sir Isaac Newton
showed that elliptical orbits could be
predicted using his laws of motion.
The gravitational force exerted by a spherical mass on a particle outside the
sphere is the same as it would be if the entire mass of the sphere were concentrated at its center. For example, the force on an object of mass m at Earth’s
surface has the following magnitude:
M m
Fg = G E
RE2
ME is Earth’s mass and RE is its radius. This force is directed toward the
center of Earth. Note that this force is in fact the weight of the mass, mg.
M m
mg = G E
RE2
By substituting the actual values for the mass and radius of Earth, we can
find the value for g and compare it with the value of free-fall acceleration used
throughout this book.
Because m occurs on both sides of the equation above, these masses cancel.
2
ME
5.98 × 1024 kg
−11 N • m



 = 9.83 m/s2
g = G 
=
6.673
×
10
RE2
kg2 (6.37 × 106 m)2
This value for g is approximately equal to the value used throughout this
book. The difference is due to rounding the values for Earth’s mass and radius.
SAMPLE PROBLEM 7 I
Gravitational force
PROBLEM
Find the distance between a 0.300 kg billiard ball and a 0.400 kg billiard ball
if the magnitude of the gravitational force is 8.92 1011 N.
SOLUTION
Given:
m1 = 0.300 kg
Unknown:
r=?
Fg = 8.92 × 10−11 N
m2 = 0.400 kg
Use the equation for Newton’s Law of Universal Gravitation.
2
−11N • m


6.673
×
10
2
G
kg (0.300 kg)(0.400 kg)
r 2 = m1m2 =
Fg
= 8.97 × 10−2 m2
2 2
r = 8.
0−
m
97
×1
= 3.00 × 10−1 m
264
Chapter 7
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
PRACTICE 7 I
Gravitational force
1. If the mass of each ball in Sample Problem 7I is 0.800 kg, at what distance between the balls will the gravitational force between the balls have
the same magnitude as that in Sample Problem 7I? How does the change
in mass affect the magnitude of the gravitational force?
2. Mars has a mass of about 6.4 × 1023 kg, and its moon Phobos has a mass
of about 9.6 × 1015 kg. If the magnitude of the gravitational force between
the two bodies is 4.6 × 1015 N, how far apart are Mars and Phobos?
3. Find the magnitude of the gravitational force a 67.5 kg person would
experience while standing on the surface of each of the following planets:
Planet
a. Earth
b. Mars
c. Pluto
m
r
5.98 × 1024 kg
6.34 × 1023 kg
5 × 1023 kg
6.37 × 106 m
3.43 × 106 m
4 × 105 m
Section Review
1. A roller coaster moves through a vertical loop at a constant speed and suspends its passengers upside down. In what direction is the force that causes
the coaster and its passengers to move in a circle? What provides this force?
2. Identify the force that maintains the circular motion of the following:
a. a bicyclist moving around a flat circular track
b. a bicycle moving around a flat circular track
c. a bobsled turning a corner on its track
3. A 90.0 kg person stands 1.00 m from a 60.0 kg person sitting on a bench
nearby. What is the magnitude of the gravitational force between them?
4. Physics in Action A 90.0 kg person rides a spinning amusementpark ride that has an angular speed of 1.15 rad/s. If the radius of the ride
is 11.5 m, what is the magnitude of the force that maintains the circular
motion of the person?
5. Physics in Action Calculate the mass that a planet with the same
radius as Earth would need in order to exert a gravitational force equal to the
force on the person in item 4.
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Rotational Motion and the Law of Gravity
265
Back
Projectiles and satellites
As explained in Chapter 3, when a ball is thrown parallel to the ground, the
motion of the ball has two components of motion: a horizontal velocity, which
remains unchanged, and a vertical acceleration, which equals free-fall acceleration. Given this analysis, it may seem confusing to think of the moon and other
satellites in orbit around Earth as projectiles. But in fact, satellites are projectiles. As shown in Figure 7-13, the larger the velocity parallel to Earth’s surface,
the farther the projectile moves before striking Earth. Note, however, that at
some large velocity, the projectile returns to its point of origin without moving
closer to Earth. In this case, the gravitational force between the projectile
and Earth is just great enough to keep the projectile from moving
along its inertial straight-line path. This is how satellites stay in orbit.
Escape speed
Figure 7-13
When the speed of
a projectile is large
enough, the projectile orbits Earth as
a satellite.
266
Chapter 7
When the speed of an object, such as a rocket, is greater than the
speed required to keep it in orbit, the object can escape the gravitational pull of Earth and soar off into space. The object soars off
into space when its initial speed moves it out of the range in which
the gravitational force is significant. Mathematically, the value of this
escape speed (vesc ) is given by the following equation:
vesc =
2MG

R
Earth’s radius, R, is about 6.37 × 106 m, and its mass is approximately
5.98 × 1024 kg. Thus, the escape speed of a projectile from Earth is 1.12 × 104 m/s.
(Note that this value does not depend on the mass of the projectile in question.)
As the mass of a planet or other body increases and its radius decreases, the
escape speed necessary for a projectile to escape the gravitational pull of that
body increases, as shown in Figure 7-14. If the body has a very large mass and
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
a small radius, the speed necessary for a projectile to escape the gravitational
pull of that body reaches very high values. For example, an object with a mass
three times that of the sun but with a diameter of about 10 km would require
an escape speed equal to the speed of light. In other words, the force of gravity
such an object exerts on a projectile is so great that even light does not move
fast enough to escape it.
r2
r1
(a)
Figure 7-14
RS
(b)
(c)
Black holes
The existence of such massive objects was first predicted in 1916 by Karl
Schwarzschild, who used his solutions to Einstein’s general-relativity
equations to predict their properties. Thus, the distance from the center of
the object to the circular orbit at which escape speed is equal to the speed of
light is called the Schwarzschild radius. Because light cannot escape from any
point within the sphere defined by the Schwarzschild radius, no information
can be obtained about events that occur in this region. Hence, the edge of the
sphere is called the event horizon, and the apparently lightless region within it
is called a black hole.
Recent observations have provided strong
evidence for the existence of black holes.
Tremendous amounts of X rays and other
radiation have been observed coming from
regions that are near visible stars, although
no stars appear to be the source of the radiation. If the visible star has a black hole as a
companion, it could be losing some of its
outer atmosphere to the black hole, and those
atmospheric gases could be emitting radiation
as they accelerate closer to the black hole.
Candidates for black holes of these types
include Scorpius X-1 and Cygnus X-1.
The large amount of energy that galactic centers produce suggests to
many astrophysicists that the energy sources are supermassive black holes.
The galaxy NGC 4261, shown in Figure 7-15, is likely to have a black hole at
its center. Some astronomers believe the Milky Way, our own galaxy, contains
a black hole about the size of our solar system.
Copyright © by Holt, Rinehart and Winston. All rights reserved.
NSTA
TOPIC: Black holes
GO TO: www.scilinks.org
sciLINKS CODE: HF2074
(a) A projectile that passes
near any massive object will be
bent from its trajectory. (b) The
more compact the object, the
nearer the projectile can
approach and the greater the
escape speed it needs. (c) If the
object is so small and massive
that a projectile’s escape speed
at distance RS is greater than the
speed of light, then the object is
classified as a black hole.
Figure 7-15
The gas jets and the central disk
shown at right, created by
combining an optical image with
a radio telescope image of NGC
426 1 , show signs of a black hole
in this galaxy’s center.
Rotational Motion and the Law of Gravity
267
Back
CHAPTER 7
Summary
KEY TERMS
KEY IDEAS
angular acceleration (p. 249)
Section 7-1 Measuring rotational motion
• The average angular speed, wavg , of a rigid, rotating object is defined as
the ratio of the angular displacement, ∆q, to the time interval, ∆t.
• The average angular acceleration, aavg , of a rigid, rotating object is defined
as the ratio of the change in angular speed, ∆w, to the time interval, ∆t.
angular displacement
(p. 246)
angular speed (p. 247)
centripetal acceleration
(p. 257)
gravitational force (p. 263)
radian (p. 245)
rotational motion (p. 244)
tangential acceleration
(p. 255)
tangential speed (p. 253)
Section 7-2 Tangential and centripetal acceleration
• A point on an object rotating about a fixed axis has a tangential speed
related to the object’s angular speed. When the object’s angular acceleration changes, the tangential acceleration of a point on the object changes.
• Uniform circular motion occurs when an acceleration of constant magnitude
is perpendicular to the tangential velocity.
Section 7-3 Causes of circular motion
• Any object moving in a circular path must have a net force exerted on it
that is directed toward the center of the circular path.
• Every particle in the universe attracts every other particle with a force that
is directly proportional to the product of the particles’ masses and inversely proportional to the square of the distance between the particles.
Diagram symbols
Variable symbols
Rotational
motion
Quantities
Units
s
arc length
m
meters
∆q
angular displacement
rad
radians
w
angular speed
rad/s
Angle
marking
radians/second
2
a
angular acceleration
rad/s
radians/second2
vt
tangential speed
m/s
meters/second
2
at
tangential acceleration
m/s
meters/second2
ac
centripetal acceleration
m/s2
meters/second2
Fc
force that maintains
circular motion
N
newtons
Fg
gravitational force
N
newtons
2
G
268
Chapter 7
constant of universal gravitation
N•m

kg 2
newtons • meters2

kilograms2
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
CHAPTER 7
Review and Assess
RADIANS AND ANGULAR MOTION
EQUATIONS FOR ANGULAR MOTION
Review questions
Practice problems
1. How many degrees equal p radians? How many
revolutions equal p radians?
2. What units must be used for q, w, and a in the kinematic equations for rotational motion listed in
Table 7-2?
3. Distinguish between linear speed and angular speed.
4. When a wheel rotates about a fixed axis, do all
points on the wheel have the same angular speed?
Practice problems
5. A car on a Ferris wheel has an angular displacement
of 0.34 rad. If the car moves through an arc length
of 12 m, what is the radius of the Ferris wheel?
(See Sample Problem 7A.)
6. When a wheel is rotated through an angle of 35°, a
point on the circumference travels through an arc
length of 2.5 m. When the wheel is rotated through
angles of 35 rad and 35 rev, the same point travels
through arc lengths of 143 m and 9.0 × 102 m,
respectively. What is the radius of the wheel?
(See Sample Problem 7A.)
7. How long does it take the second hand of a clock to
move through 4.00 rad?
(See Sample Problem 7B.)
8. A phonograph record has an initial angular speed of
33 rev/min. The record slows to 11 rev/min in 2.0 s.
What is the record’s average angular acceleration
during this time interval?
(See Sample Problem 7C.)
9. If a flywheel increases its average angular speed by
2.7 rad/s in 1.9 s, what is its angular acceleration?
(See Sample Problem 7C.)
Copyright © by Holt, Rinehart and Winston. All rights reserved.
10. A potter’s wheel moves from rest to an angular speed
of 0.20 rev/s in 30.0 s. Assuming constant angular
acceleration, what is its angular acceleration in rad/s2 ?
(See Sample Problem 7D.)
11. A drill starts from rest. After 3.20 s of constant angular
acceleration, the drill turns at a rate of 2628 rad/s.
a. Find the drill’s angular acceleration.
b. Determine the angle through which the drill
rotates during this period.
(See Sample Problem 7D.)
12. A tire placed on a balancing machine in a service station starts from rest and turns through 4.7 revs in
1.2 s before reaching its final angular speed. Assuming that the angular acceleration of the wheel is constant, calculate the wheel’s angular acceleration.
(See Sample Problem 7D.)
TANGENTIAL AND CENTRIPETAL
ACCELERATION
Review questions
13. When a wheel rotates about a fixed axis, do all the
points on the wheel have the same tangential speed?
14. Correct the following statement: The racing car
rounds the turn at a constant velocity of 145 km/h.
15. Describe the path of a moving body whose acceleration is constant in magnitude at all times and is perpendicular to the velocity.
16. An object moves in a circular path with constant
speed v.
a. Is the object’s velocity constant? Explain.
b. Is its acceleration constant? Explain.
Rotational Motion and the Law of Gravity
269
Back
Conceptual questions
17. Give an example of a situation in which an automobile driver can have a centripetal acceleration but no
tangential acceleration.
18. Can a car move around a circular racetrack so that
the car has a tangential acceleration but no centripetal acceleration?
19. The gas pedal and the brakes of a car accelerate and
decelerate the car. Could a steering wheel perform
either of these two actions? Explain.
20. It has been suggested that rotating cylinders about
16 km long and 8 km in diameter should be placed
in space for future space colonies. The rotation
would simulate gravity for the inhabitants of these
colonies. Explain the concept behind this proposal.
26. A sock stuck to the side of a clothes-dryer barrel has
a centripetal acceleration of 28 m/s2. If the dryer
barrel has a radius of 27 cm, what is the tangential
speed of the sock?
(See Sample Problem 7G.)
CAUSES OF CIRCULAR MOTION
Review questions
27. Imagine that you attach a heavy object to one end of a
spring and then, while holding the spring’s other end,
whirl the spring and object in a horizontal circle. Does
the spring stretch? Why? Discuss your answer in
terms of the force that maintains circular motion.
28. Why does the water remain in a pail that is whirled
in a vertical path, as shown in Figure 7-16?
Practice problems
21. A small pebble breaks loose from the treads of a tire
with a radius of 32 cm. If the pebble’s tangential
speed is 49 m/s, what is the tire’s angular speed?
(See Sample Problem 7E.)
22. The Emerald Suite is a revolving restaurant at the
top of the Space Needle in Seattle, Washington. If a
customer sitting 12 m from the restaurant’s center
has a tangential speed of 2.18 × 10−2 m/s, what is
the angular speed of the restaurant?
(See Sample Problem 7E.)
23. A bicycle wheel has an angular acceleration of
1.5 rad/s2. If a point on its rim has a tangential acceleration of 48 cm/s2, what is the radius of the wheel?
(See Sample Problem 7F.)
Figure 7-16
29. Identify the influence of mass and distance on
gravitational forces.
30. Explain the difference between centripetal acceleration and angular acceleration.
31. Comment on the statement, “There is no gravity in
outer space.”
24. When the string is pulled in the correct direction on a
window shade, a lever is released and the shaft that the
shade is wound around spins. If the shaft’s angular
acceleration is 3.8 rad/s2 and the shade accelerates
upward at 0.086 m/s2, what is the radius of the shaft?
(See Sample Problem 7F.)
Conceptual questions
25. A building superintendent twirls a set of keys in a
circle at the end of a cord. If the keys have a centripetal acceleration of 145 m/s2 and the cord has a
length of 0.34 m, what is the tangential speed of the
keys?
(See Sample Problem 7G.)
34. Why does mud fly off a rapidly turning wheel?
270
Chapter 7
32. Explain why Earth is not spherical in shape and why
it bulges at the equator.
33. Because of Earth’s rotation, you would weigh slightly
less at the equator than you would at the poles. Why?
35. Astronauts floating around inside the space shuttle
are not actually in a zero-gravity environment. What
is the real reason astronauts seem weightless?
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
36. A girl at a state fair swings a ball in a vertical circle at
the end of a string. Is the force applied by the string
greater than the weight of the ball at the bottom of
the ball’s path?
MIXED REVIEW PROBLEMS
Practice problems
42. The tub within a washer goes into its spin cycle, starting from rest and reaching an angular speed of
11p rad/s in 8.0 s. At this point, the lid is opened, and
a safety switch turns off the washer. The tub slows to
rest in 12.0 s. Through how many revolutions does
the tub turn? Assume constant angular acceleration
while the machine is starting and stopping.
37. A roller-coaster car speeds down a hill past point A
and then rolls up a hill past point B, as shown in
Figure 7-17.
a. The car has a speed of 20.0 m/s at point A. If the
track exerts a force on the car of 2.06 × 104 N at
this point, what is the mass of the car?
b. What is the maximum speed the car can have
at point B for the gravitational force to hold it
on the track?
(See Sample Problem 7H.)
B
10.0 m
15.0 m
A
Figure 7-17
38. Tarzan tries to cross a river by swinging from one
bank to the other on a vine that is 10.0 m long. His
speed at the bottom of the swing, just as he clears
the surface of the river, is 8.0 m/s. Tarzan does not
know that the vine has a breaking strength of 1.0 ×
103 N. What is the largest mass Tarzan can have and
make it safely across the river?
(See Sample Problem 7H.)
39. The gravitational force of attraction between two
students sitting at their desks in physics class is
3.20 × 10−8 N. If one student has a mass of 50.0 kg
and the other has a mass of 60.0 kg, how far apart
are the students sitting?
(See Sample Problem 7I.)
40. If the gravitational force between the electron (9.11 ×
10−31 kg) and the proton (1.67 × 10−27 kg) in a
hydrogen atom is 1.0 × 10−47 N, how far apart are the
two particles?
(See Sample Problem 7I.)
Copyright © by Holt, Rinehart and Winston. All rights reserved.
41. Find the average angular speed of Earth about the
sun in radians per second.
(Hint: Earth orbits the sun once every 365.25 days.)
43. An airplane is flying in a horizontal circle at a speed
of 105 m/s. The 80.0 kg pilot does not want the centripetal acceleration to exceed 7.00 times free-fall
acceleration.
a. Find the minimum radius of the plane’s path.
b. At this radius, what is the net force that maintains circular motion exerted on the pilot by
the seat belts, the friction against the seat, and
so forth?
44. A car traveling at 30.0 m/s undergoes a constant
negative acceleration of magnitude 2.00 m/s2 when
the brakes are applied. How many revolutions does
each tire make before the car comes to a stop,
assuming that the car does not skid and that the
tires have radii of 0.300 m?
45. A coin with a diameter of 2.40 cm is dropped onto a
horizontal surface. The coin starts out with an initial
angular speed of 18.0 rad/s and rolls in a straight line
without slipping. If the rotation slows with an angular acceleration of magnitude 1.90 rad/s2, how far
does the coin roll before coming to rest?
46. A mass attached to a 50.0 cm string starts from rest
and is rotated in a circular path exactly 40 times in
1.00 min before reaching a final angular speed. What
is the angular speed of the mass after 1.00 min?
47. A 13 500 N car traveling at 50.0 km/h rounds a
curve of radius 2.00 × 102 m. Find the following:
a. the centripetal acceleration of the car
b. the force that maintains centripetal acceleration
c. the minimum coefficient of static friction
between the tires and the road that will allow
the car to round the curve safely
Rotational Motion and the Law of Gravity
271
Back
48. A 2.00 × 103 kg car rounds a circular turn of radius
20.0 m. If the road is flat and the coefficient of static
friction between the tires and the road is 0.70, how
fast can the car go without skidding?
50. Find the centripetal accelerations of the following:
a. a point on the equator of Earth
b. a point at the North Pole of Earth
(See the table in the appendix for data on Earth.)
49. During a solar eclipse, the moon, Earth, and sun lie
on the same line, with the moon between Earth and
the sun. What force is exerted on
a. the moon by the sun?
b. the moon by Earth?
c. Earth by the sun?
(See the table in the appendix for data on the sun,
moon, and Earth.)
51. A copper block rests 30.0 cm from the center of a
steel turntable. The coefficient of static friction
between the block and the surface is 0.53. The
turntable starts from rest and rotates with a constant
angular acceleration of 0.50 rad/s2. After what time
interval will the block start to slip on the turntable?
(Hint: The normal force in this case equals the weight
of the block.)
Graphing calculators
Refer to Appendix B for instructions on downloading programs for your calculator. The program
“Chap7” allows you to analyze a graph of angular
speed versus time interval.
Angular speed, as you learned earlier in this
chapter, is described by the following equation:
∆q
wavg = 
∆t
The program “Chap7” stored on your graphing calculator makes use of the equation for angular speed.
Once the “Chap7” program is executed, your calculator will ask for the angular displacement in revolutions. The graphing calculator will use the
following equation to create a graph of the angular
speed (Y1) versus the time interval (X). Note that
the relationships in this equation are similar to
those in the angular speed equation shown above.
Y1 = (2p q)/X
a. Why is there a factor of 2p in the equation
used by your graphing calculator?
272
Chapter 7
First be certain your graphing calculator is in
radian mode by pressing m ∂ ∂ e.
Execute “Chap7” on the p menu and press
e to begin the program. Enter the value for the
angular displacement (shown below) and press e.
The calculator will provide a graph of the angular speed versus the time interval. (If the graph is
not visible, press w and change the settings for
the graph window, then press g.)
Press ◊ and use the arrow keys to trace along
the curve. The x-value corresponds to the time
interval in seconds, and the y-value corresponds to
the angular speed in radians per second.
Determine the angular speed in the following
situations:
b. a bowl on a mixer stand that turns 2.0 rev in 3.0 s
c. the same bowl on a mixer stand that has
slowed down to 2.0 rev in 4.0 s
d. a bicycle wheel turning 2.5 rev in 0.75 s
e. the same bicycle wheel turning 2.5 rev in 0.35 s
f. The x- and y-axes are said to be asymptotic to
the curve of angular speed versus time interval.
What does this mean?
Press @ q to stop graphing. Press e to
input a new value or ı to end the program.
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
52. An air puck of mass 0.025 kg is tied to a string and
allowed to revolve in a circle of radius 1.0 m on a
frictionless horizontal surface. The other end of the
string passes through a hole in the center of the surface, and a mass of 1.0 kg is tied to it, as shown in
Figure 7-19. The suspended mass remains in equilibrium while the puck revolves on the surface.
a. What is the magnitude of the force that maintains circular motion acting on the puck?
b. What is the linear speed of the puck?
53. In a popular amusement-park ride, a cylinder of
radius 3.00 m is set in rotation at an angular speed of
5.00 rad/s, as shown in Figure 7-20. The floor then
drops away, leaving the riders suspended against the
wall in a vertical position. What minimum coefficient
of friction between a rider’s clothing and the wall of
the cylinder is needed to keep the rider from slipping?
(Hint: Recall that Fs = ms Fn , where the normal force
is the force that maintains circular motion.)
Figure 7-20
Figure 7-19
Alternative Assessment
Performance assessment
1. Turn a bicycle upside down. Make two marks on
one spoke on the front wheel, one mark close to the
rim and another mark closer to the axle. Then spin
the front wheel. Which point seems to be moving
fastest? Have partners count the rotations of one
mark for 10 s or 20 s. Find the angular speed and
the linear speed of each point. Reassign the
observers to different points, and repeat the experiment. Make graphs to analyze the relationship
between the linear and angular speeds.
2. When you ride a bicycle, the rotational motion you
create on the pedals is transmitted to the back wheel
through the primary sprocket wheel, the chain, and
the secondary sprocket wheel. Study the connection
between these components and measure how the
angular and linear speeds change from one part of
the bicycle to another. How does the velocity of the
Copyright © by Holt, Rinehart and Winston. All rights reserved.
back wheel compare with that of the pedals on a
bicycle? Demonstrate your findings in class.
Portfolio projects
3. Research the historical development of the concept
of gravitational force. Find out how scientists’ ideas
about gravity have changed over time. Identify the
contributions of different scientists, such as Galileo,
Kepler, Newton, and Einstein. How did each scientist’s work build on the work of earlier scientists?
Analyze, review, and critique the different scientific
explanations of gravity. Focus on each scientist’s
hypotheses and theories. What are their strengths?
What are their weaknesses? What do scientists think
about gravity now? Use scientific evidence and
other information to support your answers. Write a
report or prepare an oral presentation to share your
conclusions.
Rotational Motion and the Law of Gravity
273
Back
CHAPTER 7
Laboratory Exercise
OBJECTIVES
•Examine the relationship
between the force that
maintains circular
motion, the radius, and
the tangential speed of a
whirling object.
CIRCULAR MOTION
In this experiment, you will construct a device for measuring the tangential
speed of an object undergoing circular motion, and you will determine how
the force and the radius affect the tangential speed of the object.
SAFETY
MATERIALS LIST
✔ 1.5 m nylon cord
✔ 2-hole rubber stopper
✔ masking tape
✔ meterstick
✔ PVC tube, about 15 cm long
and 1 cm in diameter
✔ set of masses
✔ stopwatch
• Tie back long hair, secure loose clothing, and remove loose jewelry to
prevent their getting caught in moving or rotating parts.
• Wear eye protection and perform this experiment in a clear area.
Swinging or dropped masses can cause serious injury.
PREPARATION
1. Read the entire lab, and plan what measurements you will take.
2. Prepare a data table in your lab notebook with five columns and fifteen
rows. In the first row, label the columns Trial, Hanging mass (kg), Mass of
stopper (kg), Total time (s), Radius (m). In the first column, label the second through fifteenth rows 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, and 14.
PROCEDURE
Constant radius with varying force
3. Measure the mass of the rubber stopper, and record it in your data table.
Fasten one end of the nylon cord securely to the rubber stopper. Pass the
other end of the cord through the PVC tube and securely fasten a 100 g mass
to the other end, as shown in Figure 7-21. Leave approximately 0.75 m of
cord between the top of the tube and the rubber stopper. Attach a piece of
masking tape to the cord just below the bottom of the tube.
4. Make sure the area is clear of obstacles, and warn other students that you
are beginning your experiment. Support the 100 g mass with one hand and
hold the PVC tube in the other. Make the stopper at the end of the cord circle around the top of the tube by moving the tube in a circular motion.
5. Slowly release the 100 g mass, and adjust the speed of the stopper so that
the masking tape stays just below the bottom of the tube. Make several
practice runs before recording any data.
274
Chapter 7
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Back
6. When you can keep the velocity of the stopper and the position of the
masking tape relatively constant, measure the time required for 20 revolutions of the stopper. Record the time interval in your data table in the
row labeled Trial 1. Repeat this trial and record the time interval in your
data table as Trial 2.
7. Place the apparatus on the lab table. Extend the cord so that it is taut and
the masking tape is in the same position it was in during the experiment.
Measure the length of the cord to the nearest millimeter from the center
of the top of the PVC tube to the center of the rubber stopper. Record this
distance in the data table as Radius for Trials 1 and 2.
8. Repeat the procedure using three different masses for Trials 3–8. Keep the
radius the same as in the first trial and use the same rubber stopper, but
increase the mass at the end of the cord each time. Do not exceed 500 g.
Attach all masses securely. Perform each trial two times, and record all
data in your data table.
Constant force with varying radius
9. For Trials 9–14, use the same stopper and the 100 g mass, and try three
different values for the radius in the range 0.50 m to 1.00 m. Make sure
that you have a clear area of at least 2.5 m in diameter to work in. Record
all data in your data table.
Figure 7-21
Step 3: To attach masses, make a
loop in the cord, place the mass
inside the loop, and secure the mass
with masking tape.
Step 4: You will need a clear area
larger than two times the radius.
Step 5: Spin the stopper so that
the cord makes a 90° angle with the
PVC tube. Release the mass slowly
without changing the speed.
Step 7: Make sure the cord is
held straight when you make your
measurements.
10. Clean up your work area. Put equipment away safely so that it is ready to
be used again.
ANALYSIS AND INTERPRETATION
Calculations and data analysis
1. Organizing data Calculate the weight of the hanging mass for each
trial. This weight is the force that maintains circular motion, Fc.
2. Organizing data For each trial, find the time necessary for one revolution of the stopper by dividing the total time required for 20 revolutions
by 20.
3. Organizing data Find the tangential speed for each trial.
2p r
a. Use the equation vt = .
∆t
Fc r
, where r is the radius of revolution and
m
m is the mass of the stopper.
b. Use the equation vt =
4. Graphing data Plot the following graphs:
a. Graph force versus tangential speed for Trials 1–8.
b. Graph tangential speed versus radius for Trials 9–14.
Copyright © by Holt, Rinehart and Winston. All rights reserved.
Rotational Motion and the Law of Gravity
275