* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Lecture6
Survey
Document related concepts
Radio transmitter design wikipedia , lookup
Index of electronics articles wikipedia , lookup
Flexible electronics wikipedia , lookup
Integrated circuit wikipedia , lookup
Audio power wikipedia , lookup
Operational amplifier wikipedia , lookup
Valve audio amplifier technical specification wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Surge protector wikipedia , lookup
Opto-isolator wikipedia , lookup
Power electronics wikipedia , lookup
Power MOSFET wikipedia , lookup
Current source wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Current mirror wikipedia , lookup
Rectiverter wikipedia , lookup
Transcript
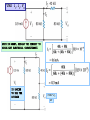
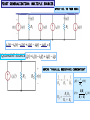
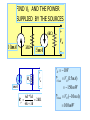
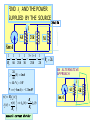
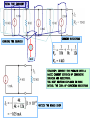
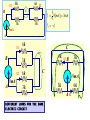
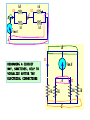
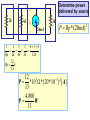
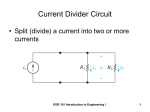
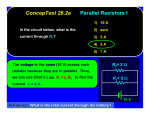
RESISTIVE CIRCUITS •SINGLE NODE-PAIR CIRCUIT ANALYSIS SINGLE NODE-PAIR CIRCUITS THESE CIRCUITS ARE CHARACTERIZED BY ALL THE ELMENTS HAVING THE SAME VOLTAGE ACROSS THEM - THEY ARE IN PARALLEL IN PRACTICE NODES MAY ASSUME STRANGE FORMS V EXAMPLE OF SINGLE NODE-PAIR V THIS ELEMENT IS INACTVE (SHORT-CIRCUITED) LOW DISTORTION POWER AMPLIFIER LOW VOLTAGE POWER SUPPLY FOR CRT - PARTIAL VIEW SAMPLE PHYSICAL NODES COMPONENT SIDE CONNECTION SIDE BASIC CURRENT DIVIDER Rp THE CURRENT DIVISION APPLY KCL THE CURRENT i(t) ENTERS THE NODE AND SPLITS - IT IS DIVIDED BETWEEN THE CURRENTS i1(t) AND i2(t) USE OHM’S LAW TO REPLACE CURRENTS DEFINE “PARALLEL RESISTANCE COMBINATION” i (t ) 1 v (t ) Rp v (t ) R1 R2 i (t ) R1 R2 I1 1 4 (5) 1mA I 2 I I1 (5) 1 4 1 4 FIND I1 , I2 , VO WHEN IN DOUBT… REDRAW THE CIRCUIT TO HIGHLIGHT ELECTRICAL CONNECTIONS!! IS EASIER TO SEE THE DIVIDER 80k * I 2 24V CAR STEREO AND CIRCUIT MODEL 215mA 215mA POWER PER SPEAKER LEARNING EXTENSION - CURRENT DIVIDER I1 120 (16) I1 12mA 120 40 THERE IS MORE THAN ONE OPTION TO COMPUTE I2 USING CURRENT DIVIDER KCL : I 2 16 I1 0 40 I2 (16) 4mA 120 40 POWER : I 2 R RESISTANCE IN k, P 144 * 40K 5.76W CURRENT IN mA YIELD POWER IN mW FIRST GENERALIZATION: MULTIPLE SOURCES APPLY KCL TO THIS NODE EQUIVALENT SOURCE DEFINE “PARALLEL RESISTANCE COMBINATION” iO ( t ) 1 v (t ) Rp v (t ) R1 R2 iO ( t ) R1 R2 FIND VO AND THE POWER SUPPLIED BY THE SOURCES 6k 10mA 3k Rp 5mA VO 15mA VO 10V VO P15mA VO (15mA) 6k * 3k Rp 2 k 6k 3k 150mW P10mA VO (10mA) 100mW SECOND GENERALIZATION: MULTIPLE RESISTORS APPLY KCL TO THIS NODE Ohm’s Law at every resistor v ( t ) RP i O ( t ) R v (t ) i K (t ) p iO (t ) ik (t ) Rk Rk General current divider FIND i1 AND THE POWER SUPPLIED BY THE SOURCE 20k||5k i1 4k 20k 5k 8mA 1 1 1 1 5 1 4 1 Rp 2k R p 4k 20k 5k 20k 2k 2k i1 (8) 4mA 4k v 4k * i1 16V AN ALTERNATIVE APPROACH i1 P v (8mA ) 128mW v ( t ) RP i O ( t ) R v (t ) i K (t ) p iO (t ) ik (t ) Rk Rk General current divider 4k 8mA 4k FIND THE CURRENT IL COMBINE RESISTORS COMBINE THE SOURCES 1mA STRATEGY: CONVERT THE PROBLEM INTO A BASIC CURRENT DIVIDER BY COMBINING SOURCES AND RESISTORS. THE NEXT SECTION EXPLORES IN MORE DETAIL THE IDEA OF COMBINING RESISTORS NOTICE THE MINUS SIGN I1 6k 6k I2 C B 3 I1 9[mA] 3mA 9 I 2 I1 3k 3k 9mA A I1 B 6k C 6k 3k I2 6k B C 9mA A I1 3k 9mA 3k 6k A I2 DIFFERENT LOOKS FOR THE SAME ELECTRIC CIRCUIT 3k I1 6k I2 6k C B 3k 3k 9mA A B REDRAWING A CIRCUIT MAY, SOMETIMES, HELP TO VISUALIZE BETTER THE ELECTRICAL CONNECTIONS I1 9mA A 6k I2 6k 3k C 3k Determine power delivered by source + 2k 4k V _ 3k 20mA P Rp * (20mA) 1 1 1 1 63 4 Rp 2k 4k 3k 12k 12 Rp k 13 12 P *103 * (20 *103 ) 2 [ A] 13 4.800 P W 13 2