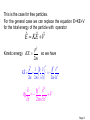Download Document

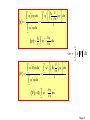
Quantum Mechanics
Lecture-6
Reference: Concept of Modern Physics
by “A. Beiser”
Page 1
Expectation Values
In the case of SE , wave function gives the information in
terms of probabilities and not specific numbers.
Therefore, instead of finding the average value of any term (for example
position of particle x ), we find the expectation value <x> of that.
Ni xi

Now,
x
 Ni
We must replace the number N i of particles atxi
that the particle be found in an interval dx xat
i
integration.

<x> 

x 
2
by the probability Pi
and summation by
dx




2
dx

Page 2
The denominator equals the probability that the particle
exists some where between x=  to x=  and therefore
it is equal to 1.
So expectation value for position is

<x> =
x
2
dx

The same procedure can be used to obtain expectation value
of any quantity :
Potential energy V(x) which is a function of x.
The expectation value for p can not be calculated this way.
According to uncertainty principle:
Page 3
If we specify x, so x  0 , we can not specify a
corresponding p since xp  / 2. The same problem occurs
for the expectation value of E.
OPERATORS:
A proper way to evaluate expectation values for p and E comes
from differentiating free particle wave function
(x , t) = A e-(2i/h)(Et-px)

2 i
i

p  p
x
h

2 i
i

E   E
t
h


i x

E  i

t
p 
Page 4


i x

E  i

t
p 
Looking at this we can say that quantity p corresponds to


i
differential operator
and E to
t . Thus the operator
i x
instructs us to take partial derivative of function that comes
after it.

 p̂
i x
So momentum operator :
And total energy operator:
i

ˆ
 E
t
Page 5
This is the case for free particles.
For the general case we can replace the equation E=KE+V
for the total energy of the particle with operator
Eˆ  KEˆ  Vˆ
p2
Kinetic energy KE 
so we have
2m
2
2
2
ˆ
p
1




KEˆ 
 
 
2m 2m  i x 
2m x 2
2


i

V
2
t
2m x
2
2
Page 6
Now we multiply the equation with

we get
2

 2
i

 V
2
t
2m x
which is the SWE.
Because p and E can be replaced by their corresponding
operators in an equation, we can use these to obtain their
expectation values.
Page 7

p 


 * p̂dx



 * dx
  
* 

  i x    dx

1


p 
i

* 


dx
x

<x> =

E 


 *Êdx


  dx
*
  
* 

i
  t    dx

1
x
2
dx



E i


* 

dx
t
Page 8
Let us see why expectation values involving operators have
to be expressed in the form

p 

ˆ dx
*p

The other alternatives are




*
*
ˆ  dx 
p  p
   dx  
 
0





i  x
i

*
since
*and  must be 0 at x=

p 

 and

ˆ dx 
 p
*


 
dx

i 
x
*
which makes no sense.
Page 9
EIGENVALUES and EIGNFUNCTIONS
Schrödinger's time independent wave equation
h 2 d 2
- 2
 V  E
2
8 m dx
d 2 82 m
 2 (E  V)  0
2
dx
h
This is the ‘steady state or ‘timeindependent’
form
of
Schrödinger
equation.
Note: Wave function
independent.-------- Ψ(x).
is
time
Page 10
The values of energy En for which, this steady state
equation can be solved are called eigen values and the
corresponding wave functions are called eigen functions.
Now
2
h 2 d 2
2
- 2
 V  E or E  V
2
2
8 m dx
2m x
So total energy operator can also be written as
2
Ĥ  V
2
2m x
2
Page 11
Therefore,
Hˆ n  En n
So we can say that the values En are the eigenvalues
of the Hamiltonian operator H. The function n
Is called eigen function.

So we can summarize the various operators used in Q.M
Page 12
Position
x  xˆ  x
Linear Momentum
px  pˆ x  i
Momentum in 3D
p  pˆ  i 
Total Energy
Kinetic Energy
Potentail Energy
Total Energy

x

ˆ
EEi
t
2
2
2
p̂

KEˆ 

2m
2m x 2
ˆ
V(x)  V(x)
 V(x)
2
p̂
ˆ [
HH
 V]
2m
(Hamiltonian form)
Page 13
Example:
function sin 2x
d2
operator   2
dx
eigenvalue  ?
Solution:
d2
 2 (sin 2x)  4(sin 2x)
dx
eigenvalue
Note: In Quantum mechanics, the allowed eigenfunction
1. must be finite for all x
2. must be single-valued for all x
3. must be continuous for all x
Page 14
Exercise: Determine < x > for a particle in a box of length ‘L’.
2
nx
 n (x) 
sin
L
L
L
 x    n (x) * x  n (x)dx
0
2
2 nx
  x sin
dx
L0
L
L
2
2L
L


L4
2
Exercise: Determine < p > for a particle in a box of length ‘L’.

2 n
nx
nx
 p    * (x)
 (x)dx 
sin
cos
dx

i x
i L L 0
L
L
0
L
L
L
2
1

k  sin(kx) cos(kx)dx  0 (sin ce  sin ax cos ax dx  sin 2 ax)
Li 0
2a
 2 nx 
2
2
 p  sin

0
(sin
0

sin
n  0, n  1, 2,3,....)

iL 
L 0
L
Page 15
Exercise: A Particle limited to the x-axis has the wave
function  =ax between x=0 and x=1; =0 elsewhere.
(a)Find the probability that the particle can be found x=0.45
and x=0.55.
(b)Find the expectation value < x > of the particle’s position.
(a) 0.0251 a2
(b) a2/4
Page 16
 Condition of normalized wavefunction
   d  1
*
1
   d  1
*
2
or
1
2
1 and  2 called normalized wavefunction.
 Condition for orthogonal wavefunction
*

 21d  0
or
   d  0
*
1
2
wavefunction 1 and  2 are mutually orthogonal
 Condition of orthonormal function
*

 i  jd  0
=1
if i  j
if
i=j
Page 18