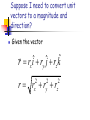Download Sample Problem

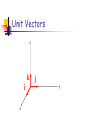
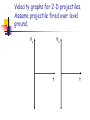
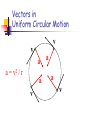
Lesson
Vectors Review
Scalars vs Vectors

Scalars have magnitude only


Distance, speed, time, mass
Vectors have both magnitude and direction

displacement, velocity, acceleration

tail
R
head
Direction of Vectors


The direction of a vector is
represented by the direction in which
the ray points.
This is typically given by an angle.
A

x
Magnitude of Vectors



A
The magnitude of a vector is the size of whatever the
vector represents.
The magnitude is represented by the length of the
vector.
Symbolically, the magnitude is often represented as
│A │
If vector A represents a
displacement of three miles to the
north…
Then vector B, which is twice as long,
would represent a displacement of six
miles to the north!
B
Equal Vectors

Equal vectors have
the same length and
direction, and
represent the same
quantity (such as
force or velocity).
Inverse Vectors

Inverse vectors have the same length, but
opposite direction.
A
-A
Graphical Addition of Vectors



Vectors are added graphically together head-totail.
The sum is called the resultant.
The inverse of the sum is called the equilibrant
B
A
R
A+B=R
Component Addition of Vectors
1)
Resolve each vector into its x- and ycomponents.
Ax = Acos
Bx = Bcos
2)
3)
4)
Ay = Asin
By = Bsin
etc.
Add the x-components together to get Rx
and the y-components to get Ry.
Use the Pythagorean Theorem to get the
magnitude of the resultant.
Use the inverse tangent function to get the
angle.
• Sample problem: Add together the following graphically
and by component, giving the magnitude and direction of
the resultant and the equilibrant.
– Vector A: 300 m @ 60o
– Vector B: 450 m @ 100o
– Vector C: 120 m @ -120o
Lesson
Unit Vectors
Consider Three Dimensions
Polar Angle
z
Azimuthal Angle
az
a

f
ay
y
ax
xy Projection
x
Unit Vectors

Unit vectors are quantities that specify
direction only. They have a magnitude of
exactly one, and typically point in the x, y, or z
directions.
iˆ points in the x direction
ˆj points in the y direction
kˆ points in the z direction
Unit Vectors
z
i
x
k j
y
Unit Vectors


Instead of using magnitudes and directions, vectors can
be represented by their components combined with their
unit vectors.
Example: displacement of 30 meters in the +x direction
added to a displacement of 60 meters in the –y direction
added to a displacement of 40 meters in the +z direction
yields a displacement of:
(30iˆ -60 ˆj  40kˆ) m
30,-60,40 m
Adding Vectors Using Unit
Vectors

Simply add all the i components
together, all the j components
together, and all the k components
together.
Sample problem: Consider two vectors, A = 3.00 i + 7.50 j and B
= -5.20 i + 2.40 j. Calculate C where C = A + B.
Sample problem: You move 10 meters north and 6 meters east.
You then climb a 3 meter platform, and move 1 meter west on
the platform. What is your displacement vector? (Assume
East is in the +x direction).
Suppose I need to convert unit
vectors to a magnitude and
direction?

Given the vector
ˆ
ˆ
ˆ
r  rx i  ry j  rz k
r  r r r
2
x
2
y
2
z
Sample problem: You move 10 meters north and 6 meters east.
You then climb a 3 meter platform, and move 1 meter west on
the platform. How far are you from your starting point?
Lesson
Position, Velocity, and
Acceleration Vectors in Multiple
Dimensions
1 Dimension




2 or 3 Dimensions
x: position
x: displacement
v: velocity
a: acceleration

In Unit Vector
Notation







r: position
r: displacement
v: velocity
a: acceleration
r=xi+yj+zk
r = x i + y j + z k
v = v x i + vy j + v z k
a = ax i + ay j + az k
Sample problem: The position of a particle is given by
r = (80 + 2t)i – 40j - 5t2k. Derive the velocity and acceleration
vectors for this particle. What does motion “look like”?
Sample problem: A position function has the form r = x i + y
j with x = t3 – 6 and y = 5t - 3.
a) Determine the velocity and acceleration functions.
b) Determine the velocity and speed at 2 seconds.
Miscellaneous



Let’s look at some video analysis.
Let’s look at a documentary.
Homework questions?
Lesson
Multi-Dimensional Motion with
Constant (or Uniform)
Acceleration
Sample Problem: A baseball outfielder throws a long ball. The
components of the position are x = (30 t) m and y = (10 t – 4.9t2) m
a) Write vector expressions for the ball’s position, velocity, and
acceleration as functions of time. Use unit vector notation!
b) Write vector expressions for the ball’s position, velocity, and
acceleration at 2.0 seconds.
Sample problem: A particle undergoing constant acceleration changes from
a velocity of 4i – 3j to a velocity of 5i + j in 4.0 seconds. What is the
acceleration of the particle during this time period? What is its
displacement during this time period?
Trajectory of Projectile
g
g
g


g
g
This shows the parabolic trajectory of a projectile
fired over level ground.
Acceleration points down at 9.8 m/s2 for the entire
trajectory.
Trajectory of Projectile
vx
vy
vx
vy
vx
vy
vx
vx

vy
The velocity can be resolved into components all
along its path. Horizontal velocity remains
constant; vertical velocity is accelerated.
Position graphs for 2-D projectiles.
Assume projectile fired over level
ground.
y
y
x
x
t
t
Velocity graphs for 2-D projectiles.
Assume projectile fired over level
ground.
Vy
Vx
t
t
Acceleration graphs for 2-D
projectiles. Assume projectile fired
over level ground.
ay
ax
t
t
Remember…
To work projectile problems…

…resolve the initial velocity into
components.
Vo

Vo,x = Vo cos 
Vo,y = Vo sin 
Sample problem: A soccer player kicks a ball at 15 m/s at an
angle of 35o above the horizontal over level ground. How far
horizontally will the ball travel until it strikes the ground?
Sample problem: A cannon is fired at a 15o angle above the
horizontal from the top of a 120 m high cliff. How long will it
take the cannonball to strike the plane below the cliff? How far
from the base of the cliff will it strike?
Lesson
Monkey Gun Experiment –
shooting on an angle
Lesson
A day of derivations
Sample problem: derive the trajectory equation.

 2
g
y  (tan  ) x   2
x
2 
 2vo cos  
Sample problem: Derive the range equation for a
projectile fired over level ground.
2v sin  cos
R
g
2
o
Sample problem: Show that maximum range is
obtained for a firing angle of 45o.
2v sin  cos
R
g
2
o
Will the projectile always hit the target presuming it has enough range? The
target will begin to fall as soon as the projectile leaves the gun.
Punt-Pass-Kick Pre-lab
• Purpose: Using only a stopwatch, a football field,
and a meter stick, determine the launch velocity
of sports projectiles that you punt, pass, or kick.
• Theory: Use horizontal (unaccelerated) motion
to determine Vx, and vertical (accelerated)
motion to determine Vy. Ignore air resistance.
• Data: Prepare your lab book to collect xi, xf, yo,
and t measurements for each sports projectile.
Analyze the data fully for at least three trials.
• Make sure you dress comfortably tomorrow!
Lesson
Punt-pass-kick lab
Lesson
Review of Uniform Circular
Motion
Radial and Tangential
Acceleration
Uniform Circular Motion



Occurs when an object moves in a circle without
changing speed.
Despite the constant speed, the object’s
velocity vector is continually changing;
therefore, the object must be accelerating.
The acceleration vector is pointed toward the
center of the circle in which the object is
moving, and is referred to as centripetal
acceleration.
Vectors in
Uniform Circular Motion
v
v
a
a = v2 / r
a
v
a
a
v
Sample Problem
The Moon revolves around the Earth every 27.3 days. The
radius of the orbit is 382,000,000 m. What is the
magnitude and direction of the acceleration of the Moon
relative to Earth?

Sample problem: Space Shuttle astronauts typically
experience accelerations of 1.4 g during takeoff. What
is the rotation rate, in rps, required to give an astronaut
a centripetal acceleration equal to this in a simulator
moving in a 10.0 m circle?
Tangential acceleration



Sometimes the speed of an object in circular motion is
not constant (in other words, it’s not uniform circular
motion).
An acceleration component may be tangent to the path,
aligned with the velocity. This is called tangential
acceleration. It causes speeding up or slowing down.
The centripetal acceleration component causes the
object to continue to turn as the tangential component
causes the speed to change. The centripetal component
is sometimes called the radial acceleration, since it lies
along the radius.
Tangential Acceleration
tangential component (aT )
v
If tangential
acceleration
exists, either
the speed or the
radius must
change. This is
no longer UCM.
a
radial or centripetal
component (ar or ac )
Sample Problem: Given the figure at right
v
rotating at constant radius, find the radial
and tangential acceleration components if  =
30o and a has a magnitude of 15.0 m/s2. What
is the speed of the particle at the location
shown? How is the particle’s speed changing?

5.00 m
a
Sample problem: Suppose you attach a ball to a 60 cm long
string and swing it in a vertical circle. The speed of the ball is
4.30 m/s at the highest point and 6.50 m/s at the lowest
point. Find the acceleration of the ball at the highest and
lowest points.
Sample problem: A car is rounding a curve on the interstate,
slowing from 30 m/s to 22 m/s in 7.0 seconds. The radius of the
curve is 30 meters. What is the acceleration of the car when its
speed is 22 m/s?
Lesson
Relative Motion
Derivation


Why is a = v2/r?
Follow along, and see a classic
derivation…
Relative Motion


When observers are moving at
constant velocity relative to each
other, we have a case of relative
motion.
The moving observers can agree
about some things, but not about
everything, regarding an object
they are both observing.
Consider two observers and a particle.
Suppose observer B is moving relative to
observer A.
P
particle
A
observer
B
observer
vrel
Also suppose particle P is also
moving relative to observer A.
P
vA
particle
In this case, it looks to A like P is moving to the right
at twice the speed that B is moving in the same
direction.
A
observer
B
observer
vrel
However, from the perspective
of observer B…
P
vB vA
particle
it looks like P is moving to the right at the same
speed that A is moving in the opposite direction, and
this speed is half of what A reports for P.
-vrel
A
observer
B
observer
vrel
The velocity measured by two
observers depends upon the observers’
velocity relative to each other.
P
vB vA
particle
-vrel
A
vB = vA – vrel
vA = vB + vrel
observer
B
observer
vrel
Sample problem: Now show that although velocity of the
observers is different, the acceleration they measure for a third
particle is the same provided vrel is constant. Begin with
vB = vA - vrel
Galileo’s Law of
Transformation of Velocities

If observers are moving but not
accelerating relative to each other,
they agree on a third object’s
acceleration, but not its velocity!
Inertial Reference Frames



Frames of reference which may move
relative to each other but in which
observers find the same value for the
acceleration of a third moving particle.
Inertial reference frames are moving at
constant velocity relative to each other. It
is impossible to identify which one may be
at rest.
Newton’s Laws hold only in inertial
reference frames, and do not hold in
reference frames which are accelerating.
Sample problem: How long does it take an automobile traveling in the left
lane at 60.0km/h to pull alongside a car traveling in the right lane at 40.0 km/h
if the cars’ front bumpers are initially 100 m apart?
Sample problem: A pilot of an airplane notes that the compass indicates a
heading due west. The airplane’s speed relative to the air is 150 km/h. If there
is a wind of 30.0 km/h toward the north, find the velocity of the airplane
relative to the ground.