Download Parallels and Euclidean Geometry Lines l and m which are coplanar

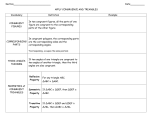
Parallels and Euclidean Geometry
Lines l and m which are coplanar but do not meet
are said to be parallel; we denote this by writing
l||m. Likewise, segments or rays are parallel if
they are subsets of parallel lines.
€
Given any two lines m and n, any third line l that
meets both m and n in distinct points is called a
transversal. This configuration makes a total of 8
angles with l, four with m and another four with n.
Let l and m meet at A and let l and n meet at B.
Any one of the angles at A is said to be alternate
with respect to any angle at B that lies on the
opposite side of l. Either of the two angles at A
whose sides include B are called interior angles, as
are either of the two angles at B whose sides
contain A; the other four angles are exterior
angles of the configuration. Finally, any two of
these angles not at the same vertex and on the
same side of l which are not both interior angles or
both exterior angles are said to be corresponding
angles.
A central story in the history of geometry is the
reaction to the manner in which Euclid developed
the concept of parallelism in his Elements. A study
of Book I shows that the first 28 Propositions were
developed in absolute geometry; this was
Proposition 28:
Theorem If two coplanar lines are cut by a
transversal so that some pair of alternate interior
angles are congruent, then the two lines are
parallel. //
Proposition i.29 is the converse of this theorem, but
it is not a theorem of absolute geometry: to prove it,
Euclid made use of a new axiom, his last and Fifth
Postulate: If two coplanar lines are cut by a
transversal so that some pair of interior angles on
the same side of the transversal have total measure
less than 180, then the two lines meet on that side of
the transversal. This postulate is effectively
equivalent to Proposition i.29: If two coplanar
parallel lines are cut by a transversal, then both
pairs of alternate interior angles are congruent.
Following Euclid, we will also add a new axiom to
absolute geometry which is logically equivalent to,
but simpler than, the Fifth Postulate. It was
formulated by the Greek geometer Proclus in the
5th century CE, but is more often attributed to
John Playfair (the Scottish geometry professor who
in 1795 published a classroom edition of the
Elements with this variant replacing the Fifth
Postulate).
[P-1] For any line l and point P not on l, there
exists in the same plane as l and P a unique
line passing through P and parallel to l.
Theorem If two coplanar parallel lines are cut by
a transversal, then both pairs of interior angles on
the same side of the transversal have total measure
equal to 180. //
From this we deduce a number of useful
transversal properties. (See Figure 4.7, p. 215, for
an explanation of why they have these names.)
Corollary [The C Property] If two coplanar lines
are cut by a transversal, then they are parallel if
and only if some pair of interior angles on the same
side of the transversal are supplementary. //
Corollary [The F Property] If two coplanar lines
are cut by a transversal, then they are parallel if
and only if some pair of corresponding angles are
congruent. //
Corollary [The Z Property] If two coplanar lines
are cut by a transversal, then they are parallel if
and only if some pair of alternate interior angles
are congruent. //
Theorem Parallelism is an equivalence relation
on the set of all lines. //
Theorem [The Exterior Angle Theorem] The
measure of any exterior angle of a triangle equals
the sum of the measures of the two opposite interior
angles. //
Corollary [Euclidean Triangle Angle Sums]
The angle sum of any triangle is 180. //
Theorem [The Midpoint Connector Theorem]
The segment joining the midpoints of two sides of a
triangle is parallel to the third side and has half
the length. //
A convex quadrilateral is called a parallelogram if
both pairs of opposite sides are parallel, a rhombus
if, in addition, some pair of adjacent sides are
congruent, and a square if also one of its interior
angles is right.
Theorem Either diagonal of a parallelogram
divides it into two congruent triangles. //
Corollary Both pairs of opposite sides of a
parallelogram are congruent. //
Corollary Any pair of adjacent angles in a
parallelogram are supplementary. //
Corollary If a convex quadrilateral has both pairs
of opposite sides congruent, it is a parallelogram. //
Corollary If a convex quadrilateral has a pair of
opposite sides congruent and parallel, it is a
parallelogram. //
Corollary The diagonals of a convex quadrilateral
bisect each other if and only if it is a parallelogram.
//
Theorem A parallelogram is a rhombus if and
only if its diagonals are perpendicular. //
Theorem A parallelogram is a rectangle if and
only if its diagonals are congruent. //
Theorem A parallelogram is a square if and only
if its diagonals are perpendicular and congruent. //
A trapezoid is a convex quadrilateral having one
pair of opposite sides, called the bases, parallel to
each other. The other pair of opposite sides are
called its legs. (Note that all parallelograms are
trapezoids.) The median of a trapezoid is the
segment joining the midpoints of its legs.
Theorem [The Midpoint Connector Theorem
for Trapezoids] A line parallel to the bases of a
trapezoid that bisects one leg bisects the other;
conversely, the median of a trapezoid is parallel to
its bases. Further, the length of the median is the
average of the lengths of the bases. //