* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Emt 212/4 analog electronic ii Chapter 2: Op-amp
Loudspeaker wikipedia , lookup
Cellular repeater wikipedia , lookup
Power MOSFET wikipedia , lookup
Audio crossover wikipedia , lookup
Superheterodyne receiver wikipedia , lookup
Tektronix analog oscilloscopes wikipedia , lookup
Oscilloscope wikipedia , lookup
Surge protector wikipedia , lookup
Flip-flop (electronics) wikipedia , lookup
Phase-locked loop wikipedia , lookup
Index of electronics articles wikipedia , lookup
Oscilloscope types wikipedia , lookup
Audio power wikipedia , lookup
Wilson current mirror wikipedia , lookup
Regenerative circuit wikipedia , lookup
Voltage regulator wikipedia , lookup
Oscilloscope history wikipedia , lookup
Power electronics wikipedia , lookup
Analog-to-digital converter wikipedia , lookup
Negative feedback wikipedia , lookup
Transistor–transistor logic wikipedia , lookup
Two-port network wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Current mirror wikipedia , lookup
Integrating ADC wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Radio transmitter design wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Schmitt trigger wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Rectiverter wikipedia , lookup
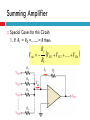
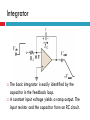
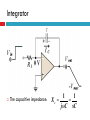
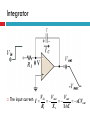
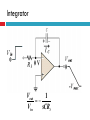
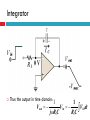
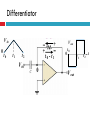
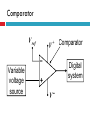
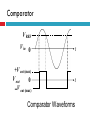
EMT 212/4 ANALOG ELECTRONIC II CHAPTER 2: OP-AMP APPLICATIONS & FREQUENCY RESPONSE Content 1. 2. Op-amp Application Introduction Inverting Amplifier Non-inverting Amplifier Voltage Follower / Buffer Amplifier Summing Amplifier Differencing Amplifier Integrator Differentiator Comparator Summary Frequency Response Op-amp Application Introduction Op-amps are used in many different applications. We will discuss the operation of the fundamental opamp applications. Keep in mind that the basic operation and characteristics of the op-amps do not change — the only thing that changes is how we use them Inverting Amplifier Circuit consists of an op-amp and three resistors. The positive (+) input to the op-amp is grounded through R2. The negative (-) input is connected to the input signal (via R1) and also to the feedback signal from the output (via RF). Inverting Amplifier V V+ Assume that amplifier operates in its linearly amplifying region. For an ideal op-amp, the difference between the input voltages V+ and V to the op-amp is very small, essentially zero; V V 0 V V Inverting Amplifier V V+ Hence; Vin V Vin iin R1 R1 Inverting Amplifier The op-amp input resistance is large, so the current into the +ve and –ve op-amp inputs terminal will be small, essentially zero V Vout iin RF V Vout Vin V RF R1 V 0 Vout Vin RF R1 Vout RF Av Vin R1 Inverting Amplifier Currents and voltages in the inverting op-amp Inverting Amplifier - Example Design an inverting amplifier with a specified voltage gain. Specification: Design the circuit such that the voltage gain is Av = -5. Assume the op-amp is driven by an ideal sinusoidal source, vs = 0.1sin wt (V), that can supply a maximum current of 5 µA. Assume that frequency w is low so that any frequency effects can be neglected. Non-Inverting Amplifier Circuit consists of an op-amp and three resistors. The negative (-) input to the op-amp is grounded through R1 and also to the feedback signal from the output (via RF). The positive (+) input is connected to the input signal. Non-Inverting Amplifier Input current to opamp is very small. No signal voltage is created across R2 and hence V vin V V so it follows that; V vin Non-Inverting Amplifier I 0 so RF and R1 carry the same current. Hence vout is related to V through a voltage-divider relationship R1 V vout R1 RF R1 vin vout R1 RF vout RF Av 1 vin R1 Non-Inverting Amplifier The output has the same polarity as the input, a positive input signal produces a positive output signal. The ratio of R1 and RF determines the gain. When a voltage is applied to the amplifier, the output voltage increases rapidly and will continue to rise until the voltage across R1 reaches the input voltage. Thus negligible input current will flow into the amplifier, and the gain depends only on R1 and RF Non-Inverting Amplifier The input resistance to the non-inverting amplifier is very high because the input current to the amplifier is also the input current to the op-amp, I+, which must be extremely small. Non-Inverting Amplifier v1 v2 v1 i1 R1 v1 vo i2 R2 i1 i2 v1 vo v1 R1 R2 vout R2 Av 1 vin R1 Voltage Follower / Buffer Amplifier This “buffer” is used to control impedance levels in the circuit – it isolates part of the overall (measurement) circuit from the output (driver). The input impedance to the buffer is very high and its output impedance is low. The output voltage from a source with high output impedance can, via the buffer, supply signal to one or more loads that have a low impedance. Voltage Follower / Buffer Amplifier High input impedance. Low output impedance. Voltage gain = 1 Vout Vin Vout Av 1 Vin Summing Amplifier The inverting amplifier can accept two or more inputs and produce a weighted sum. Using the same reasoning as with the inverting amplifier, that V ≈ 0. The sum of the currents through R1, R2,…,Rn is: Vn V1 V2 iin ... R1 R2 Rn Summing Amplifier The op-amp adjusts itself to draw iin through Rf (iin = if). if iin Vout iin R f Rf Rf Rf V1 V2 ... VN R2 RN R1 The output will thus be the sum of V1,V2,…,Vn, weighted by the gain factors, Rf/R1 , Rf/R2 ….., Rf/Rn respectively. Summing Amplifier Special Cases for this Circuit: 1. If R1 = R2 =……= R then: Vout Rf R1 VIN1 VIN 2 ..... VINn if iin Summing Amplifier 2. If R1 = R2 = … = R and VIN1, VIN2, … are either 0V (digital “0”) or 5V (digital “1”) then the output voltage is now proportional to the number of (digital) 1’s input. if iin Summing Amplifier - Application Digital to Analog Converter - binary-weighted resistor DAC Summing Amplifier - Application Digital to Analog Converter - R/2R Ladder DAC Differencing Amplifier This circuit produces an output which is proportional to the difference between the two inputs vout Rf R1 v1 v 2 Differencing Amplifier The circuit is linear so we can look at the output due to each input individually and then add them (superposition theorem) Differencing Amplifier Set v1 to zero. The output due to v2 is the same as the inverting amplifier, so v out 2 Rf R1 v2 Differencing Amplifier The signal to the non-inverting output, is reduced by the voltage divider: v in Rf R1 R f v1 Differencing Amplifier The output due to this is then that for a non-inverting amplifier: vout 1 Rf 1 R1 v in Differencing Amplifier v in Rf R1 R f Rf vout 1 1 R1 v1 v in Rf v out 1 1 R1 Rf v1 vout 1 R1 R f R R f 1 v1 Differencing Amplifier Rf vout 1 R1 v1 Thus the output is: v out 2 vout vout 1 vout 2 Rf R1 Rf R1 v2 v1 v2 Thus the amplifier subtracts the inputs and amplifies their difference. Integrator The basic integrator is easily identified by the capacitor in the feedback loop. A constant input voltage yields a ramp output. The input resistor and the capacitor form an RC circuit. Integrator The slope of the ramp is determined by the RC time constant. The integrator can be used to change a square wave input into a triangular wave output. Integrator The capacitive impedance: 1 1 Xc jC sC Integrator The input current: I Vin Vout Vout sCVout Ri Xc 1 /sC Integrator Vout 1 Vin sCRi Integrator Thus the output in time domain: 1 Vout 1 Vin Vindt jRi C Ri C Differentiator V in 0 t0 t1 + t2 V in 0 + t0 - t1 V out 0 t0 t1 V out t2 t Differentiator The differentiator does the opposite of the integrator in that it takes a sloping input and provides an output that is proportional to the rate of change of the input. Note the capacitor is in the input circuit. The output voltage can be determined by the formula below: Vout dVin R Vin RC 1 dt jC Comparator The comparator is an op-amp circuit that compares two input voltages and produces an output indicating the relationship between them. The inputs can be two signals (such as two sine waves) or a signal and a fixed dc reference voltage. Comparators are most commonly used in digital applications. Comparator Digital circuits respond to rectangular or square waves, rather than sine waves. These waveforms are made up of alternating (high and low) dc levels and the transitions between them. Transitions "High" dc level "Low" dc level Comparator Example: Assume that the digital system is designed to perform a specific function when a sine wave input reaches a value of 10 V Comparator V ref V + Variable voltage source Comparator Digital system V Comparator With nonzero-level +V detection the voltage divider or zener R diode sets the reference voltage atV Z which the op-amp turns goes to the maximum voltage level. V out + V in (c) Zener diode sets reference voltage Comparator V REF V in 0 t +V out (max) V out 0 V out (max) t Comparator Waveforms Comparator Remember that the comparator is configured in open-loop, making the gain very high. This is open-loop configuration. This makes the comparator very susceptible to unwanted signals (noise) that could cause the output to arbitrarily switch states. Comparator If the level of the pulse must be less than the output of a saturated op-amp, a zener-diode can be used to limit the output to a particular voltage. This is called output bounding. Either positive, negative, or both halves of the output signal can be bounded by use of one or two zener diodes respectively D1 D2 0 +V Z 2 + 0.7 V V in R i 0 V Z 2 0.7 V Comparator - Application Over-Temperature Sensing circuit Comparator - Application Analog to Digital Converter Summary The summing amplifier’s output is the sum of the inputs. An averaging amplifier yields an output that is the average of all the inputs. The scaling adder has inputs of different weight with each contributing more or less to the input. Integrators change a constant voltage input to a sloped output. Differentiators change a sloping input into a step voltage proportional to the rate of change. The op-amp comparator’s output changes state when the input voltage exceeds the reference voltage. Frequency Response of Op-amp The “frequency response” of any circuit is the magnitude of the gain in decibels (dB) as a function of the frequency of the input signal. The decibel is a common unit of measurement for the relative magnitude of two power levels. The expression for such a ratio of power is: Power level in dB = 10log10(P1/P2) Note: A decibel is one-tenth of a "Bel", a seldom-used unit named for Alexander Graham Bell, inventor of the telephone. Frequency Response of Op-amp The voltage or current gain of an amplifier expressed in dB is 20 log10|A|, where A = Vout/Vin. The frequency response of an op-amp has a low-pass characteristic (passing low-frequency signals, attenuating highfrequency signals). Gain (log scale) A -3 dB point fc Freq (Hz) Frequency Response of Op-amp The bandwidth is the frequency at which the power of the output signal is reduced to half that of the maximum output power. This occurs when the power gain A drops by 3 dB. In Figure shown before, the bandwidth is fc Hz. For all op-amps, the Gain*Bandwidth product is a constant. Hence, if the gain of an op-amp is decreased, its operational bandwidth increases proportionally.