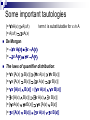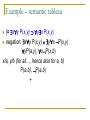Download A(x)

Lesson 6
Semantics of FOPL
Interpretation, models,
semantic tableau
4/30/2017
FOPL: Interpretation, models
1
Truth of a formula, interpretation,
evaluation
We have seen (in Lesson 4) that the question

“Is a formula A true?”
is reasonable only when we add


“in the interpretation I for a valuation v of free variables”.
Interpretation structure is an n-tuple:
I = U, R1,...,Rn, F1,...,Fm,
where F1,...,Fm are functions over the universe of discourse assigned
to the functional symbols occurring in the formula, and
R1,...,Rn are relations over the universe of discourse assigned to the
predicate symbols occurring in the formula.
How to evaluate the truth-value of a formula in an
interpretation structure I, or for short in the Interpretation I?
4/30/2017
FOPL: Interpretation, models
2
Interpretation, evaluation of a formula

We evaluate bottom up, i.e., from the “inside out” :
A.
B.
C.
A.
First, determine the elements of the universe denoted by terms,
then determine the truth-values of atomic formulas, and
finally, determine the truth-value of the (composed) formula
Evaluation of terms:
Let v be a valuation that associates each variable x with an
element of the universe: v(x)  U.
By evaluation e of terms induced by v we obtain an
element e(x) of the universe U that is defined inductively as
follows:
e(x) = v(x)
e(f(t1, t2,...,tn)) = F(e(t1), e(t2),...,e(tn)),
where F is the function assigned by I to the functional
symbol f.
4/30/2017
FOPL: Interpretation, models
3
Interpretation, evaluation of a formula
B. Evaluation of a formula
1. Atomic formulas: |=I P(t1,...,tn)[v] – the formula is true in
the interpretation I for a valuation v iff
e(t1), e(t2),...,e(tn)  R,
where R is the relation assigned to the symbol P
(we also say that R is the domain of truth of P)
2. Composed formulas:
Propositionally composed A, A  B, A  B, A  B, A  B,
dtto Propositional Logic
b)
Quantified Formulas xA(x), xA(x):
|=I xA(x)[v], if for any individual i  U holds |=I A[v(x/i)],
where v(x/i) is a valuation identical to v up to
assigning the individual i to the variable x
|=I xA(x)[v], if for at least one individual i  U holds |=I A[v(x/i)].
a)
4/30/2017
FOPL: Interpretation, models
4
Quantifiers
It is obvious from the definition of quantifiers that over a
finite universe of discourse U = {a1,…,an} the
following equivalences hold:
 x A(x)  A(a1)  …  A(an)
 x A(x)  A(a1)  …  A(an)
Hence the universal quantifier is a generalization of a
conjunction; existential quantifier is a generalization
of a disjunction.
Therefore, the following obviously holds:
 x A(x)  x A(x), x A(x)  x A(x)
de Morgan laws
4/30/2017
FOPL: Interpretation, models
5
Satisfiability and validness in interpretation






Formula A is satisfiable in interpretation I, if there exists
valuation v of variables that |=I A[v].
Formula A is true in interpretation I, |=I A, if for all possible
valuations v holds that |=I A[v].
Model of formula A is interpretation I, in which is A true
(that means for all valuations of free variables).
Formula A is satisfiable, if there is interpretation I, in which
A is satisfied (i.e., if there is an interpretation I and valuation v
such that |=I A[v].)
Formula A is a tautology (logically valid), |= A, if A is true in
every interpretation (i.e., for all valuations).
Formula A is a contradiction, if there is no interpretation I,
that would satisfy A, so there is no interpretation and
valuation, in which A would be true: |I A[v], for any I and v.
Satisfiability and validness in interpretation



A: x P(f(x), x)
B: x P(f(x), x)
C: P(f(x), x)
Interpretation I: U=N, f  x2, P  relation >
It is true that: |=I B. Formula B is in N, x2, > true.
Formulas A and C are in N, >, x2 satisfied, but not
true:
e0(x) = 0, e1(x) = 1 these 0,0, 1,1 are not the
elements of >, but for e2(x) = 2, e3(x) = 3, … the couples
are 4,2, 9,3, … the elements of relation >.
 for

Formulas A, C are not in N, x2, > true:
|I A[e0], |I A[e1], |I C[e0], |I C[e1],
only:
|=I A[e2], |=I A[e3], |=I C[e2], |=I C[e3], …
Empty universum?


Consider an empty universe U = 
x P(x): is it true or not?





By the definition of quantifiers it is false, because we can’t find any
individual which would satisfy P, then it is true that x P(x), so
x P(x), but this is false as well – contradiction.
Or it is true, because there is no element of the universe that would
not have the property P, but then x P(x) should be true as well,
which is false – contradiction.
Likewise for x P(x) leads to a contradiction
So we always choose a non-empty universe of
interpretation
Logic “of an empty world” would not be not
reasonable
Existential quantifier + implication?



There is somebody such that if he/she is a genius,
then everybody is a genius.
This sentence cannot be false: |= x (G(x)  xG(x))
For every interpretation I it holds:


If the truth-domain GU of the predicate G is equal to the
whole universe (GU = U), then the formula is true in I,
because the subformula xG(x) is true;
hence G(x)  x G(x), and x (G(x)  xG(x)) is true in I.
If GU is a proper subset of U (GU  U), then it suffices to find
at least one individual a (assigned by valuation v to x) such
that a is not an element of GU. Then G(a)  x G(x) is true in
I, because the antecedent G(a) is false. Hence
x (G(x)  xG(x)) is true in I.
9
Existential quantifier + conjunction !

Similarly x (P(x)  Q(x)) is “almost” a tautology. It
is true in every interpretation I such that






PU  U, because then |=I P(x)  Q(x)[v] for v(x)  PU
or QU = U, because then |=I P(x)  Q(x) for all valuations
So this formula is false only in such an
interpretation I where PU = U and QU  U.
Therefore, sentences of a type
“Some P’s are Q’s”
are analyzed by x (P(x)  Q(x)).
Universal quantifier + conjunction?
Usually no, but implication!





Similarly x [P(x)  Q(x)] is ”almost” a contradiction!
The formula is false in every interpretation I such that
PU  U or QU  U.
So the formula is true only in an interpretation I such that
PU = U a QU = U
Therefore, sentences of a type
“All P’s are Q’s“
are analyzed by x [P(x)  Q(x)]
It holds for all individuals x that if x is a P then x is a Q.
(See the definition of the subset relation PU  QU)
Satisfiability and validness in interpretation
Formula A(x) with a free variable x:
 If A(x) is true in I, then |=I x A(x)
 If A(x) is satisfied in I, then |=I x A(x).
Formulas P(x)  Q(x), P(x)  Q(x)
with the free variable x define the intersection and
union, respectively, of truth-domains PU, QU. For
every P, Q, PU, QU and an interpretation I it holds:
|=I x [P(x)  Q(x)]
iff
PU  QU
|=I x [P(x)  Q(x)]
iff
PU  QU  
|=I x [P(x)  Q(x)]
iff
PU  QU = U
|=I x [P(x)  Q(x)]
iff
PU  QU  
Model of a set of formulas, logical entailment





A Model of the set of formulas {A1,…,An} is an
interpretation I such that each of the formulas A1,...,An is
true in I.
Formula B logically follows from A1, …, An, denoted
A1,…,An |= B, iff B is true in every model of {A1,…,An}.
Thus for every interpretation I in which the formulas A1, …,
An are true it holds that the formula B is true as well:
A1,…,An |= B: If |=I A1,…, |=I An then |=I B, for all I.
Note that the “circumstances“ under which a formula is, or
is not, true (see the 1st lesson, Definition 1) are in FOPL
modelled by interpretations (of predicates and functional
symbols by relations and functions, respectively, over the
universe).
Logical entailment in FOPL
P(x) |= x P(x),
but the formula P(x)  x P(x) is obviously not a tautology.
Therefore, A1,...,An |= Z  |= (A1… An  Z) holds in FOPL only
for closed formulas, so-called sentences.
 x P(x)  P(a) is also not a tautology, and thus the rule
x P(x) | P(a) is not truth-preserving;
 P(a) does not logically follow form x P(x).
 Example of an interpretation I such that x P(x) is, and P(a) is
not true in I:
U = N(atural numbers), P  even numbers, a  3

Semantic verification of an argument
An argument is valid iff the conclusion is true
in every model of the set of the premises.
 But the set of models can be infinite!
 And, of course, we cannot examine an infinite
number of models; but we can verify the
‘logical form’ of the argument, and check
whether the models of premises do satisfy the
conclusion.

Semantic verification of an argument

Example:

All monkeys (P) like bananas (Q)
 Judy (a) is monkey
  Judy likes bananas
x [P(x)  Q(x)]
P(a)
-------------------Q(a)
QU
PU
a
Relations



Propositions with unary predicates (expressing
properties of individuals) were studied already in
the ancient times by Aristotle.
Until quite recently Gottlob Frege, the founder of
modern logic, developed the system of formal
predicate logic with n-ary predicates characterizing
relations between individuals, and with quantifiers.
Frege, however, used another language than the
one of the current FOPL.
Aristotle:
(384 BC – March 7, 322 BC)




a Greek philosopher, a student of
Plato and teacher of Alexander the
Great.
He wrote on diverse subjects,
including physics, metaphysics,
poetry (including theater), biology
and zoology, logic, rhetoric, politics,
government, and ethics.
Along with Socrates and Plato,
Aristotle was one of the most
influential of the ancient Greek
philosophers. They transformed
Presocratic Greek philosophy into
the foundations of Western
philosophy as we know it.
Plato and Aristotle have founded two
of the most important schools of
Ancient philosophy.
Gottlob Frege
1848 – 1925
German
mathematician,
logician and
philosopher,
taught at the
University of
Jena.
Founder of modern
logic.
19
Semantic verification of an argument




Marie likes only winners
Karel is a winner
------------------------------------- Marie likes Karel
invalid
x [R(m,x)  V(x)], V(k)  R(m,k) ?
RU  U  U: {… <Marie, i1>, <Marie, i2>, …, <Marie, in> …}
 VU  U:
{…i1, i2, …, Karel,…, in…}
The pair <Marie, Karel> doesn’t have to be an elements of
RU, it is not guaranteed by the validity of the premises.
Being a winner is only a necessary condition for Marie’s liking
somebody, but it is not a sufficient condition.

Semantic verification of an argument




Marie likes only winners
Karel is not a winner
------------------------------------ Marie does not like Karel
valid
x [R(m,x)  V(x)], V(k)  R(m,k)

RU  U  U:
{…<Marie, i1>, <Marie, i2>, <Marie, Karel>, …, <Marie, in> …}

VU  U:
{…i1, i2, …, Karel, Karel,…, in…}
Let the pair <Marie, Karel> be an element of RU;
then by the first premise Karel has to be an element of VU, but
it is not so if the second premise is true.
Hence the pair <Marie, Karel> is not an element of RU.
The validity of the conclusion is guaranteed by the validity of premises.
Semantic verification of an
argument
Anybody who knows Marie and Karel
is sorry for Marie.
Some are not sorry for Marie
though they know her.
|= Somebody knows Marie but not Karel.


x [(K(x,m)  K(x,k))  S(x,m)]
x [S(x,m)  K(x,m)]
x [K(x,m)  K(x,k)]
We illustrate the truth-domain of predicates K and S, i.e., the relations
KU and SU that satisfy the premises:
KU = {…, i1,m,  i1,k, i2,m, i2,k,…, ,m,… }
1. premise

SU = {…, i1,m, ...., i2,m,…........., ,m,… }
2. premise
Semantic verification of an argument:
an indirect proof
Anybody who knows Marie and Karel
is sorry for Marie.
Some are not sorry for Marie
though they know her.
x [(K(x,m)  K(x,k))  S(x,m)]
x [S(x,m)  K(x,m)]
|= Somebody knows Marie but not Karel. x [K(x,m)  K(x,k)]

Assume now that all the individuals who are paired with m in KU
are also paired with k in KU:

KU = {…, i1,m,  i1,k, i2,m, i2,k,…, ,m, ,k … }

SU = {…, i1,m, ...., i2,m,…........., ,m, ,m … }
contradiction
Some important tautologies


|= xAx  Ax/t
term t is substitutable for x in A
|= Ax/t  xAx
De Morgan
|= x Ax  x Ax
|= x Ax  x Ax
The laws of quantifier distribution:
|= x [A(x)  B(x)]  [x A(x)  x B(x)]
|= x [A(x)  B(x)]  [x A(x)  x B(x)]
|= x [A(x)  B(x)]  [x A(x)  x B(x)]
|= x [A(x)  B(x)]  [x A(x)  x B(x)]
|= [xA(x)  xB(x)]  x [A(x)  B(x)]
|= x [A(x)  B(x)]  [x A(x)  x B(x)]
Semantic proofs:
Let AU, BU be truth-domains of A, B
x[A(x)  B(x)]  [xA(x)  xB(x)]
If the intersection (AU  BU) = U, then AU and BU must be equal to the
whole universe U, and vice-versa.
x[A(x)  B(x)]  [xA(x)  xB(x)]
If the union (AU  BU)  , then AU or BU must be non-empty (AU  ,
or BU  ), and vice-versa.
|= x[A(x)  B(x)]  [xA(x)  xB(x)]
If AU  BU, then if AU = U then BU = U.
|= x[A(x)  B(x)]  [xA(x)  xB(x)]
If AU  BU, then if AU   then BU  .
|= x[A(x)  B(x)]  [xA(x)  xB(x)]
If the intersection (AU  BU)  , then AU and BU must be non-empty
(AU  , BU  ).
|= [xA(x)  xB(x)]  x[A(x)  B(x)]
If AU = U or BU = U, then the union (AU  BU) = U
Some important tautologies

Formula A does not contain free variable x:
|= x[A  B(x)]  [A  xB(x)]
|= x[A  B(x)]  [A  xB(x)]
|= x[B(x)  A]  [xB(x)  A]
|= x[B(x)  A]  [xB(x)  A]
|= x[A  B(x)]  [A  xB(x)]
|= x[A  B(x)]  [A  xB(x)]
|= x[A  B(x)]  [A  xB(x)]
|= x[A  B(x)]  [A  xB(x)]

The commutative law of quantifiers.
|= xyA(x,y)  yxA(x,y)
|= xyA(x,y)  yxA(x,y)
|= xyA(x,y)  yxA(x,y)
but not vice-versa!
Semantic proofs: Let AU, BU be truthdomains of A, B, x is not free in A
x[A  B(x)]  [A  xB(x)] – obvious
x[A  B(x)]  [A  xB(x)] – obvious
x [B(x)  A]  [x B(x)  A]
x [B(x)  A]  x [B(x)  A]: the complement BU or
A is the whole universe: x B(x)  A 
x B(x)  A  x B(x)  A
x[B(x)  A]  [xB(x)  A]
x [B(x)  A]  x [B(x)  A]: the complement BU is
non-empty or A: x B(x)  A 
x B(x)  A  x B(x)  A
Semantic tableau in
predicate logic
Proofs of logical validity and
argument validity in 1st-order
predicate logic
Typical problems

Prove the logical validity of a formula:



A formula F is true in all interpretations, which means
that every interpretation is a model
|= F
Prove the validity of an argument:
P1, …, Pn |= Q
 for close formulas iff |= (P1 … Pn  Q)
 formula Q is true in all the models of the set of premises
P1, …, Pn


What is entailed by the given premises?

P1, …, Pn |= ?
Typical problems
Semantic solution over an infinite set of
models is difficult, semantics proofs are tough.
 So we are trying to find some other methods
 One of them is the semantic-tableau method.
 Analogy, generalization of the same method in
propositional logic
 Transformation to a disjunctive / conjunctive
normal form.

Semantic tableau in FOPL







When proving a tautology by
a direct proof – we use a conjunctive normal form
an indirect proof– disjunctive normal form
In order to apply the propositional logic method of
semantic tableau, we have to get rid of quantifiers.
How to eliminate them?
To this end we use the following rules:
x A(x) | A(x/t), where t is a term which is
substitutable for x in A, usually t = x
(x)A(x) | A(a), where a is a new constant (not
used in the proof as yet)
Rules for quantifiers elimination



x A(x) | A(x/t), term t is substitutable for x
 If the truth-domain AU = U, then the individual e(t) is an element of
AU
 The rule is truth-preserving, OK
(x)A(x) | A(a), where a is a new constant
 If the truth-domain AU  , the individual e(a) might not be an
element of AU
 The rule is not truth-preserving!
x (y) B(x,y) | B(a, b), where a, b are suitable constants
 Though if for every x there is a y such that the pair <x,y> is in BU,
the pair <a, b> might not be an element of BU.
 The rule is not truth-preserving!


However, existential-quantifier elimination does not yield a contradiction: it
is possible to interpret the constants a, b so that the formula on the righthand side is true, whenever the formula on the left-hand side is true.
For this reason we use the indirect proof (disjunctive tableau), whenever
the premises contain existential quantifier(s)
Semantic tableau in FOPL– disjunctive




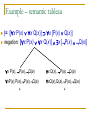
Example. Proof of the logical validity of a formula:
|= x [P(x)  Q(x)]  [x P(x)  x Q(x)]
Indirect proof (non-satisfiable of formula):
x [P(x)  Q(x)]  x P(x)  x Q(x)
(order!)
2.
3.
1.
x [P(x)  Q(x)], P(a)  Q(a), P(a), Q(a)
x [P(x)  Q(x)], P(a), P(a), Q(a)
x [P(x)  Q(x)], Q(a), P(a), Q(a)
+
+
Both branches are closed, they are contradictory. Therefore, the
original (blue) formula is tautology.
Semantic tableau


|=? x [P(x)  Q(x)]  [x P(x)  x Q(x)]
Negation:
x [P(x)  Q(x)]  x P(x)  x Q(x)
x [P(x)  Q(x)], P(a), Q(b)
P(a)  Q(a), P(b)  Q(b), P(a), Q(b)
P(a), P(b)  Q(b), P(a), Q(b)
1.eliminaton  - diff. const. !
2. elimination 
Q(a), P(b)  Q(b), P(a), Q(b)
P(a), P(b), P(a), Q(b) P(a), Q(b), P(a), Q(b)
Q(a), P(b), P(a), Q(b)
Q(a), Q(b), P(a), Q(b)
Formula is not logically valid, 3. branch is not closed
Tableau can lead to an infinite evaluation
F: x y P(x,y)  x P(x,x) 
x y z ([P(x,y)  P(y,z)]  P(x,z))
 Variable x is bound by universal quantifier
 We must “check all x” : a1, a2, a3, …
 For y we must choose always another constant:
P(a1, a2), P(a1, a1)
P(a2, a3), P(a2, a2), P(a2, a1)
P(a3, a4), P(a3, a3), P(a3, a2)
P(a4, a5), P(a4, a4), P(a4, a3)
…
The problem of logical validity is not decidable in
FOPL

Tableau can lead to an infinite evaluation



1.
2.
F: x y P(x,y)  x P(x,x) 
x y z ([P(x,y)  P(y,z)]  P(x,z))
What kind of formula is F? Is it satisfiable, contradictory or logicaly
valid?
Try to find a model:
U=N
PU = relation < (less then)
1 2 3 4 5 ...
satisfiable
Could the formula F have a finite model?
U = {a1, a2, a3, ... ? }
To a1 there must exist an element a2, so that P(a1, a2), a2  a1
To a2 there must exist an element a3 such that P(a2, a3), a3  a2, and a3
 a1 otherwise P(a1, a2)  P(a2, a1), so P(a1, a1).
To a3 there must exist an element a4 such that P(a3, a4), a4  a3, and a4 
a2 otherwise P(a2, a3)  P(a3, a2), so P(a2, a2).
And so on ad infinitum…
Argument validity- indirect proof
x [P(x)  Q(x)]  x Q(x) |= x P(x)
 x [P(x)  Q(x)], x Q(x), x P(x) – contradictory?
x [P(x)  Q(x)], Q(a), x P(x)
x [P(x)  Q(x)], x P(x), [P(a)  Q(a)], Q(a),
P(a)
P(a), Q(a), P(a)
Q(a), Q(a), P(a)
+
+

Both branches are closed. The set of premises together
with the negated conclusion is contradictory; so the
argument is valid…
Argument validity- indirect proof
x [P(x)  Q(x)]  x Q(x) |= x P(x)
No whale is fish.
The fish exists.
-------------------------------------------Some individuals are not the whales.
 The set of statements: {No whale is fish, but
fish exists, All individuals are whales} is
contradictory.

Consistency checking
There is a barber who shaves just those who do
not shave themselves
 Does the barber shave himself?
 x y [H(y,y)  H(x,y)] |= ?
H(y,y)  H(a,y), H(y,y)  H(a,y) – eliminating 
H(a,a)  H(a,a), H(a,a)  H(a,a) – eliminating 
H(a,a), H(a,a)  H(a,a), H(a,a), H(a,a)  H(a,a)
H(a,a), H(a,a)
H(a,a), H(a,a) …
+
The first sentence is contradictory; anything is
entailed by it. But, such a barber does not exist.

Summary – semantic tableau in FOPL






We use semantic tableaus for an indirect proof, i.e., transform a formula
to the disjunctive normal form
(branching means disjunction, comma conjunction)
There is a problem with closed formulas. We need to eliminate
quantifiers.
First, eliminate existential quantifiers: replace the variable (which is not in
the scope of any universal quantifier) by a new constant that is still not
used.
Second, eliminate universal quantifiers: replace the universally bound
variables step by step by suitable constants, until a contradiction
emerges, i.e., the branch gets closed
If a variable x is bound by an existential quantifier and x is in the scope of
a universal quantifier binding a variable y, we must gradually replace y by
suitable constants and consequently the variable x by new, not used
constants …
If the tableau eventually gets closed, the formula or a set of formulas is
contradictory.
Example – semantic tableau
|= xy P(x,y)  yx P(x,y)
 negation: xy P(x,y)  yx P(x,y)
yP(a,y), xP(x,b)
x/a, y/b (for all…, hence also for a, b)
P(a,b), P(a,b)
+

Example – semantic tableau


|= [x P(x)  x Q(x)]  x [P(x)  Q(x)]
negation: [x P(x)  x Q(x)]  x [P(x)  Q(x)]
x P(x), P(a), Q(a)
x Q(x), P(a), Q(a)
xP(x),P(a),P(a),Q(a)
+
xQ(x),Q(a),P(a),Q(a)
+
Gottlob Frege






Friedrich Ludwig Gottlob Frege (b. 1848, d. 1925) was a German
mathematician, logician, and philosopher who worked at the University of
Jena.
Frege essentially reconceived the discipline of logic by constructing a
formal system which, in effect, constituted the first ‘predicate calculus’. In
this formal system, Frege developed an analysis of quantified statements
and formalized the notion of a ‘proof’ in terms that are still accepted today.
Frege then demonstrated that one could use his system to resolve
theoretical mathematical statements in terms of simpler logical and
mathematical notions. Bertrand Russell showed that of the axioms that
Frege later added to his system, in the attempt to derive significant parts of
mathematics from logic, proved to be inconsistent.
Nevertheless, his definitions (of the predecessor relation and of the
concept of natural number) and methods (for deriving the axioms of
number theory) constituted a significant advance. To ground his views about
the relationship of logic and mathematics, Frege conceived a
comprehensive philosophy of language that many philosophers still find
insightful. However, his lifelong project, of showing that mathematics was
reducible to logic, was not successful.
Stanford Encyclopedia of Philosophy
43
http://plato.stanford.edu/entries/frege/
Bertrand Russell


1872-1970
British philosopher, logician,
essay-writer
Bertrand Russell
Bertrand Arthur William Russell (b.1872 - d.1970) was
a British philosopher, logician, essayist, and social
critic, best known for his work in mathematical logic
and analytic philosophy. His most influential
contributions include his defense of logicism (the
view that mathematics is in some important sense
reducible to logic), and his theories of definite
descriptions and logical atomism. Along with G.E.
Moore, Russell is generally recognized as one of the
founders of analytic philosophy. Along with Kurt
Gödel, he is also regularly credited with being one
of the two most important logicians of the twentieth
century.
Kurt Gödel (1906-Brno, 1978-Princeton)
The greatest logician of 20th century, a friend of A. Einstein,
became famous by his Incompleteness Theorems of arithmetic
Russell's Paradox


Russell's paradox is the most famous of the
logical or set-theoretical paradoxes. The
paradox arises within naive set theory by
considering the set of all sets that are not
members of themselves. Such a set appears
to be a member of itself if and only if it is not
a member of itself, hence the paradox.
http://plato.stanford.edu/entries/russellparadox/
Russell's Paradox
Some sets, such as the set of all teacups, are not
members of themselves. Other sets, such as the set
of all non-teacups, are members of themselves. Call
the set of all sets that are not members of
themselves "R." If R is a member of itself, then by
definition it must not be a member of itself. Similarly,
if R is not a member of itself, then by definition it
must be a member of itself. Discovered by Bertrand
Russell in 1901, the paradox has prompted much
work in logic, set theory and the philosophy and
foundations of mathematics.
Russell's Paradox
R – the set of all normal sets that are not members of
themselves
Question: “Is R normal?” yields a contradiction.
 In symbols: xR  (xx) – by the definition of R
 The question R  R? yields a contradiction:
 RR  RR, because:
 Answer YES – R is not normal, RR, but by the
definition R is not a member of R, i.e. RR
 Answer NO – R is normal, RR, but then by the
definition RR
(because R is the set of all normal sets)
Russell wrote to Gottlob Frege with news of his
paradox on June 16, 1902. The paradox was of
significance to Frege's logical work since, in effect, it
showed that the axioms Frege was using to
formalize his logic were inconsistent.
Specifically, Frege's Rule V, which states that two sets
are equal if and only if their corresponding functions
coincide in values for all possible arguments,
requires that an expression such as f(x) be
considered both a function of the argument x and a
function of the argument f. In effect, it was this
ambiguity that allowed Russell to construct R in
such a way that it could both be and not be a
member of itself.
Russell's Paradox
Russell's letter arrived just as the second volume of Frege's Grundgesetze der
Arithmetik (The Basic Laws of Arithmetic, 1893, 1903) was in press.
Immediately appreciating the difficulty the paradox posed, Frege added to the
Grundgesetze a hastily composed appendix discussing Russell's discovery.
In the appendix Frege observes that the consequences of Russell's paradox
are not immediately clear. For example, "Is it always permissible to speak of
the extension of a concept, of a class? And if not, how do we recognize the
exceptional cases? Can we always infer from the extension of one concept's
coinciding with that of a second, that every object which falls under the first
concept also falls under the second? These are the questions," Frege notes,
"raised by Mr Russell's communication." Because of these worries, Frege
eventually felt forced to abandon many of his views about logic and
mathematics.
Of course, Russell also was concerned about the contradiction. Upon learning
that Frege agreed with him about the significance of the result, he
immediately began writing an appendix for his own soon-to-be-released
Principles of Mathematics. Entitled "Appendix B: The Doctrine of Types," the
appendix represents Russell's first detailed attempt at providing a principled
method for avoiding what was soon to become known as "Russell's paradox."
51
Russell's Paradox
The significance of Russell's paradox can be seen once it is realized that, using
classical logic, all sentences follow from a contradiction. For example, assuming both
P and ~P, any arbitrary proposition, Q, can be proved as follows: from P we obtain P
Q by the rule of Addition; then from P Q and ~P we obtain Q by the rule of Disjunctive
Syllogism. Because of this, and because set theory underlies all branches of
mathematics, many people began to worry that, if set theory was inconsistent, no
mathematical proof could be trusted completely.
Russell's paradox ultimately stems from the idea that any coherent condition may be used
to determine a set. As a result, most attempts at resolving the paradox have
concentrated on various ways of restricting the principles governing set existence
found within naive set theory, particularly the so-called Comprehension (or Abstraction)
axiom. This axiom in effect states that any propositional function, P(x), containing x as
a free variable can be used to determine a set. In other words, corresponding to every
propositional function, P(x), there will exist a set whose members are exactly those
things, x, that have property P. It is now generally, although not universally, agreed
that such an axiom must either be abandoned or modified.
Russell's own response to the paradox was his aptly named theory of types. Recognizing
that self-reference lies at the heart of the paradox, Russell's basic idea is that we can
avoid commitment to R (the set of all sets that are not members of themselves) by
arranging all sentences (or, equivalently, all propositional functions) into a hierarchy.
The lowest level of this hierarchy will consist of sentences about individuals. The next
lowest level will consist of sentences about sets of individuals. The next lowest level
will consist of sentences about sets of sets of individuals, and so on. It is then possible
to refer to all objects for which a given condition (or predicate) holds only if they are all
at the same level or of the same "type."
52
Russell’s paradox – 3 solutions
Russell's own response to the paradox was his aptly named theory of types.
Recognizing that self-reference lies at the heart of the paradox, Russell's basic
idea is that we can avoid commitment to R (the set of all sets that are not
members of themselves) by arranging all sentences (or, equivalently, all
propositional functions) into a hierarchy. The lowest level of this hierarchy will
consist of sentences about individuals. The next lowest level will consist of
sentences about sets of individuals. The next lowest level will consist of
sentences about sets of sets of individuals, and so on. It is then possible to
refer to all objects for which a given condition (or predicate) holds only if they
are all at the same level or of the same "type."
This solution to Russell's paradox is motivated in large part by the so-called
vicious circle principle, a principle which, in effect, states that no
propositional function can be defined prior to specifying the function's range. In
other words, before a function can be defined, one first has to specify exactly
those objects to which the function will apply. (For example, before defining the
predicate "is a prime number," one first needs to define the range of objects
that this predicate might be said to satisfy, namely the set, N, of natural
numbers.) From this it follows that no function's range will ever be able to
include any object defined in terms of the function itself. As a result,
propositional functions (along with their corresponding propositions) will end up
being arranged in a hierarchy of exactly the kind Russell proposes.
53
Russell’s paradox – 3 solutions
Although Russell first introduced his theory of types in his 1903 Principles of Mathematics,
type theory found its mature expression five years later in his 1908 article, "Mathematical
Logic as Based on the Theory of Types," and in the monumental work he co-authored
with Alfred North Whitehead, Principia Mathematica (1910, 1912, 1913). Russell's
type theory thus appears in two versions: the "simple theory" of 1903 and the "ramified
theory" of 1908. Both versions have been criticized for being too ad hoc to eliminate the
paradox successfully. In addition, even if type theory is successful in eliminating
Russell's paradox, it is likely to be ineffective at resolving other, unrelated paradoxes.
Other responses to Russell's paradox have included those of David Hilbert and the
formalists (whose basic idea was to allow the use of only finite, well-defined and
constructible objects, together with rules of inference deemed to be absolutely certain),
and of Luitzen Brouwer and the intuitionists (whose basic idea was that one cannot
assert the existence of a mathematical object unless one can also indicate how to go
about constructing it).
Yet a fourth response was embodied in Ernst Zermelo's 1908 axiomatization of set theory.
Zermelo's axioms were designed to resolve Russell's paradox by again restricting the
Comprehension axiom in a manner not dissimilar to that proposed by Russell. ZF and
ZFC (i.e., ZF supplemented by the Axiom of Choice), the two axiomatizations generally
used today, are modifications of Zermelo's theory developed primarily by Abraham
Fraenkel.
54