Download football_physical_Ma..

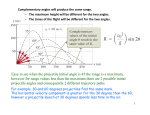
Newton’s Second Law
The acceleration of an object is directly proportional to the force acting on it. Thus, we
can relate mass, acceleration, and force through the following mathematical statement of
Newton’s second law: Sum of Forces = Mass x Acceleration
Newton’s Third Law
If two objects interact, the force F12 exerted by object 1 on object 2 is equal in magnitude
and opposite in direction to the force F21 exerted by object 2 on object 1: F12 = - F21
Laws of Motion
Pg. 138
Q: While a football is in flight, what are the forces that act on it?
A: While a football is in flight, the force of gravity and air resistance act on in it.
Q: What are the reaction pairs while the football is being kicked?
A: When a football is being kicked, the foot pushes forward on the ball and the ball
pushes backward on the foot.
Energy and Energy Transfer


Kinetic Energy is defined as the energy that a body or system has because of its
motion.
Kinetic energy of a particle of mass (m) moving with a speed (v) is:
K = (1/2)mv2
Instantaneous Power (P) is defined as the time rate of energy transfer. If an agent
apples a force (F) to an object moving with a velocity (v), the power delivered by
that agent is:
P=Fxv
Q: When a punter kicks a football, is he doing any work on the ball while his toe is in
contact with it? Is he doing any work on the ball after it loses contact with his toe? Are
any of forces doing work on the ball while it is in flight?
A: Yes. Force time distance over which the toe is in contact with the ball. No, he is no
longer applying a force. Yes, both friction and gravity do work.
Q: A 0.300 kg ball has a speed of 15.0 m/s (a) What is its kinetic energy? (b) What if? Its
speed were doubled, what would be its kinetic energy?
A: (a) K = (1/2)mv2 = .5(0.300)(15.0 m/s)2 = 33.8J
(b) K = (1/2)mv2 = .5(0.300)(30.0 m/s)2 = 135J
Q: While running, a person dissipates about 0.600 J of mechanical energy per step per
kilogram of body mass. If a 60.0 kg runner dissipates a power of 70 W during a race,
how fast is the person running? Assume a running a step is 1.5m long.
A: Concentration of energy output = (0.600 J/ kg.step)(60.0 kg)(1step/1.50m) = 24.0 J/m
F = (24.0 J/m)(1N.m/J) = 24.0 N
P = Fv  70.0W = (24.0N) v , solving for v  v = 2.92 m/s
Conversions
Length
1 meter = 3.281 ft
1 yard = .9144 meter
Mass
1kg = 2.204 lbs
Force
1N = .2248 lb
1 lb = 4.448 N
Velocity
1 m/s = 3.281 ft/s
Acceleration
1 m/s2 = 3.28 ft/s2
2 ft/s2 = .3048 m/s2
Energy
1J = .738 ft.lb
1 W = 1 J/s = 0.738 ft.lb/s
Projectile Motion
Anyone that watches a football thrown in the air has observed a projectile motion or
better known as a trajectory. The ball moves in a curved path, and its motion is simple to
analyze. The path of the football will always follow the form of a parabola if we make
two assumptions. First, that the free fall acceleration (gravity) denoted by the letter (g) is
constant over the range of the motion and it is directed downward. Second, the effect of
air resistance is neglected in order to simplify the concept. When analyzing examples of
projectile motion, it is a good habit to choose a coordinate system. For motion in two
dimensions, the preferred the coordinate system is the “X” and “Y” coordinate system.
Projectile Motion is a special case of two-dimensional motion. Examining the variables
with respect to the “X” axis, the projectile (football) experiences a constant velocity with
zero acceleration. In the “Y” axis, the football experiences a varying velocity and a
constant acceleration in the downward direction known as gravity (9.8 m/s2). The
horizontal and vertical components of our football projectile are independent of each
other, and share the common variable of time denoted as (t).
In the above figure there is two variables that represent the maximum height and range
of the projectile denoted as (h) and (R) respectively. In the game of football these two
variables are influential to the outcome of a fourth down punting play. During the fourth
down (the last play each team has) the punter generally stands behind the line of
scrimmage, catches the snap (football), and then kicks the ball. The main idea of this play
is to drive the opposing team as far back as possible before they take possession of the
ball. By exploring the above figure, a punter could easily conclude that the higher the
football is kicked the longer it will remain in action or play. In addition, he would acquire
a maximum range if he were to position the football at a 45-degree angle during the punt.
Through the relationships of variables and knowledge of concepts explained,
mathematicians have been able to increase our knowledge of earth’s laws by developing
instrumental formulas. The following formulas have been developed with the intention to
solve projectile motion related problems. Observe that other factors may occur during a
football game, which would influence the outcome of our projectile such as weather
conditions.
The height of the football is an unknown variable. This unknown variable can be found
if the initial speed (vi), the angle () in which the football is thrown, and the horizontal
distance (x) related to that point is known. The formula appears as such:

 2
g
y  (tan  i )x  
x
2
2v i cos i 

If the maximum height is desire, this unknown variable can be found if the initial speed
(vi), and the angle () in which the football is thrown are known. The formula appears as
such:
v sin 2  i
h i
2g
2


If the range is desire, this unknown variable can be found if the initial speed (vi), and
the angle () in which the football is thrown are known. The formula appears as such:
2
v i sin 2 i
R
g
The following figure shows the path of a projectile launched at an initial speed of 50 m/s
at various angles that increment by 15 degrees. Note that despite the projectile being
launched at different angles, there exist complimentary values of () that result in the
same value of R (range of the projectile).
Your team is lined up on the 5 yard line, and don't have any more downs to play. The
head coach calls you in to punt the ball (considering that you know how to punt a
football), would you punt the ball at a 15-degree angle or 60 degree angle. Why?
PITFALL PREVENTION
Acceleration at the Highest Point
Many misconceptions occur at the highest point in the path of the projectile. An
inexperienced onlooker could easily mistake the zero vertical velocity for zero vertical
acceleration. If the projectile where to experience zero acceleration at the highest point,
then the projectile would continue its path without change in velocity. In other words, the
football would keep moving into space! This is not the case in earth. We experience the
vertical acceleration known as gravity, therefore the projectile experiences gravity
(vertical acceleration) its entire path.
The Height and Range Equations
The equation provided for calculating R (range) is useful only for symmetric paths. If
the path is not symmetric, do not use this equation. A symmetric path can be defined as a
balanced path of proportions, especially in two halves of a whole.
Vector and Scalar Quantities
Some physical quantities are scalar quantities and others are vector quantities. Vectors
and scalars will be discussed in this section, in pursuit to clarify their differences. A
scalar quantity can be defined as a quantity that has magnitude, an appropriate unit of
measure, and no direction. Examples of scalar quantities are temperature, time, volume,
speed, an athlete’s weight, and even an athlete’s age. A vector quantity is completely
specified by number, appropriate units, and in addition a direction. It is imperative to
understand that a vector must be declared with a magnitude and direction; a value given
without one or the other is not a vector. Examples of a vector are an athlete’s angular
velocity, a footballs travel velocity and direction, and even wind velocity.
Adding vectors
A  Ax 2  Ay 2  11.32  4.12  12
B  Bx 2  By 2  12.52  21.7 2  25

Pitfall prevention
Generally, the inverse tangent function on calculators provides an angle between 90-degrees and +90-degree. As a consequence, if the vector you are studying lies in
the second or third quadrant, the angle measured from the positive x-axis will be the
angle your calculator returns plus 180-degrees.
R


v i 2 sin( 2 i ) 20.0 2 sin( 60 o )

 35.3m
g
9.8
t
2v i sin(  i ) 2(20.0)sin( 30 o )

 2.04s
g
9.8
v
m 15.3

 7.5 m
s
s 2.04