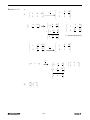Download Microsoft Word 97 - 2003 Document

Mathematics B30
Module 1
Lesson 3
Mathematics B30
Solving Systems of Equations with Matrices
109
Lesson 3
Mathematics B30
110
Lesson 3
Solving Systems of Equations with Matrices
Introduction
It is not too difficult to solve 2 equations with two unknowns or even 3 equations with 3
unknowns. Mathematics A30 demonstrated three methods: Graphical method,
Substitution method, and the Elimination method.
These methods are cumbersome when it is necessary to solve a system of more than 3
equations with more than 3 unknowns. Other methods of solving systems of equations
have been developed which enable the computer or calculator to do most of the work.
These methods make use of matrices.
The method of matrices is quicker for a system of more than two equations than the
previous methods. The graphic calculator is an excellent tool to ensure correct results.
7
y = = –1
+ 5y
x
3 –
2x
Mathematics B30
111
Lesson 3
Mathematics B30
112
Lesson 3
Objectives
After completing this lesson, you will be able to
•
determine the properties of matrices with respect to addition, scalar
multiplication, and multiplication.
•
use row operations with matrices.
•
determine the inverse of a 2 × 2 matrix.
•
solve matrix equations using multiplication by an inverse.
Mathematics B30
113
Lesson 3
Mathematics B30
114
Lesson 3
3.1 Properties of Matrices
Several properties of addition and multiplication of real numbers, that you have seen (but
perhaps not discussed), are summarized and reviewed in the following section. The
properties that have been listed will work for any real numbers. If for any case, one
correct counter example can be proven, then that is sufficient to negate the property. The
properties discussed are essential to the study of matrices in lesson two.
Six Properties of Addition and Multiplication
1.
2.
3.
4.
5.
6.
1.
Closure Properties
Commutative Properties
Associative Properties
Identity Properties
Inverse Properties
Distributive Property of Multiplication with respect to Addition
Closure Properties
If a and b are real numbers, then
a + b and ab are real numbers.
This means that the sum of two real numbers and the product of two real numbers
are real numbers themselves.
2.
Commutative Properties a  b  b  a ab  ba
The commutative property states that two real numbers may be added or multiplied
in any order without affecting the result.
Mathematics B30
115
Lesson 3
3.
a  b   c  a  b  c
ab  c  a bc 
Associative Properties
The associative properties allow us to group terms of factors in any manner we wish
without affecting the result. The operation inside the parenthesis is to be done
first.
4.
Identity Properties
•
There is a real number 0 such that a  0  a ,
or 0  a  a .
•
There is a real number 1 such that a 1  a ,
or 1  a  a .
The number 0 is called the identity element for addition and it may be added to
any real number to obtain that same real number as a sum.
The number 1 is called the identity element for multiplication and multiplying a
real number by 1 will always yield that same real number.
5.
Inverse Properties •
For each real number a, there is a single real number  a
such that
a   a   0 and  a   a  0 .
•
For each nonzero real number a, there is a single
1
real number
such that
a
1
1
a   1 and
a 1.
a
a
Each real number a has an additive inverse,  a , such that the sum is the additive
identity element 0.
1
, such that
a
their product is the multiplicative identity element 1. Note that the real number
Each nonzero real number a has multiplicative inverse, or reciprocal,
Mathematics B30
116
Lesson 3
zero, 0, does not have an inverse;
Mathematics B30
1
is not a real number, it is not defined.
0
117
Lesson 3
6.
ab  c  ab  ac
b  c a  ba  ca
Distributive Property
(Multiplication with
respect to Addition)
The distributive property allows us to change a product to a sum or a sum to a
product.
The next activity will be guided through various stages and certain steps to determine the
properties of matrices. Do the matrix operations have the same 6 properties listed above
for the real numbers? To speed up the process, keystroke patterns for certain operations
on matrices ( +,  ,  , and scalar and regular multiplication) will first be demonstrated.
For the four following keystroke patterns, enter the following matrices
in your calculator. (See lesson two for review.)
Matrix #1
Matrix #2
0
 1

A 


 8 0 .5 
Mathematics B30
 6 3

B


 7 4 
118
Lesson 3
Addition: Find A  B .
Use the following keystroke pattern.
MATRX
[A] will be displayed.
1
+
MATRX
[A] + [B] will be displayed.
2
ENTER
A   B 
This is the addition
matrix A + B.
[ [5 3 ]
[1 4 .5 ] ]
Subtraction: Find A  B .
Use the following keystroke pattern.
MATRX
[A] will be displayed.
1
MATRX
[A]
2
-
[B] will be displayed.
ENTER
[A] [B]
[ [ 7
 3]
[15  3 .5 ] ]
Mathematics B30
119
This is the subtraction
matrix A  B .
Lesson 3
Scalar Multiplication : Find 2 A .
Use the following keystroke pattern.
2
×
MATRX
2*[A] will be displayed.
1
ENTER
2 *[ A ]
This is the scalar multiplication
matrix 2 A .
[ [ 2 0 ]
[ 16 1] ]
Multiplication: Find A  B .
Use the following keystroke pattern.
MATRX
[A] will be displayed.
1
×
MATRX
[A] * [B] will be displayed.
2
ENTER
[ A ] *[ B ]
[ [ 6
 3]
[ 44 .5 26 ] ]
Mathematics B30
120
This is the multiplication matrix
AB.
Lesson 3
Mathematics B30
121
Lesson 3
Activity 3.1 - (This activity is to be sent in with Assignment #2)
Part I:
Create three 3  2 matrices.


A 









B









C







1.
Test the closure property for addition, using two of the above matrices; i.e.
check that the sum of two 3 × 2 matrices is a 3 × 2 matrix.
2.
Find A  B .
Find B  A .
What can you conclude?
What property does this illustrate?
Mathematics B30
122
Lesson 3
3.
Add  A  B   C . Add the matrices in the parenthesis first.
Add A  B  C  . Add the matrices in the parenthesis first.
Is the result the same?
What property does this illustrate?
4. Find a matrix X such that A  X  A and X  A  A ? Show the matrix X.
5. Find a matrix Y such that B + Y = Zero Matrix and Y + B = Zero Matrix? Show
the matrix Y.
Mathematics B30
123
Lesson 3
Part II: Create three 2 × 3 matrices


A 









B









C







1. Test the closure property on subtraction of matrices using two of the above
matrices. Check that the difference (subtraction) of two 2 × 3 matrices is a
2 × 3 matrix.
2. Find A  B .
Find B  A .
What can you conclude?
Mathematics B30
124
Lesson 3
Part III:


A 


Create two matrices with dimensions 2  4 and create two scalars.







B







p=
q=
1. Test the closure property for multiplication with scalars on matrices
(using pA or qB).
2. Find pqA  .
Find  pq A .
Do you obtain the same result?
What property does this illustrate?
3. Prove that  p  q A  pA  qA .
Mathematics B30
125
Lesson 3
Will p A  B   pA  pB ?
4. Is there a scalar such that when multiplied with a matrix produces the matrix
itself, that is, scalar × B = B? Show.
5. Is there a scalar such that when multiplied with a matrix produces the
opposite elements of the matrix? Show your reasoning.
6. What effect would a scalar of 0 be on a matrix?
Part IV: Create three matrices with dimensions 2  2 .

A  

Mathematics B30





B  





126

C  





Lesson 3
1. Test the closure property on matrix multiplication using two of the above
matrices.
2. Find A  B .
Find B  A .
Does A  B  B  A ?
?
Verify your conclusion by checking A  C  C  A .
.
3. Find  A  B   C .
Mathematics B30
127
Lesson 3
Find A  B  C  .
Does  A  B   C  A  B  C  ?
4. Does A B  C    A  B    A  C  ?
5. Is there a matrix T such that T  A  A and A  T  A ? If so, what is it?
6. Is there a matrix Z such that Z  B  Z and B  Z  Z ? If so, what is it?
Mathematics B30
128
Lesson 3
Based on the previous activity, fill in the blanks as to which properties are valid
for matrices and which are not. If the property is valid, write a general
statement/equation that would be true.
Summary of the Properties of Matrices
Properties of Addition of Matrices
•
•
Let A, B, C be i  j matrices.
Let O be the i  j zero matrix.
1. Closure Property
A  B is an i  j matrix.
2. Commutative Property
______________________
3. Associative Property
______________________
4. Additive-Identity Property
A O O  A  A
5. Additive-Inverse Property
______________________
Properties of Subtraction of Matrices
•
•
Let A, B, C be i  j matrices.
Let O be the i  j zero matrix.
1. Closure Property
______________________
2. Commutative Property
Does not apply.
Mathematics B30
129
Lesson 3
Properties of Scalar Multiplication of Matrices
•
•
•
Let A and B be i  j matrices.
Let O be the i  j zero matrix.
Let p and q be scalars.
1. Closure Property
______________________
2. Associative Property
pqA    pq A
3. Distributive Properties
______________________
4. Multiplicative-Identity Property
______________________
5. Multiplication Property of Negative One
______________________
6. Zero Properties
______________________
Properties of Multiplication of Matrices
•
Let A, B, and C be j  j matrices.
1. Closure Property
Only with square matrices
2. Commutative Property
______________________
3. Associative Property
______________________
4. Distributive Properties
A B  C   AB  AC
B  C A  BA  CA
5. Multiplicative-Identity Property
I j j A  A
6. Zero Property
0 j j A  0
Mathematics B30
130
Lesson 3
Mathematics B30
131
Lesson 3
3.2 Row Operations with Matrices
As seen previously, the general process used to solve a system of linear equations was to
substitute a given system by a new system that had the same solutions set, which made it
easier to solve.
For example, when finding the solution set for the linear system,
3 x  y  10
x  2 y  15
, the following
process was used.
Multiplied an
equation by a
nonzero constant
3 x  y  10 1
x  2 y  15 2
x  2 y  15 2
3 x  y  10 1
× –3
Interchanged
two equations.
Add a multiple
of one equation
to another.
x  2 y  15
 3 x  6 y  45

3 x  y  10
 5 y  35
y 7
2
x  2(7 )  15
The solution set is (1,7).
x 1
Similar skills are needed to solve matrix equations (Section 2.4). The skills are called row
operations.
Elementary Row Operations
1.
2.
3.
Mathematics B30
Interchange any row with any other row.
Multiply a row through by a non-zero constant.
Replace any row by adding a multiple of one row to another row.
132
Lesson 3
Example 1
In the matrix,
ds ettes
r
o
c
s
e C
D
R
ass C
Store A
Store B
78 135

68 144
82 

72 
would changing the order of the stores make a difference?
Rewrite this matrix showing such a change.
Solution:
ds ettes
r
o
c
s
e C
D
R
ass C
Store B
Store A
68 144

78 135
72 

82 
By changing the order of the stores, we see that there is no difference in the data. This
example supports the first statement of elementary row operations on matrices. We may
interchange any rows of matrices without there being a difference.
The second elementary row operation refers to multiplying each element of any row by a
non-zero scalar and then replacing the original row by the new row obtained by this scalar
multiplication. The new row is called a scalar multiple of the original row.
Example 2
In the matrix given below multiply the given row by a scalar that will produce the
intended result for each of the following. Begin with the original matrix in each
case.
4 1
 6


4 2
 3
 5  3 6


Mathematics B30
A)
B)
C)
D)
First row, second element to be 1.
First row, third element to be  5 .
Third row, second element to be 4.
Second row, first element to be 6.
133
Lesson 3
Write the matrix created by each operation.
Mathematics B30
134
Lesson 3
Solution:
A)
First row, second element to be 1.
4 1
 6


4 2
 3
 5  3 6


Determine the constant.
4 ?  1
?
1
4

1
4
Multiply row 1 by .
B)
4 1
6
 3 4 2 


 5  3 6 
1
4
 3
1
 2

 3
4

 5 3

1
4

2

6

First row, third element to be  5 .
4 1
 6


4 2
 3
 5  3 6


Determine the constant.
1  ?  5
?  5
Multiply row 1 by  5 .
Mathematics B30
4
 6
 3
4

 5  3
135
1
2 
6 
 5
 30  20
 3
4

 5
3
 5
2 
6 
Lesson 3
C)
4 1
 6
 3
4 2 

 5 3 6 
Third row, second element to be 4.
Determine the constant.
 3 ?  4
?
Multiply row 3 by 
D)
4
.
3
4
 6
 3
4

 5  3
1
2 
6 
4
3

 6

 3
 20
 3

4
3
4
4
4
1 
2

 8

Second row, first element to be 6.
4 1
 6


4 2
 3
 5  3 6


Determine the constant.
3?  6
?  2
Multiply row 2 by  2 .
Mathematics B30
4
 6
 3
4

 5  3
1
2 
6 
136
 2
4
1
 6
 6  8  4


 5  3
6 
Lesson 3
Example 3
For the matrix listed below complete each of the indicated row operations. Show
each result. Begin each question with the original matrix.
5
2  4


1
2
3
1
0  3


6
2 10 
A)
B)
C)
Multiply 1st row by 2, add to 3rd row.
Multiply 2nd row by  2 , add to 4th row.
Multiply 3rd row by 1, add to 2nd row.
Solution:
A)
2
Multiply 1st row by 2.
 4 5
2
Add to the 3rd row.
4
 8 10 
+ 1
0  3
5
Show the result.
B)
4
2

3
5

6
5

1 2
 8 7

2 10 
3
Multiply 2nd row by  2 .
1 2
Add to the 4th row.
Write the matrix.
Mathematics B30
A new third row.
 2
 6
+






7
8
 2  4

6
2
10 

0
0
6
2 4
3
1
0
5
1
2 
0  3

0
6
137
A new fourth row.
Lesson 3
C)

Multiply 3rd row by 1.
0  3
1
1

Add to the 2nd row.
+

Write the matrix.






0  3
1
4

3
1
2
1  1
2 4
4
1
6
5
1  1
0  3

2 10 
A new second row.
Example 3 demonstrates the third elementary row operation on matrices: adding a
common multiple of elements of one row to the corresponding elements of another row.
Exercise 3.2
ipsC
ipseC
hips
h
h
C
ed W
hit
lue R
B
1.
Player A
Player B
Player C
4
 6 10
 3 11
7 

 8
2 14 
Rewrite this matrix showing a change that demonstrates the first elementary row
operations on matrices.
 2
  10

 5

 14
2.
a.
b.
c.
d.
0
6
6
7
12 
12
28 
5
 1

 17  29 
7
In the matrix multiply the given row by a
scalar that will produce the intended result
for each of the following. Start with the
original matrix for each case. Write the
new matrix.
First row, third element to be 1.
1
Third row, first element to be .
5
Second row, fourth element to be 14.
1
Fourth row, second element to be  .
2
Mathematics B30
138
Lesson 3
3.
 2
  10

 5

 14
a.
b.
c.
d.
0
6
6
7
12 
12
28 
5
 1

 17  29 
7
In the matrix complete each of the indicated
row operations. Show each result. Begin
each question with the original matrix.
1
Multiply first row by  , add to third row.
2
1
Multiply second row by  , add to first row.
5
Multiply third row by 2, add to fourth row.
Multiply fourth row by 3, add to second row.
4.
 3 2
 5
3

4
1
In the matrix, multiply the second row by n
and add to result to the first row, such that
the third element of the first row becomes
zero.
5.
 3 4
 5
2

1
19 
In the matrix complete each of the indicated
row operations. Show each result. Begin
each question using the previous matrix
from the question above.
a.
b.
c.
d.
1
.
3
Multiply 1st row by  5 , add to 2nd row.
3
Multiply 2nd row by
.
26
4
Multiply 2nd row by , add to 1st row.
3
Multiply 1st row by
Mathematics B30
139
Lesson 3
3.3 Inverse of a 2 2 Matrix
Recall the definition of an inverse from Activity 3.1.
Inverse Properties
•
For each real number a, there is a single real number  a such that
a   a   0 and  a   a  0 .
1
•
For each nonzero real number a, there is a single real number
such
a
1
1
a 1.
that a   1 and
a
a
Each real number a has an additive inverse,  a , such that the sum is the additive
identity element 0.
1
Each nonzero real number a has a multiplicative inverse, or reciprocal, , such
a
that their product is the multiplicative identity element 1.
Additive inverse has been discussed before.
General Statements
Specific Example
Identity element 0 for addition
a  (?)  0
(?)  a  0
(?)   a
9  (?)  0
(?)   a
?  9
Therefore, a  (a)  0
?  9
Therefore, 9  (9)  0
1 2  ? ? 0 0 




3 4  ? ? 0 0 
 a b  ? ? 0 0 




 c d  ? ? 0 0 
 a  ?  0 b  ?  0  0 0 



 c  ?  0 d  ?  0  0 0 
? ?  a  b



? ?   c  d 
Mathematics B30
(?)  9  0
identity matrix for addition
? ?   1  2 



? ?  3  4 
140
Lesson 3
Let's explore multiplicative inverses on matrices further. We know:
General Statements
Specific Example
Identity element 1 for multiplication
a  ? 1
?
5  (?)  1
(?)  a  1
1
 a 1
a
?
1
 a 1
a
?
(?)  5  1
1
 5 1
5
?
1
 5 1
5
For matrices, the pattern would be the same.
original  inverse  identity 
matrix   matrix   matrix 

 
 

1 identity

A matrix
identity
A  A 1  
matrix
A
•
inverse  original  identity 
matrix   matrix   matrix 

 
 

or



identity
1
A 
A
matrix
identity
A 1  A  
matrix



6 4 
For the matrix 
 , the multiplicative inverse would be
2 5 






invers
e
6 4  ? ? 



2 5  ? ? 



identity element
for multiplication
What is the identity element for multiplication on matrices?
For multiplication, the identity element when multiplied with the original matrix,
produces the original matrix.
AI  A
Mathematics B30
IA  A
141
Lesson 3
A matrix in the form where there are 1's on the main diagonal and 0's off the main
diagonal is called an identity matrix.
1 0


0 1
•
1

0
0

0
1 0 0 


0 1 0 
0 0 1 


0 0 0

1 0 0
0 1 0

0 0 1 
When size of the identity matrix is needed, I n will be used for the n  n
identity matrix.
Example 1

 44
A 
1

 3
25
12
Verify that multiplication by the identity matrix
produces matrix A.
1
2

1

i)
ii)
I2 A  A
AI 3  A
Solution:
i)
I2 A
=
=
=
Mathematics B30
1

 1 0   44 25 2 



0 1   1 12 1
 3


1

(1  44 )   0  3  (1  25 )  (0  12 )



1

(0  44 )   1   (0  25 )  (1  12 )

 3

 44
 1

 3
25
12

 1
 1    ( 0  1) 
 2

1

 0    (1  1)
2


1
2

1

142
Lesson 3
ii)
AI 3

 44
 1

 3









=
=

 44
 1

 3
=
1
1 0 0 

2 × 0 1 0 



1
0 0 1 

25
12









(Room for
your
calculations)
1
2

1

25
12
Procedure to Determine the Inverse of a 2  2 Matrix
 a b
For A = 

c d
STEP 1 -
Find the determinant, D.
i)
Multiply ad.
ii)
Multiply bc.
Find ad  bc .
iii)
STEP 2 -
The inverse, A 1 , is:
A
Mathematics B30
D  ad  bc
1

1  d  b

D  c
a
143
Lesson 3
Example 2
6 4 
Determine the multiplicative inverse for the matrix 
 . Verify.
2 5 
Solution:
a
b 6 4 

,
 c d  2 5 
Using 
find the determinant, D.
•
•
•
The inverse,
Multiply ad.
Multiply bc.
Find ad  bc .
30
8
22
1  d  b

D  c
a
1  5  4

22  2
6
Verify the solution.
6 4  1  5  4  ?

 2 5   22   2
6  .



1 0 
0 1  (Remember: A  A 1  I )


  5 
2 4
 6 
6  22   4  22  6  22   4  22  ? 1 0 

 

  
  
0 1 
5

2

4






 6 
 2   5

2
 5   . 


  22   22 

22
22

  





30 8

22 22
10 10

22 22
Therefore,
Mathematics B30
1
22
24
22
8
22
 22
 22

0


24 
?
22  

30
  .
22 

1 0 
0 1 



0  ? 1 0 

22  . 0 1 

22 
 5  4
is the inverse for
 2
6 

144
()
6 4 
2 5  .


Lesson 3
Use the following keystroke pattern to determine the determinant of a
matrix.
Enter a matrix into the computer.
MATRIX

ENTER
[to select MATH]
[to select 1:det(]
MATRIX
Select matrix number
ENTER
Exercise 3.3
1.
Find the determinant of each of the following matrices. Show your work. Check
solutions using the calculator.
a.
4
 1
 3  6 


d.
4 3
21 


 5 2 7
b.
 44 25 
  12 20 


e.





f.
 n
n  2

5 n  3 

c.
9
2
5

3
Mathematics B30

6 

 4

145
2
7
1
2
1
 
2

14 

Lesson 3
2.
Determine the multiplicative inverse of each of the matrices in Question 1.
3.
 16
Determine the inverse of 
 24
4.
The pattern used for finding the determinant of a 3  3 matrix is as follows.
Given:
 a11
a
 21
a 31
 a 11
A  a 21
 a 31
a12
a 22
a 32
a13  a 11
a 23  a 21
a 33  a 31
 4
. Can inverses be found for all matrices?
6 
a 12
a 22
a 32
a 13 
a 23 
a 33 
a12
a 22
a 32
rewrite first t wo columns
determinant of A 33
=
–
a11 a 22 a33   a12 a 23 a31   a13 a 21 a32 
a13 a22 a31   a11 a23 a32   a12 a21 a33 
Find the determinant for the following.
a)
4  3
 1
 2
1
4 

 0  3
5 
Mathematics B30
2
3  1
1
2  3 

4
3
1
b)
146
c)
0
 1 3
 1 7
0 

 2 6  4 
Lesson 3
3.4 Solving Matrix Equations
For the system of equations
3x  y  7
2 x  5 y  1
intersection point, or solution set.
1)
, three methods are known to locate the
Graphical Method
1
3x  y  7
y  3 x  7
y
2
2 x  5 y  1
y
2
1
x
5
5
2
5
Slope =  3
Slope =
y-intercept (0, 7)
 1
y-intercept  0 , 
 5
x
Graph the two equations, given the slope and
y-intercept. From the graph observe that (2, 1) is
the solution.
2.
Substitution Method
3x  y  7
1
y  3 x  7
3
2 x  5 y  1 2
2 x  5  3 x  7   1
3 into 2
3x  y  7
2 x  15 x  35  1
3 2   y  7
17 x  34
y 1
x2
The solution is (2, 1).
Mathematics B30
147
Lesson 3
3.
Elimination Method
3x  y  7
1
2 x  5 y  1
2
×5
15 x  5 y  35
 2 x  5 y  1
17x
= 34
= 2
x
3 2   y  7
y 1
The solution is (2, 1).
There are two other methods that can be used to locate the intersection point of systems of
equations. Both of the new methods use matrices.
Matrix Method I - Row Operations
A matrix can be constructed based on the coefficients and constant terms.
constant terms
3x 
y 7
2 x  5 y  1
1
2
1
7
3
2  5  1 


Coefficients Coefficients
for the x’s
for the y’s
The matrix formed is called an augmented matrix where the last column consists of the
constant terms, and the beginning columns consist of the coefficients of each variable.
When constructing augmented matrices, the unknowns must be written in
the same order in each equation. If a variable is missing, a 0 (zero) must be
used as a place holder.
For the system of equations
ax  by  m
cx  dy  n
, when solving using the
a
method of row operations, create a matrix 
 c
Mathematics B30
148
b m
.
d n 
Lesson 3
To solve an augmented matrix the elementary row operations are used so that the
identity matrix is produced on the left and the numbers that are remaining in the
last column will be the solution.
Elementary Row Operations
1.
2.
3.
Interchange any row with another row.
Multiply a row by a non-zero constant.
Replace any row by adding a multiple of one row to another row.
Suggested Strategy (for a 2 × 2 matrix)
Step 1
The entry in the first row, first column to be a 1.
Step 2
All other entries in the first column to be 0.
Step 3
The entry in the second row, second column to be a 1.
Step 4
All other entries in the second column to be 0.
Step 5
Check: Is the identity matrix on the left hand side of the
augmented matrix?
Example 1
Solve the system of equations using the method of row operations.
3x  y  7
2 x  5 y  1
Mathematics B30
149
Lesson 3
Solution:
3x  y  7


2 x  5 y  1
Step 1
First row, first column

1
 3
 2 5

7
 1
1
3
1

 1
3

 2 5

7
3

 1

Step 2
 1
1 3

 2

 2
7
3 

+ 




14 
3 
15
3
3
 
3
17

3
17 
 
3 
2 
0
2
3





1
3
17
0 
3
1
7
3
17 
 
3
All other entries in
column 1 are zero.
Step 3





1
3
17
0 
3
1
7
3
17 
 
3


1

0

3
17
7
3

1 1

1
3
second column, second row
Mathematics B30
150
Lesson 3
Step 4
0
1 1

1
3
All other entries
zeros
1 0 2 


0 1 1 
1

 0 3

1

  1
3


 1

1
 
3
7
3 
0
6
3 
Step 5
1 0 2 
0 1 1


1 0 
0 1 


1x  0 y  2
x2
0x 1y  1
y 1
 2, 1
Identity matrix ()
Matrix Method II - Inverses
For the system of equations
ax  by  m
cx  dy  n
inverses, create following the matrices.
, when solving using the method of
 a b   x  m 
 c d    y   n 

    
Mathematics B30
151
Lesson 3
When solving simple equations like 6  s  42 , the math used was:
1
1
   6 s     42
6
6
inverse
inverse
6 6 s  6 42
1
1
s 7
Similarly, if we left-multiply both sides of the equation by the inverse matrix the solution
can be found.
Multiplication of matrices is not necessarily commutative. A  B   B  A 
 a b   x  m 
 c d    y   n 

    
1  d  b  a b   x  1  d  b  m 




a   c d   y  D   c
a   n 
D   c
* left multiply
the matrices
produces the identity matrix
1 0   x 
0 1    y  

  
x
 y 
 
Mathematics B30
152
1  d  b  m 

a   n 
D   c
1  d  b  m 

a   n 
D   c
Lesson 3
Example 2
Solve using the method of inverse.
3x  y  7
2 x  5 y  1
Solution:
1  x   7 
 3
 2  5    y    1 

    
1
 3
1
The inverse of 
is

 17
 2  5
5
17
2

17
 5
 2

 1
.
3 
1 
17   3 1    x    1   5  1   7 
 3  2  5   y  17  2 3   1 

17 
 15 2
 17  17
 6 6
 
17 17
5 5
5

x




17 17
 17



2 15  y 
2



17 17 
17
1 
17   7 
 3   1 

17 
 35 1 
1 0   x   17  17 
0 1   y   14 3 

    
 17 17 
 x  2 
 y   1 
   
Mathematics B30
153
 2, 1 is the solution.
Lesson 3
Use the following keystroke pattern to solve the system of equations
using the method of inverses.
Enter matrix A and matrix B.
1
 3
A 

 2  5
System of Equations
 7
B 
 1 
3x  y  7
2 x  5 y  1
At home screen [2nd MODE]...
MATRX
ENTER
[to select matrix A]
x 1
MATRX
2
[A]-1 [B] will be displayed
ENTER
[ [2]
[1] ]
Exercise 3.4
1.
Solve the system of equations by using the
i)
ii)
method of row operations,
method of inverses.
Check your solution on the calculator.
a.
b.
c.
3 a  4 b  10
2 a  5b  1
4x 5y  8
6 x  4 y  11
x 2y 7
3 x  y  14
Mathematics B30
154
Lesson 3
d.
e.
f.
2.
10 s  t  24
 s  3 t  15
3x  y   2 x  7
Hint: Put in the form
5x  y   6  1  2 y  2 x 
ax  by  m
cx  dy  n
29
4
6x  4 y  8
4x 5y 
Create the augmented matrix and then use the graphing calculator to solve the
given system of equations. [If a graphing calculator is not available, produce the
1 0 0 
identity matrix 0 1 0  on the left hand side of the matrix. (Method: row
0 0 1 
operations)].
4x  y  z  5
a.
3 x  3 y  2 z  22
x 2y  z  3
x  2 y  5z  4
b.
2 x  y  2 z  4
6x 3y  4z  6
c.
x  2 z  6
y  3z  9
2x  z  3
3.
A manager of a double movie theatre is preparing her day’s admissions. However,
the till had a malfunction and did not register all the information. She knows the
total receipts from Theatre 1 are $905, and that there were 62 adults and 84
children in attendance. Theatre 2’s proceeds are $1203, with 114 adults and 52
children. She needs to determine the admission charged adults and children on
that day. She thinks for a moment and then proceeds to find the solution. Recreate her solution by writing equations to represent the given data and solve by
Mathematics B30
155
Lesson 3
using matrices.
Mathematics B30
156
Lesson 3
Self Evaluation
1.
In the matrix multiply the given row by a scalar that will produce the intended
result. Start with the original matrix for each question.
2 6
 1
 4  4 3


 7 12 8 
2.
c.
a.
b.
Multiply 1st row by  3 , addto 2nd row.
1
Multiply 2nd row by  , add to 3rd row.
2
Find the determinant of each matrix.
a.
4.
b.
First row, third element to be 2.
1
Second row, first element to be .
8
Third row, second element to be 1.
In the matrix, complete the indicated row operations. Start with the original
matrix for each question.
2  3 2 
6 2
1 

4 1  7 
3.
a.
5 0 
6 3 


 3  14 
21
16 

b.
Solve the system of equations by using the
i)
method of row operations.
ii)
method of inverses.
Show your work.
a.
5x  3 y  2
b.
4x 3y  2
Mathematics B30
6 a  2b  1
4 a  3b 
157
17
6
Lesson 3
Summary – Lesson 3
•
Create a summary of this lesson to assist you come examination time.
•
Each summary is to be sent in with the assignment to be evaluated.
•
Items to include in a summary:
•
definitions
•
formulas
•
calculator “shortcuts”
Mathematics B30
158
Lesson 3
Mathematics B30
159
Lesson 3
Answers to Exercises
Exercise 3.1
Activity (to be handed in)
Exercise 3.2
1.
Answers will vary. One possible solution is:

2.a)
b)
c)
Mathematics B30
 2

  10
 5

 14
0
 2

  10
 5

 14
0
 2

  10
 5

 14
0
6
6
7
6
6
7
6
6
7
7
12 

12
28 
5
 1

 17  29 
7
12 

12
28 
5
 1

 17  29 
1
7
12 

12
28 
5
 1

 17  29 
7
160

1
25

1
2
 2
 7

  10

 5

 14
0
6
6
7
12 
7 

12
28 

5
 1

 17  29 
0
 2

6
  10

 1
6


25
 5
 14
7






2 0
1
7
12
1
5
 17
12 

28 

1 

25 
 29 
12 

5 3
6
14 
5 6
5
 1

14 7  17  29 
7
Lesson 3
 2

  10
 5

 14
d)
12 

12
28 
5
 1

 17  29 
0
0
 2

6
  10
 5
6


1
 1


2
7
6
6
7

1
14
12 

28 
 1


29 
14 
7
12
5
17
14
Answer:
3.a)
b)
 2

  10
 5

 14
 10
10
6
6
7
6 12 28 
12 

12
28 
5
 1

 17  29 
7

1

2





1
5
 5
Mathematics B30
6  5  1
6

  4
7

 6
2

5
 1

 7

17
6 
2
1
6

2


5

  2
0
5

 0
c)

0
2
 10
 14
 4
161

12

5
7
28 
 
5 
12 
6
5
23
5
32 
5 
12
 10
 2
7  17
 29 
 27
 31 
19
 2

  10

 4


 14

 0

  10

 5


 14

0
7
6
12
6

7
 17

 2 0

6
  10
 5 6

4 19

6
5
6
6
7
12 

28 

 7


 29 
17
2
32 
5 

12
28 

5
 1


 17  29 

23
5
12 

12
28 
5
 1

 27  31 
7
Lesson 3
d)
3
14 7  17  29

 42
  10
 32
21  51  87 
6
12
28 
27
 39
 59 






2
0
32
27
5
6
14
7
12 

 39  59 
5
 1

 17  29 
7
Goal: Become Zero
4.
 3  2 4


3 1
 5
 4

20
3
23

5.
a.
 3 4
 5
2

b.
4

 1 3

 5
2

1
19 
1
3

19 

1
3
 12
 23  14

3
 5
 4
2
4
 14
0
4

1


3

 5
2

4

1  3
1
3

19 

1
3 
4

 1 3

26
 0
3

Mathematics B30
162
0
1
 5

 5

 5
20
3
2
5
3 
19 

 0
26
3
52 
3 
1
3
52 

3 
Lesson 3
c)
d)
4

 1 3

26
 0
3


0
1
1
3
52 

3 
2


 1

 0

3
26

1.
a.
b.
c.
d.
e.
f.
2.
Mathematics B30
1
3

2

1
4

0
4
3
8
3 

 1

4
3
1
3 
3
1
Exercise 3.3
4
3
0
1 0 3 


0 1 2 
3
6
 580
 28
13 21
1
4
4
2
n 6
a.
1  6  4 
1
6  3
b.
1  20
 580  12
c.

1 4

 28  5
 3
 25 
 44 

 6
9

2
163
Lesson 3
3.
d.
 2 7  21 
21  2 7  21 




5
4 3  273 
5
4 3
13 21 
e.

4  14

17   1
 2
f.
n
1 n  3
  5 n  2
n 6 

1
1
2
2

7
2
 16 6    4 24   96   96   0
Inverse 
1 6
0  24
4
 16 
Division by zero is undefined,
therefore, the inverse cannot be
determined. We can conclude that
not all matrices have inverses.
4.
Mathematics B30
a.
b.
c.
39
36
 40
164
Lesson 3
Exercise 3.4 1.
a.
i)



 10 
5
1
2
4

1  3

4
3

10 
3 





1
3

 2

 2
8
3






4
3
23
3

1
0
0
1
1

10 
3
23 

3 


23
3
2
23
10 
3

1

1
0
4
3
23
3


10 
3
23 

3 
( means therefore)

1
4
3
0
1

10 
3

1

4
3

0


1

Mathematics B30





23 
3 
4
3 
4
3
4

 1 
3

ii)

5
3
3 





3
4
3
20 
3 
15

  2
3


 0


1
0

 1

 0
0  2
1
1
10 
3 
6
 
3
a    2 
b    1
   
165
Lesson 3
b.
i)

5
 4
 6 4


 1

 1

 0

5
4
1






2
4 

46 

 0
1
0
5
4
 46
4
1
5

 1
4

 6 4

4
8
11 

2

5
4
1
 6
30


6


4

16

  6 
4


 12 

 46
4

 1





2

 1

4 
46 

0
Mathematics B30

11 






1
0
5
4
 46
4

2

 1

4
46

5
5

0  4

5

 1
4

4

1


 1

 0


2

11 

0
1
0
5
46 
92 
46 
87 
46 
87 
46 
2 

23 
166
Lesson 3
ii)
5  x   8 
 4
 6  4    y   11 

    
5
 4
1  4
The inverse of 



 6  4   46   6
 16  30
 5
4 
 46
1
 46
 4
 6


 5 4
5 x  

4   6  4   y  

4
5 
46 46   8 
6  4  11 

46 46 
5
4

1 0   x   46 8   46 11 

0 1   y    6

    8   4 11 
46
 46

 87 
 x   46 
 y   2 
   
 23 
c)
i)
Mathematics B30
 1
 0

0  3
1  5 
167
Lesson 3
ii)
 1  2  x   7


 3
1  y   14 

 1  2
1 1
The inverse of 
is 

1
7  3
 3
 1
2 1  2 x   7

1   3
1  y    3
 7
1 1
7  3
2
.
1 
2
7  7
1   14 

7
 1 2

7      14 

1 0   x 
7  7 

0 1   y      3 
1

  
7   14 
  7  7

 x   3 
 y    5 
   
d)

i)
 1  24 
3  15 
 10
 1


 1

1
10

24 
10 
1

1


 1

10

Mathematics B30
1
0

1
10
29
10
1

 1  10

30

  1
10

1
24 
10 
174 


10 

168


3

 0






24 
10 

 15 

1
10
10
29






29
10
1
0

24 
10 

150 
10 

174 
10 
1
10
1

24 
10 

 6

Lesson 3

0
1

 6
1
10

0

1
10
1

 1 
10


1

 1

 0
ii.
 3
1  6 
0
 24 
10 
 30 
10 
s  3, t  6
s   3 
 t    6 
   
e)
i)
0
6
10 
3x  y   2 x  7
3x  3 y  2x 7
x 3y 7
5  x  y   6  1 
2 y  2 x 
5x  5 y  6  1  2 y  4x
x 3y 7
1 0 7 
0 1 0 



Mathematics B30
169
Lesson 3
ii)
 1  3   x  7 


 1
3   y  7 

 1  3
1 3
The inverse of 
is 

3
6  1
 1
 3
3 1  3 x   6

1   1
3   y    1
 6
1 3
6  1
3
.
1
3
6  7 
1  7 

6
  3   3 
7
7
1
0
x

     6   6 

0 1   y    1

    7   1 7 
6 
 6
 x  7 
 y   0 
   
f)
i)
1

5
 4

 6 4

29   4
4 

8


 1
29 
 6
16 
5
4
5

 1
4

 6 4

30


6


4

16

  6 
4


 0

Mathematics B30
170
29 
16 

8


46
4

174 
16 
128 
16 

46 
16 
Lesson 3






 0
1
0
1
5
4
 46
4
29 
16 
 46 

16 
1
4 


46
5
4
5

0


4

5

 1
4


1

ii)
Mathematics B30

 1

 0

4
0
5 
 
16 
29 
16 
29 
16 
1

1
4
5
4

1

0

0
1
3
2
1

4
24 
16 
3 
x
  2
 y   1 
   
4 
171
Lesson 3

2)

1
1
4
a)
5
4 
1
4
1
1
 4
 3
3 2

 1  2  1

 0


1
1
4
1
4
5
4 
 1
9
4

3
4

8
4

9

 0 4


0
9
4

11
4
11

0 1  9
Mathematics B30

73 
4 
73 
9 







9

1
0
0








15 
4 
88 
4 
73 
4 
11
4
1

 1  4

8

  1 
4

4
1
1

 1
4
4

 3
3 2

 1  2 1

4
5
22 
3 
3

 3  4

12

  3
4

 3
1

4
4
5
 
4
12 
4 

5
4
7
4 
1
4

1
4
1
4
11
1 
9
9
5


4
4







1
0
1
1
0
0
5
4

22 

3

5
4
73 

4 
3

1
1
4
4
9
11

4
4
2
1
1
4
9
4
9

4
5
4
73 

4 
7
4 
1
4
11

4
5

4
5
4
73 

9 
7
4 
1
4

0

1
4
11
36

 1

1
4
9
36

1

0
20
36
172


73 
36 
45 
36 

28 
36 
20

0
1
36

11
0
1 
9

9
5
0 


4
4

28 
36 
73 

9 
7
4 
Lesson 3

11

0 1  9
9
4
73 
9 

0

9
4
9

 0 
4








1
0
0
1
0
0
20
36
11

9
4

28 
36 
73 

9  1
4
20 



0
0
1
0
0
1
0
0
20
36
11

9
1

0 0

11
9

0 1

0
0 1  5

55 
9 
73 
9 
18 
9 
0
5
4
7
4 
16
4
80 
4 


0

0 







1
0
20
36
0
1
0
0
0
1

28 
36 

2

 5

 20
36
20

0 0  36

20

 1 0
36


1 0

 1
 0

 0
Mathematics B30
73 
4 
28 
36 
73 

9 
 5


11

 0 1 
9


11
4
11
9
1  5








173
100 
36 

72 
36 
0
0
1
0
28 
36 
2
0
2 
1  5 
0
Lesson 3
Questions with 3 equations with three variables, 4 equations with 4
variables, etc. can be solved quicker using technology.
1
1
 5
 4


Enter matrices A  3
3  2  and B  22  on the calculator

 3 
 1  2  1
x
A   y   B
 z 
1
1  x   5 
 4
 3
3  2    y   22 

 1  2  1   z   3 
x
1
A  A   y   A 1  B
 z 
x
 y   A 1 B 
 
 z 
 x   2
 y   2
   
 z   5 
 
b.
* using the theory of
inverses with the
graphing calculator.
 x   5
 y    8 
   
 z   3 
Mathematics B30
174
Lesson 3
c.
x  4
 y    6 
   
 z   5 
x  0 y  2 z  6
0x  y  3z  9
2x  0 y  z  3
Forms the matrix
3.
 1

 0

 2
 2  6

1
3
9

0 1
3 
0
Let a represent the cost of adult tickets.
Let c represent the cost of childrens tickets.
62 a  84 c  905
114 a  52 c  1203
i)
 62
 114

ii)
 62
114

905 
The matrix used for the method row operations.
52 1203 
84
84   x   905 
The matrices used for the method of inverses.


52   y  1203 
The cost of adult tickets is $8.50.
The cost of childrens tickets is $4.50.
Mathematics B30
175
Lesson 3
Answers to Self Evaluation

1.
2.
a.
2
 1


 4 4

  7 12
6


3

8 
b.
2
 1

1
 1
 8 8

  7 12
6

3 
32 

8 
c.
 1


 4

 7
 12
a.

Mathematics B30
2 3
2
4
1
2
×3
1
3
 1
 3

 4


 7

2
3
4
12

2

3


8

1
8
1 1
? 
8 4
1
?
32
4? 
6


3

2
3 
 6
  6
 0
176
9
 6
2
1
11
 5
 2


 0

 4
3
2


11  5 

1  7 
Lesson 3
b.
6
2 1

1
2
3.
a.
b.
15
316    14 21   342
4.
a.
4, 6 
b.
1 1
 , 
3 2
Mathematics B30

 3

1

 4

1

 1

0
177
1 
2 
14 
 
2








2
3
6
2
1
0
2 
1
15 
 
2
15 
2 
Lesson 3