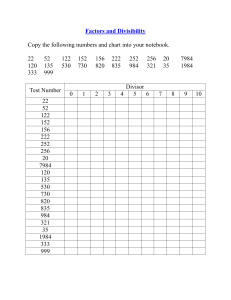
divisibility rules - Biblical Christian World View
... We have not summed the digits for a reason. The first observation to make is that 100 is a multiple of 4. This means that 200, 300, 400 and all multiples of 100 are also multiples of 4. This is an important observation because when we consider a number like 458,248, we know that 400,000 is divisible ...
... We have not summed the digits for a reason. The first observation to make is that 100 is a multiple of 4. This means that 200, 300, 400 and all multiples of 100 are also multiples of 4. This is an important observation because when we consider a number like 458,248, we know that 400,000 is divisible ...
Advanced Problems and Solutions
... Sums of reciprocals of primes with complex exponents, 7.1(1969)56 Shades of Euler, 8.4(1970)390 Triple sums of Fibonacci squares, 7.1(1969)57 Triple Threat, 8.4(1970)391 Some two variable generating functions, 7.1(1969)57 Sum Inversion, 8.5(1970)488 Complete sequence of Fibonacci powers, 7.1(1969)58 ...
... Sums of reciprocals of primes with complex exponents, 7.1(1969)56 Shades of Euler, 8.4(1970)390 Triple sums of Fibonacci squares, 7.1(1969)57 Triple Threat, 8.4(1970)391 Some two variable generating functions, 7.1(1969)57 Sum Inversion, 8.5(1970)488 Complete sequence of Fibonacci powers, 7.1(1969)58 ...
On the works of Euler and his followers on spherical geometry
... poorly known, except for some quotes in the work of Ptolemy. Chasles, in his Aperçu historique [5] (1837), after mentioning the early works on spherical geometry by Theodosius, Menelaus and Ptolemy, adds the following (p. 236): “This doctrine [of spherical lines and spherical triangles], which is a ...
... poorly known, except for some quotes in the work of Ptolemy. Chasles, in his Aperçu historique [5] (1837), after mentioning the early works on spherical geometry by Theodosius, Menelaus and Ptolemy, adds the following (p. 236): “This doctrine [of spherical lines and spherical triangles], which is a ...
Projecto Delfos - Departamento de Matemática
... a cos2 x + b cos x + c = 0 . Using the numbers a, b, c, form a quadratic equation in cos 2x, whose roots are the same as those of the original equation. Compare the equations in cos x and cos 2x for a = 4, b = 2, c = −1 . 1959/4: Construct a right triangle with given hypotenuse c such that the media ...
... a cos2 x + b cos x + c = 0 . Using the numbers a, b, c, form a quadratic equation in cos 2x, whose roots are the same as those of the original equation. Compare the equations in cos x and cos 2x for a = 4, b = 2, c = −1 . 1959/4: Construct a right triangle with given hypotenuse c such that the media ...
Course-504 Learning Mathematics at Elementary Level
... In these systems of numbers, it was difficult to remember the numerals for different numbers. Further, it was difficult at the time of working out various operations like addition, subtraction etc. India’s Contribution: The present decimal system i.e. the numbers based on ten digits i.e.,0, 1, 2, 3, ...
... In these systems of numbers, it was difficult to remember the numerals for different numbers. Further, it was difficult at the time of working out various operations like addition, subtraction etc. India’s Contribution: The present decimal system i.e. the numbers based on ten digits i.e.,0, 1, 2, 3, ...
Class VI Chapter 3 – Playing with Numbers Maths Exercise 3.1
... (a) The sum of three odd numbers is even. (b) The sum of two odd numbers and one even number is even. (c) The product of three odd numbers is odd. (d) If an even number is divided by 2, the quotient is always odd. (e) All prime numbers are odd. (f) Prime numbers do not have any factors. (g) Sum of t ...
... (a) The sum of three odd numbers is even. (b) The sum of two odd numbers and one even number is even. (c) The product of three odd numbers is odd. (d) If an even number is divided by 2, the quotient is always odd. (e) All prime numbers are odd. (f) Prime numbers do not have any factors. (g) Sum of t ...
List of Olymon problems 1-300 - Department of Mathematics
... The word unique means exactly one. A regular octahedron is a solid figure with eight faces, each of which is an equilateral triangle. You can think of gluing two square pyramids together along the square bases. The symbol buc denotes the greatest integer that does not exceed u. An acute triangle has ...
... The word unique means exactly one. A regular octahedron is a solid figure with eight faces, each of which is an equilateral triangle. You can think of gluing two square pyramids together along the square bases. The symbol buc denotes the greatest integer that does not exceed u. An acute triangle has ...
Fibonacci numbers
... A Fibonacci prime is a Fibonacci number that is prime. The first few are: 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, … (sequence A005478 in OEIS). Fibonacci primes with thousands of digits have been found, but it is not known whether there are infinitely many.[29] Fkn is divisible by Fn, so, apart f ...
... A Fibonacci prime is a Fibonacci number that is prime. The first few are: 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, … (sequence A005478 in OEIS). Fibonacci primes with thousands of digits have been found, but it is not known whether there are infinitely many.[29] Fkn is divisible by Fn, so, apart f ...
Divisibility - Dalton State
... • Double the ones digit and subtract from the remaining digits • If that number is equal to zero or divisible by 7, then the original number is • If your number is still a big number, repeat the process ...
... • Double the ones digit and subtract from the remaining digits • If that number is equal to zero or divisible by 7, then the original number is • If your number is still a big number, repeat the process ...
Criterions for divisibility
... • If Kathy wrote down three numbers, then one can choose either two even numbers, or two odd ones, from written numbers. The sum of the chosen numbers will be even. ...
... • If Kathy wrote down three numbers, then one can choose either two even numbers, or two odd ones, from written numbers. The sum of the chosen numbers will be even. ...
List of Olymon problems 301-600
... 372. Let bn be the number of integers whose digits are all 1, 3, 4 and whose digits sum to n. Prove that bn is a perfect square when n is even. 373. For each positive integer n, define an = 1 + 22 + 33 + · · · + nn . Prove that there are infinitely many values of n for which an is an odd composite n ...
... 372. Let bn be the number of integers whose digits are all 1, 3, 4 and whose digits sum to n. Prove that bn is a perfect square when n is even. 373. For each positive integer n, define an = 1 + 22 + 33 + · · · + nn . Prove that there are infinitely many values of n for which an is an odd composite n ...