* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download KEY - Rose
Crossbar switch wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Magnetic core wikipedia , lookup
Power MOSFET wikipedia , lookup
Operational amplifier wikipedia , lookup
Two-port network wikipedia , lookup
Wilson current mirror wikipedia , lookup
Galvanometer wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
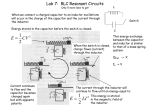
RLC circuit wikipedia , lookup
Current source wikipedia , lookup
Electrical ballast wikipedia , lookup
Rectiverter wikipedia , lookup
Physics III Homework IV CJ Chapter 33; 60, 72, 73, 74 and Chapter 23; 4, 9, 14, 16 33.60. Model: Assume the magnetic field is uniform over the loop. Visualize: The motion of the eye will change the orientation of the loop relative to the fixed field direction resulting in an induced emf. Solve: We are just interested in the emf due to the motion of the eye so we can ignore the details of the time dependence of the change. From Faraday’s law, E coil N N r 2 B cos f cos i d cos N NAB dt t t t 20 3 10 3 m 1.0 T cos85 cos90 2 0.20 s 2.46 10 4 V Assess: This is a reasonable emf to measure, although you might need some amplification. 33.72. Model: Assume negligible resistance in the circuit. Visualize: Energy is conserved. The maximum voltage on the right capacitor will occur when all of the energy from the left capacitor is transferred to the right one. Solve: (a) The voltage is calculated as follows: 1 2 2 C1VC12 21 C2 VC2 VC2 C1 300 VC1 100 V 50 V C2 1200 (b) Closing S1 causes the charge and current of the left LC circuit to oscillate with period TL. After one-quarter of a period, the 300 F capacitor is completely discharged and the current through the inductor is maximum. At that instant we’ll open S1 and close S2. Then the right LC circuit will start to oscillate with period TR and the inductor current will charge the 1200 F capacitor. The capacitor will be fully charged after one-quarter of a period, so we will open S2 at that time to keep the charge on the 1200 F capacitor. The periods are 2 2 LC1 2 (5.3 H)(300 10 6 F) 0.25 s 14 TL 0.0625 s L 2 TR 2 LC2 2 (5.3 H)(1200 10 6 F) 0.50 s 14 TR 0.1250 s R TL So the procedure is to close S1 at t 0 s, open S1 and close S2 at t 0.0625 s, then open S2 at t 0/1250 s. 33.73. Model: Assume an ideal inductor and an ideal (resistanceless) battery. Visualize: Please refer to figure P33.73. The current through the battery is the sum of the currents through the left and right branches of the circuit. Solve: (a) Because the switch has been open a long time, no current is flowing the instant before the switch is closed. A basic property of an ideal inductor is that the current through it cannot change instantaneously. This is because the potential difference VL –L(dI/dt) would become infinite for an instantaneous change of current, and that is not physically possible. Because the current through the inductor was zero before the switch was closed, it must still be zero (or very close to it) immediately after the switch is closed. Conservation of current requires the current through the entire right branch to be the same as that through the inductor, so it is also zero immediately after the switch is closed. The only current is through the left 10 resistor, which sees the full battery potential of the battery. Thus Ibat Ileft Vbat/R (10 V)/(10 ) 1.0 A. (b) The current through the inductor increases as time passes. Once the current Iright reaches a steady value and is no longer changing, the potential difference across the inductor is VL –L(dI/dt) 0 V. An ideal inductor has no resistance, so the inductor simply acts like a wire and has no effect on the circuit. The circuit is that of two 10 resistors in parallel. The equivalent resistance is 5 and the battery current is Ibat (10 V)/(5 ) 2.0 A. 33.74. Model: Assume an ideal inductor and an ideal (resistanceless) battery. Visualize: Please refer to figure P33.74. Solve: (a) Because the switch has been open a long time, no current is flowing the instant before the switch is closed. A basic property of an ideal inductor is that the current through it cannot change instantaneously. This is because the potential difference VL –L(dI/dt) would become infinite for an instantaneous change of current, and that is not physically possible. Because the current through the inductor was zero before the switch was closed, it must still be zero (or very close to it) immediately after the switch is closed. Consequently, the inductor has no effect on the circuit. It is simply a 10 resistor and 20 resistor in series with the battery. The equivalent resistance is 30 , so the current through the circuit (including through the 20 resistor) is I Vbat/Req (30 V)/(30 ) 1.0 A. (b) After a long time, the currents in the circuit will reach steady values and no longer change. With steady currents, the potential difference across the inductor is VL – L(dI/dt) 0 V. An ideal inductor has no resistance (R 0 ), so the inductor simply acts like a wire. In this case, the inductor “shorts out” the 20 resistor. All current from the 10 resistor flows through the resistanceless inductor, so the current through the 20 resistor is 0 A. (c) When the switch has been closed a long time, and the inductor is shorting out the 20 resistor, the current passing through the 10 resistor and through the inductor is I (30 V)/(10 ) 3.0 A. Because the current through an inductor cannot change instantaneously, the current must remain 3.0 A immediately after the switch reopens. This current must go somewhere (conservation of current), but now the open switch prevents the current from going back to the battery. Instead, it must flow upward through the 20 resistor. That is, the current flows around the LR circuit consisting of the 20 resistor and the inductor. This current will decay with time, with time constant L/R, but immediately after the switch reopens the current is 3.0 A. 23.4. Model: sources. Light rays travel in straight lines. Also, the red and green light bulbs are point Visualize : Solve: The width of the aperture is w 1 m. From the geometry of the figure for red light, w2 x x 2w 2 1.0 m 2.0 m 1m 3m 1m The red light illuminates the wall from x = 0.50 m to x = 4.50 m. For the green light, x1 w4 x1 1.0 m 1m 3m 1m x2 3w 4 x2 3.0 m 1m 3m 1m Because the back wall exists only for 2.75 m to the left of the green light source, the green light has a range from x 0 m to x 3.75 m. 23.9. Model: Light rays travel in straight lines and follow the law of reflection. Visualize : To determine the angle , we must know the point P on the mirror where the ray is incident. P is a distance x2 from the far wall and a horizontal distance x1 from the laser source. The ray from the source must strike P so that the angle of incidence i is equal to the angle of reflection r. Solve: From the geometry of the diagram, tan 1.5 m 3 m x2 x1 1.5 m 3m 10 1.5 m x1 15 m 2 3 m x1 x1 m 5 m x1 x1 3 tan 23.14. Model: x1 x2 5 m 3m 9 0.90 42 x1 10 Use the ray model of light. The sun is a point source of light. Visualize : A ray that arrives at the diver 50 above horizontal refracted into the water at water 40. Solve: Using Snell’s law at the water-air boundary nair sinair nwater sin water sin air air nwater 1.33 sin water sin40 nair 1.0 58.7 Thus the height above the horizon is = 90 air = 31.3. Because the sun is far away from the fisherman (and the diver), the fisherman will see the sun at the same angle of 31.3 above the horizon. 23.16. Model: Use the ray model of light. For an angle of incidence greater than the critical angle, the ray of light undergoes total internal reflection. Visualize : Solve: The critical angle of incidence is given by Equation 23.9: ncladding 1 1.48 sin 67.7 n 1.60 core c sin 1 Thus, the maximum angle a light ray can make with the wall of the core to remain inside the fiber is 90 67.7 22.3. Assess: We can have total internal reflection because ncore ncladding.