Download WRL0001.tmp

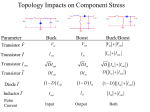
6/27/2017
493695446
1/27
Amplifier Gain
One interesting characteristic of an amplifier is that it is a unilateral device—it
makes a big difference which end you use as the input!
Most passive linear circuits (e.g., using only R, L and C) are reciprocal. With
respect to a 2-port device, reciprocity means:
Z 12   Z 21 
and
Y12    Y21  
For example, consider these two open-circuit voltage measurements:
I1

V1

2-port
Circuit

V2  Z 21I1

I2

V1  Z 12I2

Jim Stiles
The Univ. of Kansas
2-port
Circuit

V2

Dept. of EECS
6/27/2017
493695446
2/27
Every function an Eigen function
If this linear two-port circuit is also reciprocal, then when the two currents I1
and I 2 are equal, so too will be the resulting open-circuit voltages V1 and V2 !
Thus, a reciprocal 2-port circuit will have the property:
V1 V2
when
I1  I 2
Note this would likewise mean that:
V2 V1

I1 I 2
And since (because of the open-circuits!):
V2  Z 21I1
and
V1  Z 12I2
We can conclude from this “experiment” that these trans-impedance
parameters of a reciprocal 2-port device are equal:
Z 12   Z 21 
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
3/27
Every function an Eigen function
Contrast this with an amplifier.
A current on the input port will indeed produce a voltage on an open-circuited
output:
I1


V1
V2  Z 21I1


However, amplifiers are not reciprocal. Placing the same current at the output
will not create the equal voltage on the input—in fact, it will produce no voltage
at all!
I
2


V1  0
V2

Jim Stiles

The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
4/27
Every function an Eigen function
Since for this open-circuited input port we know that:
Z 12 
V1
,
I2
the fact that voltage produced at the input port is zero (V1  0 ) means the
trans-impedance parameter Z 12 is likewise zero (or nearly so) for unilateral
amplifiers:
Z 12ω   0
(for amplifiers)
Thus, the two equations describing an amplifier (a two-port device) simplify
nicely.
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
5/27
Every function an Eigen function
Beginning with:
V1  Z11 I1  Z12 I2
V2  Z 21 I1  Z 22 I2
Now since Z 12  0 , we find:
V1  Z11 I1
V2  Z 21 I1  Z 22 I2
Q: Gee; I’m sort of unimpressed by this simplification—I was hoping the result
would be a little more—simple.
A: Actually, the two equations above represent a tremendous simplification—it
completely decouples the input port from the output, and it allows us to assign
very real physical interpretations to the remaining impedance parameters!
To see all these benefits (try to remain calm), we will now make a few changes in
the notation.
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
6/27
Every function an Eigen function
First we explicitly denote voltage V1 as Vin , and likewise V2 as Vout (the same with
currents I).
Additionally, we change the current definition at the output port, reversing the
direction of positive current as flowing outward from the output port. Thus:
Iout  I2
And so, a tidy summary:
Iin
Iout


Vin
Vout


Vin  Z 11 Iin
Vout  Z 21 Iin  Z 22 Iout
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
7/27
Every function an Eigen function
From this summary, it is evident that the relationship between the input current
and input voltage is determined by impedance parameter Z11 —and Z11 only:
Z11 
Vin
Iin
Thus, the impedance parameter Z11 is known as the input impedance Z in of an
(unilateral!) amplifier:
Zin ω 
Jim Stiles
Vin ω 
Iin ω 
 Z11ω 
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
8/27
Every function an Eigen function
Now, consider the case where the output port of the amplifier is open-circuited
( Iout  0 ):
Iin
Iout  0


Vin
oc
Vout


The (open-circuit) output voltage is therefore simply:
Vout  Z 21 Iin  Z 22 Iout
 Z 21 Iin  Z 22  0 
 Z 21 Iin
The open-circuit output voltage is thus proportional to the input current.
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
9/27
Every function an Eigen function
The proportionality constant is the impedance parameter Z 21 —a value otherwise
known as the open-circuit trans-impedance Z m :
Z m ω 
oc
Vout
ω 
Iin ω 
 Z 21ω 
Thus, an (unilateral!) amplifier can be described as:
Vin  Zin Iin
Vout  Z m Iin  Z 22 Iout
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
10/27
Every function an Eigen function
Q: What about impedance parameter Z 22 ; does it have any physical meaning?
A: It sure does!
Consider now the result of short-circuiting the amplifier output (Vout  0 ) :
Iin
sc
Iout


Vin
Vout  0


Since Vout  0 :
sc
Vout  0  Zm Iin  Z22 Iout
we can quickly determine the short-circuit output current:
sc
Iout

Jim Stiles
Z m Iin
Z 22
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
11/27
Every function an Eigen function
Q: I’m not seeing the significance of this result!?
A: Let’s rearrange to determine Z 22 :
Z m Iin
Z 22 
sc
Iout
oc
Note the numerator—it is the open-circuit voltage Vout
 Zm Iin , and so:
Z 22 
Z m Iin
sc
Iout

oc
Vout
sc
Iout
Of course, you remember that the ratio of the open-circuit voltage to shortcircuit current is the output impedance of a source:
Zout
Jim Stiles
oc
Vout
I
sc
out
 Z22
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
12/27
Every function an Eigen function
Thus, the output impedance of an (unilateral) amplifier is the impedance
parameter Z 22 , and so:
Vin  Zin Iin
Vout  Z m Iin  Zout Iout
Q: It’s déjà vu all over again; haven’t we seen equations like this before?
A: Yes! Recall the first (i.e., input) equation:
Vin  Zin Iin
is that of a simple load impedance:
Iin

Vin  Zin Iin
Vin
Z L  Zin

Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
13/27
Every function an Eigen function
And the second (i.e., output) amplifier equation:
Vout  Zm Iin  Zout Iout
is of the form of a Thevenin’s source:
where:
Vg  Z m Iin
and
Z g  Zout
Iout
Zg


Jim Stiles
Vg

Vout
Vout Vg  Z g Iout

The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
14/27
Every function an Eigen function
We can combine these two observations to form an equivalent circuit model of
an (unilateral) amplifier:
Iin
Iout
Zout

Vin

Z in


Z m Iin

Vout

Vin  Zin Iin
Vout  Z m Iin  Zout Iout
Note in this model, the output of the amp is a dependent Thevenin’s source—
dependent on the input current!
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
15/27
Every function an Eigen function
Q: So, do we always use this equivalent circuit to model an amplifier?
A: Um, actually no.
The truth is that we EE’s rarely use this equivalent circuit (not that there’s
anything wrong with it!).
Instead, the equivalent circuit we use involves a slight modification of the
model above.
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
16/27
Every function an Eigen function
To see this modification, we first insert the first (i.e., input) equation,
expressed as:
V
Iin  in
Zin
into the second (i.e., output) equation:
Vout  Z m Iin  Zout Iout
Z
 m
Z
 in

Vin  Zout Iout

Thus, the open-circuit output voltage can alternatively be expressed in terms
of the input voltage!
Z
oc
Vout
 m
Z
 in

Vin

Note the ratio Z m Zin is unitless (a coefficient!).
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
17/27
Every function an Eigen function
This coefficient is known as the open-circuit voltage gain Avo of an amplifier:
Avo  
oc
Vout
Vin

Zm
Zin

Z 21
Z11
The open-circuit voltage gain Avo   is perhaps the most important of all
amplifier parameters.
To see why, consider the amplifier equations in terms of this voltage gain:
Vin  Zin Iin
Vout  Avo Vin  Zout Iout
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
18/27
Every function an Eigen function
The equivalent circuit described by these equations is:
Iin
Iout
Zout

Vin

Z in


AvoVin

Vout

In this circuit model, the output Thevenin’s source is again dependent—but now
it’s dependent on the input voltage!
Thus, in this model, the input voltage and output voltage are more directly
related.
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
19/27
Every function an Eigen function
Q: Are these the only two was to model a unilateral amplifier?
A: Hardly! Consider now admittance parameters.
A voltage on the input port of an amplifier will indeed produce a short-circuit
output current:
I1

V1
I2  Y21V1

Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
20/27
Every function an Eigen function
However, since amplifiers are not reciprocal, placing the same voltage at the
output will not create the equal current at the input—in fact, it will produce no
current at all!
I2

I1  0
V2

This again shows that amplifiers are unilateral devices, and so we find that the
trans-admittance parameter Y12 is zero:
Y12ω   0
Jim Stiles
(for amplifiers)
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
21/27
Every function an Eigen function
Thus, the two equations using admittance parameters simplify to:
I1  Y11 V1
I2  Y21 V1  Y22V2
with the same definitions of input and output current/voltage used previously:
Iin
Iout


Vin
Vout


Iin  Y11 Vin
Iout  Y21 Vin  Y22Vout
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
22/27
Every function an Eigen function
As with impedance parameters, it is apparent from this result that the input
port is independent from the output.
Specifically, an input admittance can be defined as:
Yin ω 
Iin ω 
Vin ω 
 Y11ω 
Note that the input admittance of an amplifier is simply the inverse of the
input impedance:
Iin ω 
1
Yin ω  

Vin ω  Zin ω 
And from this we can conclude that for a unilateral amplifier (but only because
it’s unilateral!):
Y11 
Jim Stiles
1
Z11
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
23/27
Every function an Eigen function
Likewise, the second amplifier equation:
Iout  Y21 Vin  Y22Vout
is of the form of a Norton’s source:
Iout
Ig
Zg

Vout
Iout  I g Vout Z g

where:
I g  Y21Vin
Jim Stiles
and
Zg 
The Univ. of Kansas
1
Y22
Dept. of EECS
6/27/2017
493695446
24/27
Every function an Eigen function
More specifically, we can define a short-circuit trans-admittance:
Ym
Y21
Zout
1
Y22
and an output impedance:
so that the amplifier equations are now:
Iin Vin Zin
Iout  Ym Vin Vout Zout
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
25/27
Every function an Eigen function
The equivalent circuit described by these equations is:
Iin
Iout

Vin

Z in
Ym Vin
Zout

Vout

Note in this model, the output of the amp is a dependent Norton’s source—
dependent on the input voltage.
However, this particular amplifier model is likewise seldom
used.
Jim Stiles
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
26/27
Every function an Eigen function
Instead, we again insert the input equation:
Vin 
Iin
Y11
Into the output equation:
Iout  Y21 Vin Vout Zout
Y
   21
Y
 11

 Iin Vout Zout

Note the ratio Y21 Y11 is unitless (a coefficient!).
This coefficient is known as the short-circuit current gain Ais of an amplifier:
Ais  
Jim Stiles
sc
Iout
Iin

Ym
Y11

Y21
Y11
The Univ. of Kansas
Dept. of EECS
6/27/2017
493695446
27/27
Every function an Eigen function
Thus, we can also express the amplifier port equations as:
Iin Vin Zin
Iout  Ais Iin Vout Zout
So, the equivalent circuit described by these equations is the last of four we
shall consider:
Iin
Iout

Vin

Z in
Ais Iin

Zout
Vout

In this circuit model, the output Norton’s source is again dependent—but now
it’s dependent on the input current!
Thus, in this model, the input current and output current are more directly
related.
Jim Stiles
The Univ. of Kansas
Dept. of EECS