Download Biconditionals and Definitions

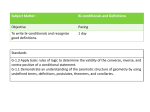
Biconditionals and Definitions Notes
Name: _______________________________________ Period ____ Date: ________________
Objective: Students will combine conditional statements and their converse in order write biconditional statements.
When a conditional and its converse are true, you can combine them as a true biconditional.
Warm-Up: Textbook Page 75 “Check Skills You’ll Need” Numbers 1 – 7
This is the statement you get by connecting the conditional and its converse with the word and.
A conditional statement and its converse can be combined to form a biconditional statement. A biconditional contains the
words "if and only if."
Writing a Biconditional
For the true conditional statement, write its converse, then if the converse is also true, combine the statements as a
biconditional.
Conditional: If two angles have the same measure, then the angles are congruent.
Converse: __________________________________________________________________
Biconditional: Two angles have the same measure if and only if the angles are congruent.
Try This! Write its converse. If the converse is also true, combine the statements as a biconditional.
Conditional: If three points are collinear, then they lie on the same line.
Converse: _______________________________________________________________________________________________
Biconditional: ____________________________________________________________________________________________
Separating a Biconditional into Parts
You can write a biconditional as two conditionals that are converses of each other.
Write two statements that form this biconditional about whole numbers:
A number is divisible by 3 if and only if the sum of its digits is divisible by 3.
Conditional: If ____________________________________________, then __________________________________________.
Converse: If ______________________________________________, then __________________________________________.
Biconditional Statements
A biconditional combines p → q and q → p as p ↔ q .
In geometry you start with undefined terms such as point, line, and plane whose meanings you understand
intuitively. Then you use those terms to define other terms such as collinear points.
A good definition is a statement that can help you identify or classify an object. A good definition has
several important components.

A good definition uses clearly understood terms. The terms should be commonly understood or already defined.

A good definition is precise. Good definitions avoid words such as large, sort of, and some.

A good definition is reversible. That means that you can write a good definition as a true biconditional.
Writing a Definition as a Biconditional
Show that this definition of perpendicular lines is reversible. Then write it as a true biconditional.
Definition: Perpendicular lines are two lines that intersect to form right angles.
Conditional: If two lines are perpendicular, then they intersect to form right angles.
Converse: If two lines intersect to form right angles, then they are perpendicular.
The two conditionals — converses of each other—are true, so the definition can be written as a true biconditional.
Biconditional: Two lines are perpendicular if and only if they intersect to form right angles.
One way to show that a statement is not a good definition is to find a counterexample.
Try This! Show that this definition of right angle is reversible. Then write it as a true biconditional.
Definition: A right angle is an angle whose measure is 90 degrees.
Conditional: __________________________________________________________________________________________
Converse: ____________________________________________________________________________________________
Biconditional: ________________________________________________________________________________________
Real-World
Connection
Is the given statement a good definition? Explain.
a.
An airplane is a vehicle that flies. The statement is not a good definition because it is not reversible. A helicopter
is a counterexample. A helicopter is a vehicle that flies, but a helicopter is not an airplane.
b.
A triangle has sharp corners. The statement is not a good definition because it uses the imprecise word sharp,
and it is not reversible.
Class Work: Textbook Pages 78 – 79 Even Numbers 2 – 40
Homework: Textbook Page 80 Numbers 41 – 46