* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 1,6,7,14,20,25,28,29,31,34,36,37,40,54,57,64
Survey
Document related concepts
Valve RF amplifier wikipedia , lookup
Negative resistance wikipedia , lookup
Power MOSFET wikipedia , lookup
Electric battery wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Rectiverter wikipedia , lookup
Electrical ballast wikipedia , lookup
Lumped element model wikipedia , lookup
Battery charger wikipedia , lookup
Current source wikipedia , lookup
RLC circuit wikipedia , lookup
Two-port network wikipedia , lookup
Current mirror wikipedia , lookup
Transcript
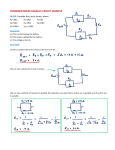
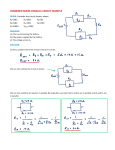
31.1. Solve: From Table 30.1, the resistivity of carbon is ρ = 3.5 × 10−5 Ω m. From Equation 31.3, the resistance of lead from a mechanical pencil is R= ρL A −5 ρ L ( 3.5 × 10 Ω m ) ( 0.06 m ) = = 5.5 Ω 2 π r2 π ( 0.35 × 10 −3 m ) = 31.6. Solve: The slope of the I versus ∆V graph, according to Ohm’s law, is the resistance R. From the graph in Figure Ex31.6, the slope of the material is ∆V 100 V = = 50 Ω I 2A 31.7. Solve: From the circuit in Figure Ex37.1, we see that 50 Ω and 100 Ω resistors are connected in series across the battery. Another resistor of 75 Ω is also connected across the battery. 31.14. Model: Assume ideal connecting wires and an ideal battery. Visualize: Please refer to Figure Ex31.14. Solve: The power dissipated by each resistor can be calculated from Equation 31.18, PR = I2R, provided we can find the current through the resistors. Let us choose a clockwise direction for the current and solve for the value of I by using Kirchhoff’s loop law. Going clockwise from the negative terminal of the battery, ∑ ( ∆V ) i = ∆Vbat + ∆VR1 + ∆VR2 = 0 ⇒ +9 V – IR1 – IR2 = 0 i ⇒ I= 9V 9V 1 = = A R1 + R2 12 Ω + 15 Ω 3 The power dissipated by resistors R1 and R2 is: PR1 = I 2 R1 = ( 31 A ) (12 Ω ) = 1.33 W 2 PR2 = I 2 R2 = ( 13 A ) (15 Ω ) = 1.67 W 2 31.20. Visualize: Please refer to Figure Ex32.20. Solve: The three resistors are in series. The total resistance of this combination is Req = R + 50 Ω + R = 2R + 50 Ω Thus, Req > 50 Ω as long as R > 0 Ω. 31.25. Model: Assume ideal connecting wires but not an ideal battery. Visualize: The circuit for an ideal battery is the same as the circuit in Figure Ex31.25, except that the 1 Ω resistor is not present. Solve: In the case of an ideal battery, we have a battery with E = 15 V connected to two series resistors of 10 Ω and 20 Ω resistance. Because the equivalent resistance is Req = 10 Ω + 20 Ω = 30 Ω and the potential difference across Req is 15 V, the current in the circuit is I= 15 V ∆V E = = = 0.5 A Req Req 30 Ω The potential difference across the 20 Ω resistor is ∆V20 = IR = (0.5 A)(20 Ω) = 10 V In the case of a real battery, we have a battery with E = 15 V connected to three series resistors: 10 Ω, 20 Ω, and an internal resistance of 1.0 Ω. Now the equivalent resistance is Req′ = 10 Ω + 20 Ω + 1.0 Ω = 31 Ω The potential difference across Req is the same as before ( E = 15 V). Thus, I′ = ∆V ′ E 15 V = = = 0.4839 A Req′ Req′ 31 Ω Therefore, the potential difference across the 20 Ω resistor is ∆V20′ = I ′R = ( 0.4839 A )( 20 Ω ) = 9.68 V That is, the potential difference across the 20 Ω resistor is reduced from 10 V to 9.68 V due to the internal resistance of 1 Ω of the battery. The percentage change in the potential difference is 10 V − 9.68 V × 100 = 3.23% 10 V 31.28. Visualize: The three resistors in Figure Ex31.28 are equivalent to a resistor of resistance Req. Solve: Because the three resistors are in parallel, ( 200 Ω ) R = 1 1 1 1 2 1 400 Ω + R = + + = + = ⇒ Req = Req R 200 Ω R R 200 Ω ( 200 Ω ) R ( 400 Ω + R ) 200 Ω 400 Ω 1+ R From this equation, we see that (i) Req = 0 Ω if R = 0 Ω and (ii) Req = 200 Ω if R → ∞. Thus, Req < 200 Ω for R < ∞. 31.29. Model: Assume ideal connecting wires. Visualize: Please refer to Figure Ex31.29. Solve: The resistance R is given by Ohm’s law, R = ∆VR I R . To determine IR we use Kirchhoff’s junction law. The input current I splits into the three currents I10, I15, and IR. That is, 2.0 A = I10 + I15 + IR = 8V 8V + + I R ⇒ IR = 2.0 A – 0.8 A – 0.533 A = 0.667 A 10 Ω 15 Ω Using this value of IR in Ohm’s law, R= 8V = 12.0 Ω 0.667 A 31.31. Model: The connecting wires are ideal with zero resistance. Solve: For the first step, the resistors 30 Ω and 45 Ω are in parallel. Their equivalent resistance is 1 1 1 = + ⇒ Req 1 = 18 Ω Req 1 30 Ω 45 Ω For the second step, resistors 42 Ω and Req 1 = 18 Ω are in series. Therefore, Req 2 = Req 1 + 42 Ω = 18 Ω + 42 Ω = 60 Ω For the third step, the resistors 40 Ω and Req 2 = 60 Ω are in parallel. So, 1 1 1 ⇒ Req 3 = 24 Ω = + Req 3 60 Ω 40 Ω The equivalent resistance of the circuit is 24 Ω. 31.34. Model: Grounding does not affect a circuit’s behavior. Visualize: Please refer to Figure Ex31.34. Solve: Because the earth has Vearth = 0 V, point d has a potential of zero. In going from point d to point a, the potential increases by 9 V. Thus, point a is at a potential of 9 V. Let us calculate the current I in the circuit before calculating the potentials at points b and c. Applying Kirchhoff’s loop rule, starting clockwise from point d, ∑ ( ∆V ) i i = ∆V9 V bat + ∆V2 Ω + ∆V3 V bat + ∆V4 Ω = 0 ⇒ +9 V – I(2 Ω) – 3 V – I(4 Ω) = 0 ⇒ I = 6V =1A 6Ω There is a drop in potential from point a to point b by an amount IR = (1 A)(2 Ω) = 2 V. Thus, the potential at point b is 9 V − 2 V = 7 V. The potential decreases from 7 V at point b to 7 V − 3 V = 4 V at point c. There is a further decrease in potential across the 4 Ω resistor of IR = (1 A)(4 Ω) = 4 V. That is, the potential of 4 V at c becomes 0 V at point d, as it must. In summary, the potentials at a, b, c, and d are 9 V, 7 V, 4 V, and 0 V. 31.36. Solve: Noting that the unit of resistance is the ohm (V/A) and the unit of capacitance is the farad (C/V), the unit of RC is RC = V C C C × = = =s A V A Cs 31.37. Model: Assume ideal wires as the capacitors discharge through the two 1 kΩ resistors. Visualize: The circuit in Figure Ex37.37 has an equivalent circuit with resistance Req and capacitance Ceq. Solve: The equivalent capacitance is 1 1 1 = + ⇒ Ceq = 1 µF Ceq 2 µ F 2 µ F and the equivalent resistance is Req = 1 kΩ + 1 kΩ = 2 kΩ. Thus, the time constant for the discharge of the capacitors is τ = ReqCeq = (2 kΩ)(1 µF) = 2 × 10−3 s = 2 ms Assess: The capacitors will be almost entirely discharged 5τ = 5 × 2 ms = 10 ms after the switch is closed. 31.40. Model: The capacitor discharges through a resistor. Assume ideal wires. Visualize: The switch in the circuit in Figure Ex31.40 is in position a. When the switch is in position b the circuit consists of a capacitor and a resistor. Solve: (a) The switch has been in position a for a long time. That means the capacitor is fully charged to a charge Q0 = C∆V = C E = (2 µF)(9 V) = 18 µC Immediately after the switch is moved to the b position, the charge on the capacitor is Q0 = 18 µC. The current through the resistor is I0 = ∆VR 9V = = 0.18 A = 180 mA R 50 Ω Note that as soon as the switch is closed, the potential difference across the capacitor ∆VC appears across the 50 Ω resistor. (b) The charge Q0 decays as Q = Q0 e−t/τ, where τ = RC = (50 Ω)(2 µF) = 100 µs Thus, the charge is Q = (18 µ C ) e−50 µs 100 µs = (18 µ C ) e−0.5 = 10.9 µ C The resistor current is I = I 0 e−t τ = (180 mA ) e−50 µs 100 µs = 109 mA (c) Likewise, the charge is Q = 2.44 µC and the current is I = 24.4 mA. 31.54. Model: Assume that the connecting wire and the battery are ideal. Visualize: Please refer to Figure P31.54. Solve: The middle and right branches are in parallel, so the potential difference across these two branches must be the same. The currents are known, so these potential differences are ∆Vmiddle = (3.0 A)R = ∆Vright = (2.0 A)(R + 10 Ω) This is easily solved to give R = 20 Ω. The middle resistor R is connected directly across the battery, thus (for an ideal battery, with no internal resistance) the potential difference ∆Vmiddle equals the emf of the battery. That is E = ∆Vmiddle = (3.0 A)(20 Ω) = 60 V 31.57. Model: The batteries are ideal, the connecting wires are ideal, and the ammeter has a negligibly small resistance. Visualize: Please refer to Figure P31.57. Solve: Kirchhoff’s junction law tells us that the current flowing through the 2.0 Ω resistance in the middle branch is I1 + I2 = 3.0 A. We can therefore determine I1 by applying Kirchhoff’s loop law to the left loop. Starting clockwise from the lower left corner, +9.0 V – I1(3.0 Ω) – (3.0 A)(2.0 Ω) = 0 V ⇒ I1 = 1.0 A ⇒ I2 = (3.0 A – I1) = (3.0 A – 1.0 A) = 2.0 A Finally, to determine the emf Ε, we apply Kirchhoff’s loop law to the right loop and start counterclockwise from the lower right corner of the loop: +Ε − I2(4.5 Ω) − (3.0 A)(2.0 Ω) = 0 V ⇒ Ε – (2.0 A)(4.5 Ω) – 6.0 V = 0 V ⇒ Ε = 15.0 V 31.64. Model: The voltage source/battery and the connecting wires are ideal. Visualize: Please refer to Figure P31.64. Solve: Let us first apply Kirchhoff’s loop law starting clockwise from the lower left corner: +Vin – IR – I (100 Ω) = 0 V ⇒ I = Vin R + 100 Ω The output voltage is Vout Vin 100 Ω Vout = (100 Ω ) I = (100 Ω ) = ⇒ R + 100 Ω V R + 100 Ω in For Vout = Vin 10 , the above equation can be simplified to obtain R: Vin 10 100 Ω = ⇒ R + 100 Ω = 1000 Ω ⇒ R = 900 Ω Vin R + 100 Ω 31.76. Model: The battery and the connecting wires are ideal. Visualize: Please refer to Figure P31.76. Solve: (a) A very long time after the switch has closed, the potential difference ∆VC across the capacitor is E. This is because the capacitor charges until ∆VC = E, while the charging current approaches zero. (b) The full charge of the capacitor is Qmax = C(∆VC)max = C E. (c) In this circuit, I = + dQ dt because the capacitor is charging, that is, because the charge on the capacitor is increasing. (d) From Equation 31.40, capacitor charge at time t is Q = Qmax(1 − e−t/τ). So, I= ( ) dQ d 1 1 −t τ E −t τ = CE 1 − e−t τ = CE e−t τ = CE e = R e dt dt τ RC A graph of I as a function of t is shown below. 31.79. Model: The battery and the connecting wires are ideal. Visualize: Please refer to Figure 31.38(a). Solve: After the switch closes at t = 0 s, the capacitor begins to charge. At time t, let the current and the charge in the circuit be i and q, respectively. Also, assume clockwise direction for the current i. Using Kirchhoff’s loop law and starting clockwise from the lower left corner of the loop, +E − iR − q dq q dq dt =0⇒E= R + ⇒ RC dq = ( EC – q)dt ⇒ = C dt C EC − q RC Integrating both sides, Q t Q dq dt t t ∫0 EC − q = ∫0 RC ⇒ − ln ( EC − q ) 0 = RC ⇒ − ln ( EC − Q ) + ln ( EC ) = RC t EC − Q EC − Q ⇒ ln =− ⇒ = e−t RC ⇒ Q = EC 1 − e−t RC RC EC EC ( Letting Qmax = EC and τ = RC, we get Q = Qmax (1 − e−t/τ). )