Download Document

Partial Solutions for 2nd Midterm
I.
Biographical Sketch – yours to do
II.
Proofs of Euclid’s Propositions: 4, 5, 10, 11, 16, 27
III.
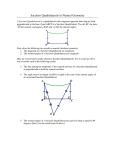
1. Describe the Saccheri quadrilateral and prove, in neutral
geometry, that the summit angles are congruent.
A Saccheri quadrilateral has one distinguished side called the base
from which the adjacent and equal edges are perpendicular to the
base. These sides are called the arms of the quadrilateral. The side
opposite the base is the summit. The angles formed by the arms
and the base are the base angles – both are right angles. The other
two angles are the summit angles.
summit
summit angle s
arm
arm
base angles
base
Give n: Sacche ri quadrilate ral ABCD with base AB.
To prove : C  D
Proof: Construct the diagonals AC and BD (Pos t. 1). Note that, by definition, A and B are both
right angles and are congruent (Pos t. 4). Also, by definition, AD=BC.
We have  ABC   BAD (SAS)  AC = BD. So,
 ADC   BCD  D  C.
D
C
A
B
2. What was Saccheri’s plan for “proving” the 5th postulate?
Saccheri knew that Euclid’s 5th postulate and the existence of a
rectangle were logically equivalent statements.
Therefore, he reasoned, if one could prove in neutral geometry that
a rectangle exists, then the 5th postulate would follow as a
consequence and so would not be independent of the first four.
Saccheri chose the quadrilateral that we have called a Saccheri
quadrilateral to prove his case. He showed, as we did above, that
the summit angles were congruent. If they were also right angles,
then the SQ would be a rectangle. He posed the three possible
hypotheses for the summit angles: 1) Both angles are obtuse, 2)
both angles are acute, or 3) both angles are right angles. If he could
show that cases 1 and 2 were impossible then, by elimination, the
third case would have to hold.
Saccheri easily disposed of the obtuse case, but worked much
harder in coming up with a (as it turns out flawed) contradiction
for the acute angle case.
3.
State the Saccheri-Legendre Theorem and describe how Saccheri used
it in his attempt to “prove” the 5th postulate.
S-L Theorem: The angle sum of any triangle can not exceed two right
angles.
Saccheri noted that if the summit angles of a Saccheri quadrilateral
ABCD were obtuse then at least one of the triangles ABC
or ADC would have an angle sum exceeding 2 right angles, contrary
to the S-L Thm.
4. Assuming Saccheri’s Acute Angle Hypothesis, show that the summit of a
Saccheri quadrilateral is longer than the base.
Give n: Sacche ri quadrilate ral ABCD with base AB.
To prove : DC > AB.
Proof: Construct the diagonals midline of the S.Q. MN which we know to be pe rpe ndicular
to the summit and the base . Since M and N are midpoints of CD and AB, respective ly, then
AB will be re late d (<, =, >) to CD as CM is related to BN. The re are thre e possibilitie s to conside r:
1) CM = BN (summit equals the base )
2) CM < BN (summit shorter than the base )
3) CM > BN (summit gre ater than the base )
We will e liminate the first two possibilitie s.
Suppos e CM = BN. The n MNBC is a S.Q. with base MN. But this implie s that C  B.
But C is acute and B is right. This is a contradiction,  cas e 1) does not hold.
Suppos e CM < BN. The n the re is a point P on NB such that NP = MC. The n MNPC is a S.Q.
with bas e MN. This implie s that MCP  NPC. Since C is acute , then MCP is as well.
On the other hand, mNPC > B (as it is an e xte rior angle of  PBC, Prop. 16). So NPC is obtus e.
Since an acute angle ( MCP) can't be congrue nt to an obtus e angle ( NPC), we have a contradiction.
Thus, case 2) doe sn't hold eithe r.
The refore, CM > BN and the s ummit is longer than the base .
IV.
D
M
A
N
C
P
B
1. Assuming you are given segments of length a, b, and 1, sketch
out the basic constructions for each of the following:
a
ab
etc.
(See these notes
)
2. Define and give two examples for each of the following:
Constructible number: A real number c is constructible if a segment
of length |c| can be constructed from a unit
segment using only a compass and straightedge.
Examples: -3, 1, 5/2, √12
Field: A field is a triple (F, +,*) consisting of a set F and two
operations that satisfies the closure, commutative, associative,
identity and inverse properties for both operations and right and
left distributivity for * over +.
Alternatively, for our purposes, a field is a subset of real
numbers that is closed under the four arithmetic operations
(excluding division by 0).
Examples: (Q, +,*)
(R, +, *)
and multiplication mod 5
Z5 with addition
Quadratic field extension: Let F be a field and k an element of F for
which √k is not in F. Then the quadratic extension
of F, denoted F(√k ) is ….
… the smallest field containing
both F and √k .
or
… the intersection of all fields
containing both F and √k .
or
… the field { a + b√k : a, b
are in F }.
Examples: Q(√2) is a quadratic extension of the
rationals
C (the complex numbers) is a quadratic
extension of R
3. Describe pictorially the three classical impossible
constructions. See these notes
4. Outline the proof that the cube root of 2 is not constructible.
a.
Suppose 3 2 is cons tructible , the n it lies in the terminal field of some
quadratic exte ns ion se ries Q = F0 F1 F2 ... Fn.
b. Show that if 3 2 lie s in the quadratic exte ns ion of some fie ld F, the n it
lies in F as well.
c. Conclude that s ince
d.
3
e.
The refore,
3
2 lie s in Fn the n by descent it is in Q.
2 is not rational, however, so this is a contradiction.
3
2 is not constructible.