Download Geometry Performance Expectations by reporting Strand Reporting

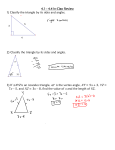
Geometry Performance Expectations by reporting Strand
Reporting Strands
Logical arguments and proof
Proving and applying properties of 2-dimensional
figures
Figures in a coordinate plane and measurement
Course-Specific content
Performance
Expectations
G.1.D
G.1.E
G.1.F
G.3.A
G.3.B
G.3.C
G.3.D
G.3.E
G.3.F
G.3.G
G.4.B
G.4.C
G.6.E
G.6.F
G.1.A
G.2.A
G.2.B
G.2.C
G.2.D
G.3.B
G.3.H
G.3.I
G.3.J
G.3.K
G.4.A
G.4.D
G.5.A
G.5.B
G.5.C
G.5.D
G.6.A
G.6.C
G.6.D
Anticipated
number of
questions
6-8
21-24
7-9
6*
Question
1.
Determine the value of x if
ΔABC is equilateral.
PE
G.3.A
Answer
G.1.D
C: If you are a pet owner, then you
have a dog. False, you could have a
hamster.
G.2.B
D: m  4 + m  6 = 180
B
6x + 3
7.5x
A
C
10x – 5
Write your answer on the line.
2. Write the converse of the
conditional statement.
Determine if the converse
is true or false. If it is
false, find a
counterexample.
“If you have a dog, then you are a
pet owner.”
3. Given a║b, determine
which equation must be
true.
a
3
b
7
1 2
4
5 6
8
4.
Determine measure of
angle 2.
Write your answer on the line.
G.3.A
m  2=50˚
70°
2
1
60° 3 4
40°
5.
ΔDEF has vertices D(4, 1),
E(2, –1), and F(–2, –1).
Classify ΔDEF based on its
sides.
G.4.C
C: scalene
Determine the equation of a
line through the point
(3, –4) that is perpendicular
to the line y = 3x + 7.
G.4.A
Joe and Sara were standing
on a pier sailing a toy sail
boat. The boat was 6 feet
from the base of the pier
and the pier was 4 feet
above the water.
O 6 ft
G.3.A
6.
7.
C:
˚
A
4 ft
B
T
Determine the angle of
depression from the pier to
the toy sail boat.
Show your work using
words, numbers and/or
diagrams.
8.
Joanna’s teacher said “The
diagonals of a square bisect
each other.”
Joanna drew this figure and said
“The diagonals of this figure bisect
each other, so it must be a square.”
Joanna made an error in her
mathematical argument. What is
the error?
G.1.E
B: In the figure Joanna drew, the
diagonals do not bisect each other.
9.
Determine the midpoint of
G.4.B
JK , where J(–1, 2) and
K(6, 8).
10. Look at the diagram.
K
B: ( 2
1
, 5)
2
G.3.B
C: Angle-Side-Angle Congruence
G.4.B
Q (-2, 0)
G.1.A
B: This is an example of inductive
M
L
J
N
What theorem or postulate can you
use to prove
?
11. Three vertices of a square
have coordinates (3, 1), (4,
-4) and (-1, -5). The
diagonals of the square
intersect at point Q.
Determine the coordinates of point
Q.
12. 3, 5, 7, and 11 are prime
numbers. 4, 6, 8, 9, and 10
are composite numbers.
Tiana makes the conjecture
that prime numbers must be
odd.
Which statement is true?
13. One leg of a
reasoning and the conjecture is not
valid.
G.3.C
triangle is
8 cm long.
Determine the length of the
hypotenuse.
B:
G.1.D
14. Look at the conditional
statement.
C: If an angle is acute, then it
measures 30 .
“If an angle measures 30 , then it is
acute”
Which statement is the converse?
15. Which equation represents
the line through the points
(-1, -2) and (2, 7)?
G.4.A
A: y = 3x + 1
16. Which statement is true
about all parallelograms?
G.3.F
C: The diagonals bisect each other.
17. Quadrilateral ABCD is a
rhombus and m∠BCE =
50 .
G.3.G
m∠EBC=40˚
G.1.D
D: If a figure is not a pentagon, then
A
B
E
D
C
Determine the m∠EBC.
18. Look at the conditional
statement.
it does not have five sides.
“If a figure is a pentagon, then it has
five sides”
Which statement is the inverse?
19. Triangle JKE is an obtuse
isosceles triangle with
m∠E = 10 and
.
G.3.A
B: 160
G.3.B
Statement 5: m∠ABD= m∠CBE
What is the m∠J?
20. A proof is shown.
Fill in the blanks for steps 5 and 6 to
complete the proof.
Given:
Prove:
B is the midpoint of
B is the midpoint of
Reason 6: SAS congruency
.
.
.
21. Which ordered pair is the
midpoint of the line
segment with endpoints
(2,-5) and (-6, 4)?
G.4.B
C:
22. The diagonal of a square is
7 cm.
G.3.C
D:
G.1.F
A: A postulate is accepted as true
24. Two unique planes
intersect. Which geometric
term describes the
intersection?
G.2.D
without proof.
A: line
25. Look at the diagram.
G.3.F
C: a = 13.5, b = 106
7 cm
Determine the length of one side of
the square.
23. Which statement is true?
Determine the values for a and b
that would make the quadrilateral a
parallelogram.
26. Look at the triangle.
18
13
5
y
G.3.D
Determine the length of y. Express
your answer in simplified radical
form.
27. Lines l, m, and n lie in the
same plane. Line m is
perpendicular to line l.
Line n is perpendicular to
line l.
Which statement is true?
G.2.A
While walking around
Seattle, Mary climbed
several steep streets.
One of the steepest
streets, Roy Street, has
a slope angle of 11.9°
according to the tour
guide. After walking
100 feet up the hill,
she wanted to
determine how high
she had climbed.
G.3.E
28.
11.9°
B: Line m and line n are parallel.
Rounded to nearest foot: 21 ft
100 feet
Height climbed
Horizontal distance
Use a trigonometric ratio
(sine, cosine, tangent) to
determine how high Mary
climbed.
Be sure to write the
equation and show the
steps you used to solve the
equation. Round your
answer to the nearest foot.
29. Determine how many
miles a person will run
G.6.F
≈3.1 miles
during a 5-kilometer race.
Write your answer on the
line.
1 km ≈ 0.62 mi
30. Which statement is an
example of inductive
reasoning?
G.1.A
B: Squares have equal sides. This
31. The rhombus QRST is
made of two congruent
triangles. Given m  QRS
= 34° determine the
measure of  S.
Q
G.3.F/G.3.G
figure has equal sides, therefore this
figure is a square.
C: 112°
R
S
T
32. Determine whether the
conjecture is true or false.
Give a counterexample for
a false conjecture.
G.1.E
False. Any three points define a
plane. Points A, B, and C define a
unique plane. Point D does not
have to be on this plane.
Given: points A, B, C, and D
Conjecture: A, B, C, and D are
coplanar
33. Identify the congruent
triangles in the diagram and
write a congruence
statement.
G.3.B
B: Δ LSK  Δ MSN
G.3.E
D:
M
L
S
K
N
34. Determine cos I in ΔGHI.
G
75
21
I
H
72
35. Write the contrapositive of
the conditional statement.
G.1.D
C: Non-supplementary angles and
not two angles measuring 180
degrees. True
Determine if the
contrapositive is true or
false. If it is false, find a
counterexample.
“Two angles measuring 180 degrees
are supplementary”
36. Complete this chart.
G.3.J
37. Determine which
statement is a property of
all rectangles.
G.3.G
Triangular Prism:
Edges:9, faces:5, vertices: 6
Square Pyramid:
Edges: 8, faces:5, vertices: 5
Cube:
Edges:12, faces:6, vertices:8
Hexagonal Pyramid:
Edges:12, faces:7, vertices:7
Hexagonal Prism:
Edges:18, faces:8, vertices:12
D: Four right angles.
38. The figure is a rectangular
prism with dimensions 12
inches long, 5 inches wide
and 7 inches tall.
Determine the length of
G.3.D
BI=
BI .
BI≈14.76 inches
B
C
A
D
7
G
F
5
H
I
12
Write your answer on the
line.
39. Given B(–4, –6),
determine which reflection
would result in B’(6, 4).
G.5.A
40. Determine the exact length
of x in ΔHJK.
G.3.C
C: Reflected over the line y = –x.
C: 10
K
60°
x
J
5
30°
H
41. If you are going 50 miles
per hour, determine how
many feet per second you
are traveling.
42. The ratio of a pair of
corresponding sides in two
similar triangles is 5:3.
The area of the smaller
triangle is 108 in2. What is
the area of the larger
triangle?
G.6.F
43. Jessie is working on the
roof of her house. She has
measured the angle of the
roof and the length of the
roof. Determine the width
of the house, w.
G.3.E
15 ft.
G.6.D
15 ft.
w
44. The segment bisector is the
midpoint.
G.1.D
45. ΔRST has vertices R(3, 3),
S(6, –2), and T(0, –2).
Classify ΔRST based on its
sides.
G.4.C
46. Look at the given
information for
quadrilateral ABCD.
G.7.E/G.3.G
A
C
is not parallel to


Draw and label a shape that
satisfies all of the given
information.
Determine the most specific
name for the shape.
47. Martina has a calculator
box that has a volume of 29
Inverse: The non-segment
bisector is not the midpoint
True
A: isosceles
»
»
Isosceles Trapezoid
G.6.F
B
D
cubic inches.
1 inch = 2.54 centimeters
Determine the volume of the
calculator box to the nearest cubic
centimeter.
48. Determine the image of
Y(–4, 7) under the
translation of :
(x, y)  (x + 3, y – 5).
G.5.B
A: Y(–1, 2)
49. Look at the figure.
G.3.B
A: FH = 12
What additional information do you
need to show the triangles below
are similar using the Side-Angle-Side
Similarity Theorem?
E
G
18
8
F
10
D
12
H
50. Find sin C as a decimal
rounded to the nearest
hundredth.
C
8.3
A
G.3.E
D: 0.87
16.9
B
14.7
51. Two similar figures have a
ratio of volumes of 64:27.
What is the ratio of
similarity?
G.6.D
52. Michael is 5 feet tall.
Michael measures his
G.3.B
Ratio of Similarity is 4:3
shadow as 8 feet long. A
tree in his backyard has a
shadow that is 25 yards
long. How tall is the tree?
5 ½ ft
8 ft
G.1.E
53. Look at the pair of
triangles.
to determine similarity or
congruence.
B
A
D: There is not enough information
D
C
Which statement is true?
54. Steven built a box for his
vegetable garden in the
shape of a rectangular
prism. The volume of the
vegetable garden was 24
cubic feet. He built another
garden box that was two
times longer and two times
higher. He thinks the
volume will be twice as
much. Explain why Steven
is not correct.
G.6.D
Original box volume: xyz
New box volume: (2x)(2y)(z)= 4xyz
If Steven wanted to double the
volume of his garden, he would
need to double only one of the
dimensions (probably the length
or width)
If Steven wants his second garden
box to have twice the
volume, what should he do
instead?
55. To the nearest degree,
what is m∠G?
Steven is not correct. By doubling
two dimensions, he has created a
rectangular prism with 4 times the
volume.
G.3.E
B: 57
G.4.B
D: L (8, 3)
E
12.
1
F
7.8
G
56. JKLM is an isosceles
trapezoid with J(0, –1), K(–
2, 3) and M(6, –1).
Determine the coordinates
of L.
57. Given a║b, determine
which relationship must be
true.
a
3
b
7
G.2.B
B:  2 and  8 are supplementary.
G.3.B
C:
1 2
4
5 6
8
58. Determine which triangle
is similar to ΔDEF.
36
D
13
39
5
E
12
59. Name all segments skew to
B
BC .
A
F
G.1.F
C
D: GF , HI , DI , AF
D
H
G
I
F
60. Determine which theorem
or postulate can be used to
prove that these two
triangles are similar.
G.3.B
A: AA
8
63°
4
27°
6
61. Cody is standing 14 feet
from the base of the tree.
The top of the tree makes a
G.3.C
15
60 angle with the ground
at the point where he is
standing.
60
14 ft
Determine the height of the tree.
Round your answer to two decimal
places.
G.2.B
62. Given a║b
m  3 = 5x + 10 and
m  5 = 3x + 10,
determine the value of x.
1 2
3 4
a
b
7
63. In circle C, m AB = 72.
Determine m  BCD.
C: 20
5 6
8
m  BCD=108˚
G.3.H
A
C
Write your answer on the line.
D
B
64. Determine which set of
measures could represent
the sides of a right triangle.
65. Determine the exact value
of x in ΔLMN.
N
x
L
66. ΔRST has vertices R(3, 3),
S(6, –2), and T(0, –2).
Classify ΔRST based on its
G.3.D
D: 9, 12, 15
G.3.C
C: 25 3
50
60°
G.4.C
M
A: isosceles
sides.
67. In the diagram:
G.3.B
Statement
Given: AB  EB
A
Prove:
D  C
ABD  CBE
D  C
ABD  EBC
C
B
∆DBA≅∆CBE
D
E
68. Determine the value of y.
G.3.H
D: 4.5
G.3.G
C: 90°
3
6
y
9
69. For rhombus GHJK,
determine m  1.
G
H
1
K
J
70. Given quadrilateral XYWZ,
determine whether
G.4.C
WX and YZ are parallel,
perpendicular or neither.
W(0, –3), X(–1, 5), Y( 2, 5) Z(–1, 2)
71. Determine the value of x
and y so that QRST will be
a parallelogram.
Neither
G.3.F/G.3.G
A: x = 6, y = 42
Q
R
24°
(y-10)°
32°
4x°
T
S
Justification
Given
Given
Vertical
angles are
congruent
AAS
congruency
72. Two angles measuring 90°
are complementary.
G.1.D
73. Which statement is an
example of deductive
reasoning?
G.1.A
74.
G.3.B
If
Inverse: Two angles whose sum is
not 90˚ are not complementary
True
B: Dogs are mammals. Mammals
breathe oxygen. Therefore dogs
breathe oxygen.
B
AF  DE , AB  FC and
C: SAS
C
AB ║ FC , determine which
theorem or postulate can be
used to prove
ABE  FCD .
A
75. Identify which of the
following is a property of a
parallelogram.
G.3.F
F
E
D
D: The diagonals bisect each other.