Download Lab 4

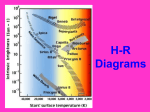
Astronomy 115
Name:
Lab 4: Light and spectroscopy
Purpose: In this lab, you’ll discover how astronomers calculate the magnitude of a star
as a measure of its intensity, and how the color of light can be used to determine
properties of the body it leaves.
Astronomical magnitudes
Hipparchus, in the second century BCE, decided that a star of magnitude one (first
magnitude — as bright as some of the brightest stars in the sky) should be 100 times as
bright as a star of magnitude six (sixth magnitude — the limit of human vision). This
works out to be a 2.512 times increase in brightness for every lower magnitude
(Hipparchus didn’t work this out — this work was done in the eighteenth century CE).
So the magnitude scale is a logarithmic scale, just like the Richter scale for earthquake
magnitudes.
From the previous lab, copy the intensity data, or obtain new data to fill table 4.1 below.
1. The formula for calculating any type of (light intensity) magnitude is:
Magnitude = –2.5 × log10(intensity of object)
Fill in the magnitude column in the table.
Table 4.1: Magnitudes
Bulb
Low wattage placed at a
distance of 30 cm
High wattage placed at a
distance of 90 cm
Bulb
Photocell
intensity (lux)
Apparent
visual
magnitude
Photocell
intensity
Absolute visual
magnitude
Low wattage placed at a
distance of 60 cm
High wattage placed at a
distance of 60 cm
2. Which type of visual magnitude (absolute or apparent) is used to describe stellar
and other astronomical object luminosity from Earth? Why is this type misleading when
trying to determine the actual stellar luminosity?
3. In summary: the brighter the star appears, the __________________ its
magnitude.
Figuring out a color index
Photometry is the determination and use of the color spectrum of astronomical
objects to determine the objects’ properties. Two properties you will investigate later are
distance and age. The objects you will use are stars in various clusters in the Milky Way
galaxy and beyond. This is known as the Color Index method of distance determination.
As you will see, the color of a star is related to its temperature. So to figure out how far away
or how old a star is, one needs to agree to a color index which anyone can use and will not
be affected by the distance to the star (remember, the star should get dimmer when it’s
further away, not change color!).
With the advent of colored filters in color photography, this idea became easier to
implement. One could take color time-exposure photos of the stars using various filters
and then compare the results.
Needed:
• the datalogger with the photocell attached
• an incandescent lamp and a fluorescent lamp
• a blue and a yellow gel
4. Light the incandescent lamp and measure its intensity without any of the color filters
(don’t worry about the background correction for this part). Enter the value in the table
below. Then use the appropriate color gel to find the values of intensity for the colorfiltered light (use the same lamp!), and enter that data. Use the formula from the
previous section to calculate the magnitudes. Repeat for the fluorescent lamp.
Incandescent bulb
No filter
Yellow filter (V value)
Blue filter (B value)
Fluorescent bulb
No filter
Yellow filter (V value)
Blue filter (B value)
Photocell
intensity (lux)
Visual magnitude
In the early twentieth century, it was shown that if one measured the magnitude of star’s
brightness using an image of the star taken with a yellow filter (problem 4a — call this the
V or visual index) and if one did the same with a blue filter (problem 4b — the B or
blue index), then the quantity B-V (B minus V) could be related to the star’s
temperature. This is the B-V color index.
5. Calculate B minus V for each lamp, enter it into the table below. Then find the
package for the bulb and read off the temperature of the bulb. The units of the
temperature are Kelvins (K), which is simply the degrees Centigrade plus 273 (i.e., K =
°C + 273)
B – V color index
Bulb temperature
(K)
Incandescent bulb
Fluorescent bulb
6. Granted that you only checked two bulbs, but is there a general rule about the sign (or
relative size) of B–V and temperature? In other words, complete the sentence:
“The hotter the bulb, the ___________________________ the B–V color index.”
7. a. Generalize to stars: Given a red star and a blue star of equal magnitude (apparent
brightness) and given a yellow filter, which would appear brighter?
b. Given a red star and a blue star of equal magnitude (apparent brightness) and given a
blue filter, which would appear brighter?
c. So which color stars would have negative B-V index numbers? Which color stars
would have positive B-V index numbers?
d. Using your rule in question 6, the stars that have negative B-V index numbers tend
to be hotter or cooler? The stars that have positive B-V index numbers tend to be
hotter or cooler?
A very basic correlation using the color index
By the 1920’s, various astronomers had evidence that the temperature of a star was also
related to the star’s luminosity (the intrinsic “brightness” of a star). So, to quantify the
luminosity without using non-standard brightness units, astronomers developed the
absolute magnitude scale, which is the magnitude of a star if it could be viewed from
a standard 10 parsecs away). This takes away the distance-dimming effect. When the
absolute magnitude (M) was plotted against the B-V index for lots of stars, the
correlation became apparent.
For instance, for a particular star cluster, these data were derived:
Star
Number
133
165
522
980
1234
1266
1305
1355
1432
1766
1797
1040
2406
2601
Brightness
in Visual
Magnitudes
Color
B-V
14.4
7.6
11.9
4.2
6.8
8.3
13.5
14.0
2.9
9.1
10.1
15.8
11.1
15.0
1.28
0.12
0.90
-0.10
-0.02
0.32
1.14
1.19
-0.13
0.43
0.52
1.44
0.72
1.51
8. Plot the B-V color index (x-axis) versus the absolute brightness in visual magnitudes
(y-axis) on standard graph paper. One weird thing: put 0 high up on the y-axis, and
number sequentially downwards. Make sure you have room for the negative B-V
values. Remember to label axes and title the graph.
9. Using an appropriate diagram in your textbook, label the various areas of your
diagram that classify the various stars.
Introduction to spectroscopy
You’ve now seen that stars seem to group into various parts of the Hertzsprung-Russell
diagram. The next step is to ask “Why do they do that?”, which leads to the question:
“Well, what are they made of?” In fact, how do astronomers know anything about parts
of the solar system and universe that we (humans or the probes we send) have never
physically touched? The answer lies in the light that is emitted or reflected by an
astronomical object.
In this part of the exercise, you will experimentally investigate objects that emit light
energy and objects that absorb light energy, and how you measure this absorption or
emission. To do this, you will need to know the term “electromagnetic spectrum”
which is the whole range of energies (wavelengths, frequencies) that light can have. For
this experiment, we will be interested primarily in the visible spectrum, a tiny subset of
the electromagnetic spectrum.
The device you will use to measure the spectrum is the spectroscope (called the
SCSpec in this experiment), which is basically a smart prism. A prism because, like its
glass cousin, it separates light into its component colors (ROYGBV), and smart, because
it can tell you what wavelengths are present in the spectrum.
Using the spectroscope — Work in groups of three or four.
Needed:
• Laptop computer from the cart
• SCSpec spectroscope kit
• Various light sources (incandescent, UV and hydrogen gas)
Set up the spectroscope and laptop as stated in the laminated sheet that comes with the
spectroscope kit. Make sure that you have a Desktop visible on the laptop before you
plug the USB cable from the spectroscope into the laptop. Make sure the spectroscope is
actually plugged into an electrical socket.
Follow the instructions on the laminated sheet to start up the software “SCSpec”. After
clicking on the “Connect” button, it should quickly turn into a “Disconnect” button. If
this does not happen, let me know! You should see a rainbow-like set of colors appear on
the left of the screen.
Do not worry about “Calibration”; after setup, go directly to the back of the sheet to
“Capturing Spectra”. You will not need to Save any of the data you collect since you’ll be
writing it down, but you will need to make sure that Graph is visible. After clicking
“Graph”, you should see a graph appear on the right of the screen.
10. a. Look at the graph and state what quantity the x-axis represents, and what units
that quantity is in. Hint: see diagram on first page of this handout.
b. What quantity does the y-axis represent, and why might the units not be so helpful for
this quantity? What does a high value (“peak”) of this quantity mean?
11. Take the laptop and spectroscope outside (please be careful not to drop anything),
and use the extension cord to plug in the spectroscope. Point the spectroscope at a piece
of white paper that is reflecting sunlight. DO NOT POINT THE SPECTROSCOPE
DIRECTLY AT THE SUN; the results are not useful. Sketch the graph below, giving
numbers on the x-axis where useful.
12. While still outside, point the spectroscope at nearby shrubbery and sketch that graph
below, again giving numbers on the x-axis where useful.
13. Indoors, point the spectroscope at the fluorescent light. Sketch the graph below,
giving numbers on the x-axis where useful.
14. Point the spectroscope at one of the incandescent bulbs. Sketch the graph shown
on the display below, giving numbers on the x-axis where useful.
15. Would you categorize the Sun’s spectrum as “continuous” or “discrete”? Which bulb,
incandescent or fluorescent, yields a more “Sun-like” spectrum? Therefore, which bulb
would one use in a light box to ward off seasonal-affective disorder (SAD)?
16. a. Do the Sun, light bulbs, and UV lamps absorb or emit light? Call these light
sources.
b. Do surfaces like the table or the shrubbery absorb or emit light? Call these light sinks
(or absorbers). How can you tell without using a spectroscope that they do?
17. Now place a piece of blue gel and a piece of red gel in front of the light bulb, and
sketch the graph on the display. Label the graph on the x-axis where there is (are)
“peak(s)”.
18. Obtain a hydrogen gas lamp, and sketch the graph on the display. Label the graph
on the x-axis where there is (are) “peak(s)”.
19. The graphs you obtained from the red/blue gel and from the hydrogen gas lamp
should be similar (not identical, anyway); both should have “peaks” in the red part of the
spectrum and the blue part. Explain how these two are fundamentally different
experiments. In other words, even though the graphs are similar. what sample is
creating the graph in #17, and how? What sample is creating the graph in #18, and
how?
20. The Sun and other stars will have an origin more similar to #17, or to #18? Explain
your answer in light of how we know stars work.
21. Obtain the ultraviolet (UV) box and carefully point the spectroscope up at the UV
light. DO NOT LOOK AT THE ULTRAVIOLET LIGHT YOURSELF unless you wish to
have cataracts. Sketch the graph below, giving numbers on the x-axis where useful. Why
did you obtain the result that you did?