Download Statistics for Managers Using Microsoft Excel, 3/e

Statistics for Managers
Using Microsoft Excel
(3rd Edition)
Chapter
Basic Probability and Discrete
Probability Distributions
Chapter Topics

Basic probability concepts


Conditional probability


Sample spaces and events, simple probability, joint
probability
Statistical independence, marginal probability
Bayes’s Theorem
Chapter Topics

(continued)
The probability of a discrete random variable

Covariance and its applications in finance
Binomial distribution

Poisson distribution

Hypergeometric distribution

Sample Spaces

Collection of all possible outcomes

e.g.: All six faces of a die:

e.g.: All 52 cards in a deck:
Events

Simple event



Outcome from a sample space with one
characteristic
e.g.: A red card from a deck of cards
Joint event


Involves two outcomes simultaneously
e.g.: An ace that is also red from a deck of
cards
Visualizing Events

Contingency Tables
Ace

Tree Diagrams
Full
Deck
of Cards
Not Ace
Total
Black
Red
2
2
24
24
26
26
Total
4
48
52
Ace
Red
Cards
Black
Cards
Not an Ace
Ace
Not an Ace
Simple Events
The Event of a Triangle
There are 5 triangles in this collection of 18 objects
Joint Events
The event of a triangle AND blue in color
Two triangles that are blue
Special Events
Null Event

Impossible event
e.g.: Club & diamond on one card
draw


Complement of event



For event A, all events not in A
Denoted as A’
e.g.: A: queen of diamonds
A’: all cards in a deck that are
not queen of diamonds
Special Events

Mutually exclusive events


Two events cannot occur together
e.g.: -- A: queen of diamonds; B: queen of clubs


(continued)
Events A and B are mutually exclusive
Collectively exhaustive events



One of the events must occur
The set of events covers the whole sample space
e.g.: -- A: all the aces; B: all the black cards; C: all the
diamonds; D: all the hearts
Events A, B, C and D are collectively
exhaustive
 Events B, C and D are also collectively
exhaustive

Contingency Table
A Deck of 52 Cards
Red Ace
Ace
Not an
Ace
Total
Red
2
24
26
Black
2
24
26
Total
4
48
52
Sample Space
Tree Diagram
Event Possibilities
Full
Deck
of Cards
Red
Cards
Ace
Not an Ace
Ace
Black
Cards
Not an Ace
Probability



Probability is the numerical
measure of the likelihood
that an event will occur
1
Certain
Value is between 0 and 1
Sum of the probabilities of
all mutually exclusive and
collective exhaustive events
is 1
.5
0
Impossible
Computing Probabilities

The probability of an event E:
number of event outcomes
P( E ) 
total number of possible outcomes in the sample space
X

T
e.g. P(
) = 2/36
(There are 2 ways to get one 6 and the other 4)

Each of the outcomes in the sample space is
equally likely to occur
Properties of Probability


If A is an event and A’ is its complement
then P(A) = 1-P(A’)
For any two events A and B P(AUB) = P(A)
+ P(B)-P(AB)
A
B
A=(AB)U(AB’)
P(A)=P(AB)+P(AB’)
P(AUB)=P(B)+P(AB’)
= P(B)+P(A)-P(AB)
Properties of Probability

If A subset of B then
P(A)≤P(B)
B
A
B  A   A' B 
P( B)  P( A)  P( A' B)
P( B)  P( A)
Properties of Probability
P( A  B  C )  P(( A  B)  C )
 P( A  B)  P(C )  P(( A  B)  C )
 P( A)  P( B)  P( A  C )  P(C ) 
P(( A  C )  ( B  C ))
 P( A)  P( B)  P( A  C )  P(C ) 
P(( A  C )  P( B  C ))  P( A  B  C )
Properties of Probability
P(i 1 Ai )   P( Ai )   P( Ai  A j ) 
n
i j
i
 P( A  A  A )  .... 
i
i j k
 1
n 1
j
n
P(i 1 Ai )
k
Computing Joint Probability

The probability of a joint event, A and B:
P(A and B) = P(A  B)
number of outcomes from both A and B

total number of possible outcomes in sample space
E.g. P(Red Card and Ace)
2 Red Aces
1


52 Total Number of Cards 26
Joint Probability Using
Contingency Table
Event
B1
Event
B2
Total
A1
n(A1 and B1) n(A1 and B2) n(A1)
A2
n(A2 and B1) n(A2 and B2) n(A2)
Total
n(B1)
n(B2)
N(S)
Joint Probability
Marginal (Simple) Probability
Joint Probability Using
Contingency Table
Event
B1
Event
B2
Total
A1
P(A1 and B1) P(A1 and B2) P(A1)
A2
P(A2 and B1) P(A2 and B2) P(A2)
Total
P(B1)
P(B2)
1
Joint Probability
Marginal (Simple) Probability
Computing Compound
Probability

Probability of a compound event, A or B:
P( A or B)  P( A  B)
number of outcomes from either A or B or both

total number of outcomes in sample space
E.g.
P(Red Card or Ace)
4 Aces + 26 Red Cards - 2 Red Aces

52 total number of cards
28 7


52 13
Compound Probability
(Addition Rule)
P(A1 or B1 ) = P(A1) + P(B1) - P(A1 and B1)
Event
Event
B1
B2
Total
A1
P(A1 and B1) P(A1 and B2) P(A1)
A2
P(A2 and B1) P(A2 and B2) P(A2)
Total
P(B1)
P(B2)
1
For Mutually Exclusive Events: P(A or B) = P(A) + P(B)
Computing Conditional
Probability

The probability of event A given that event B
has occurred:
P( A and B)
P( A | B) 
P( B)
E.g.
P(Red Card given that it is an Ace)
2 Red Aces 1


4 Aces
2
Conditional Probability
Event
Event
B
B’
Total
A
P(A and B)
P(A1 and B’) P(A)
A’
P(A’ and B)
P(A’ and B’) P(A)
Total
P(B)
P(B’)
P( A and B)
P( A | B) 
P( B)
1
Conditional Probability Using
Contingency Table
Color
Type
Red
Black
Total
Ace
2
2
4
Non-Ace
24
24
48
Total
26
26
52
Revised Sample Space
P(Ace and Red) 2 / 52
2
P(Ace | Red) 


P(Red)
26 / 52 26
Example

A family has two children. What is the
conditional probability that both are boys
given that at least one of them is a boy ?
Assume that the sample space S is given by
S={(b,b),(b,g),(g,b),(g,g)}, and all outcomes
are equally likely. [(b,g) means for instance
that the older child is boy and the younger
child is a girl.]
Solution

Letting E denote the event that both children
are boys, and F the event that at least one
of them is a boy, then the desired probability
is given by
P( E | F ) 
P ( EF )
P( F )

P ({( b ,b )})
P ({( b ,b ),( b , g ),( g ,b )})

1/ 4
3/ 4
 1/ 3
Example

Bety can either take a course in mathematics
or in statistics. If She takes the statistic
course, then she will receive an A grade with
probability ½ , while if she takes the math
course then she will receive an A grade with
prob. 1/3 . Bety decides to base her
decision on the flip of fair coin. What is
the prob that Bety will get an A in math ?
Solution

If we let F be the event that Bety takes math
and E denote the event that she receives an
A in whatever course she takes, then the
prob is P(EF) = P(E|F)P(F) = 1/3.1/2 =
1/6.

P(F) =1/2 , because Bety decides to base her
decision on the flip of fair coin.
Example

Suppose that each of three men at the party
throws his hat into the center of the room.
The hats are first mixed up and then each
man randomly selects a hat. What is the
probability that none of the three men selects
his own hat ?
Solution

Let us denote by Ei ,i=1,2,3, the event that
the ith man selects his own hat. The
probability that none selects his own hat is
1  P( E1  E2  E3 )

Now we compute
P( E1  E2  E3 )
P( Ei )  13 , i  1,2,3
P( Ei E j )  P( Ei | E j ) P( E j )
 12  13 
1
6
P( Ei E j Ek )  P( Ek | Ei E j ) P( Ei E j )
1. 16
3
P(i 1 Ei )  3  13  3  16  16 
2
3
Conditional Probability and
Statistical Independence

Conditional probability:
P( A and B)
P( A | B) 
P( B)

Multiplication rule:
P( A and B)  P( A | B) P( B)
 P( B | A) P( A)
Conditional Probability and
Statistical Independence
(continued)

Events A and B are independent if
P( A | B)  P ( A)
or P( B | A)  P( B)
or P( A and B)  P ( A) P ( B )

Events A and B are independent when the
probability of one event, A, is not affected by
another event, B
Example

A series system of two components, C1 and C2. The
probability C1 fail is 0.1 and C2 fail is 0.2 and both of
them are independent.
C1


C2
The probability that the system fails is
P(C1 fail U C2 fail) =P(C1 fail) + P(C2 fail) P(C1,C2 fail)
= P(C1 fail) + P(C2 fail) P(C1 fail)xP(C2 fail)
Example

A paralel system of two components, C1 and C2. The
probability C1 fail is 0.1 and C2 fail is 0.2 and both of
them are independent.
C1
C2


The probability that the system fails is
P(C1 fail and C2 fail) =P(C1 fail).P(C2 fail)
=0.1x0.2 = 0.02
Total Probability


Let E and F be events. We may express E as
E = EF U EF’ , since both of them are
abviously mutually exclusive, we have that
P(E) = P(E|F)P(F) + P(E|F’)P(F’)
If F can be separated by F1 , F2 , …, F k and
each of them mutually exclusive then P(E) =
P(E|F1)P(F1) + …+ P(E|Fk)P(Fk )
Bayes’s Theorem
P  A | Bi  P  Bi 
P  Bi | A  
P  A | B1  P  B1       P  A | Bk  P  Bk 
P  Bi and A 

P  A
Same
Event
Adding up
the parts
of A in all
the B’s
Bayes’s Theorem
Using Contingency Table
Fifty percent of borrowers repaid their loans. Out of those
who repaid, 40% had a college degree. Ten percent of
those who defaulted had a college degree. What is the
probability that a randomly selected borrower who has a
college degree will repay the loan?
R = Repaid ; C = College
P  R   .50 P  C | R   .4
PR | C  ?
P  C | R   .10
Bayes’s Theorem
Using Contingency Table
(continued)
Repay
Repay
Total
College
.2
.05
.25
College
.3
.45
.75
Total
.5
.5
1.0
PR | C 
P C | R  P  R 
P C | R  P  R   P C | R  P  R 
.4 .5 

.2


 .8
.4 .5  .1.5  .25
Example

In answering a question on a multiple choice
test, a student either knowns the answer of
he guesses . Let p be the prob that she
knows the answer. There are m multiplechoice alternatives. What is the conditional
that a student knew the answer to a question
given that she answered it correctly ?
Solution

Let C and K denote respectively the event
that the student answers the question
correctly and the event that she actually
knows the answer. Now
P( K | C ) 

P (C|K ) P ( K )
P ( C | K ) P ( K )  P ( C | K ') P ( K ')
1 p
p  1/ m 1 p 
Example

A laboratory blood test is 95 percent effective
in detecting a certain disease when it is, in
fact present. However, the test also yields a “
false positive” result for 1 percent of the
healthy persons tested.
If 0.5 percent of the population actually has
the disease, what is the prob a person has
the disease given that his test result is
positive ?
Solution

Let D be the event that the tested person has
the disease, and E the event that his test
result is positive.
P( D | E ) 

P ( E|D ) P ( D )
P ( E | D ) P ( D )  P ( E | D ' ) P ( D ')
0.950.005
0.950.005 0.10.995
 0.323
Random Variable

Random Variable


Outcomes of an experiment expressed numerically
e.g.: Toss a die twice; count the number of times
the number 4 appears (0, 1 or 2 times)
Discrete Random Variable

Discrete random variable

Obtained by counting (1, 2, 3, etc.)

Usually a finite number of different values

e.g.: Toss a coin five times; count the number of
tails (0, 1, 2, 3, 4, or 5 times)
Discrete Probability
Distribution Example
Event: Toss two coins
Count the number of tails
Probability Distribution
Values
Probability
T
T
T
T
0
1/4 = .25
1
2/4 = .50
2
1/4 = .25
Example

Suppose we toss a coin having a prob p of
coming up heads, until the first head appears.
Letting N denote the number of flips
required, then assuming that the outcome of
successive flips are independent, N is a
random variable taking on one of the values
1,2,3,…with respective probabilities
Solution


P(N=1) = P(H) = p;
P(N=2) = P({T,H}) = (1-p)p ;
:
P(N=n) = P({T,…,T,H})= (1-p)n-1 p, n>=1
As a check, note that


P {N  n}   P{N  n}
 n 1
 n 1
 p  (1  p) n 1
n 1
 1
Discrete Probability Distribution

List of all possible [Xj , p(Xj) ] pairs

Xj = value of random variable

P(Xj) = probability associated with value

Mutually exclusive (nothing in common)

Collectively exhaustive (nothing left out)
0  P X j  1
P X  1
j
Summary Measures

Expected value (the mean)


Weighted average of the probability distribution
  E X    X jP X j 
j

e.g.: Toss 2 coins, count the number of tails,
compute expected value
   X jP X j 
j
  0  2.5  1.5   2 .25  1
Summary Measures

(continued)
Variance



Weight average squared deviation about the mean
  E  X        X j    P  X j 
2
2
2


e.g. Toss two coins, count number of tails,
compute variance
   X j    P X j 
2
2
  0  1 .25   1  1 .5    2  1 .25   .5
2
2
2
Covariance and its Application
N
 XY    X i  E  X   Yi  E Y  P  X iYi 
i 1
X : discrete random variable
X i : i th outcome of X
Y : discrete random variable
Yi : i th outcome of Y
P  X iYi  : probability of occurrence of the i
th
outcome of X and the i th outcome of Y
Correlation

The correlation coefficient of X and Y is

 XY
 XY
Computing the Mean for
Investment Returns
Return per $1,000 for two types of investments
P(XiYi)
Investment
Economic condition Dow Jones fund X Growth Stock Y
.2
Recession
-$100
-$200
.5
Stable Economy
+ 100
+ 50
.3
Expanding Economy
+ 250
+ 350
E  X    X   100.2  100.5   250.3  $105
E Y   Y   200.2   50.5   350.3  $90
Computing the Variance for
Investment Returns
P(XiYi)
Investment
Economic condition Dow Jones fund X Growth Stock Y
.2
Recession
-$100
-$200
.5
Stable Economy
+ 100
+ 50
.3
Expanding Economy
+ 250
+ 350
   100  105  .2   100  105  .5    250  105  .3 
2
2
X
2
2
 X  121.35
 14, 725
   200  90  .2    50  90  .5    350  90  .3
2
2
Y
 37,900
2
 Y  194.68
2
Computing the Covariance for
Investment Returns
P(XiYi)
Investment
Economic condition Dow Jones fund X Growth Stock Y
.2
Recession
-$100
-$200
.5
Stable Economy
+ 100
+ 50
.3
Expanding Economy
+ 250
+ 350
 XY   100  105 200  90 .2   100  105 50  90 .5
  250  105  350  90 .3  23,300
The Covariance of 23,000 indicates that the two investments are
positively related and will vary together in the same direction.
Correlation

The correlation coefficient of X and Y is


23, 300
121.35194.68
 0.986
If the value of X increase, then the value of Y
increase too.
Cumulative Distribution Function

The cumulative distribution function of a
random variable X is defined for any real x by

  f ( xi )
F ( x)  P( X  x)   xi
x
 f (t )dt

Example

Consider the
distribution of lifetimes ,
X (in months), of a
particular type of
component. We will
assume that the CDF
has the form
F ( x)  1  e
 ( 3x ) 2
;x  0

The median lifetime is
F (m)  0.5
 1 e
 

m
3
  m3 

m 2
3
2
 0. 5
 ln( 0.5)
  ln( 0.5)
1/ 2
m  2.498 months


It is desired to find the
time t such that 10% of
the component fail
before t. This is the 10th
percentile :
Thus if the components
are guaranteed for one
month, slightly more
than 10% will need to
be replaced
F ( x )  0.1
 1 e
 


x 2
3

x 2
3
 0.1
 ln( 0.9)
 x  3[ ln( 0.5)]
x  0.974 months
1/ 2
Important Discrete
Probability Distributions
Discrete Probability
Distributions
Binomial
Hypergeometric
Poisson
Binomial Probability Distribution

‘n’ identical trials


Two mutually exclusive outcomes on each
trials


e.g.: 15 tosses of a coin; ten light bulbs taken
from a warehouse
e.g.: Head or tail in each toss of a coin; defective
or not defective light bulb
Trials are independent

The outcome of one trial does not affect the
outcome of the other
Binomial Probability Distribution
(continued)

Constant probability for each trial


e.g.: Probability of getting a tail is the same each
time we toss the coin
Two sampling methods


Infinite population without replacement
Finite population with replacement
Binomial Probability
Distribution Function
n!
n X
X
P X  
p 1  p 
X ! n  X  !
P  X  : probability of X successes given n and p
X : number of "successes" in sample  X  0,1,
p : the probability of each "success"
Tails in 2 Tosses of Coin
n : sample size
X
0
P(X)
1/4 = .25
1
2/4 = .50
2
1/4 = .25
, n
Proof of the Probability

Note that, by the binomial theorem, the
probabilities sum to one, that is
 n x
n x
p( x)     p (1  p)

x 0
 x
n
 ( p  (1  p))
n
Binomial Distribution
Characteristics

Mean
  E  X   np
 E.g.   np  5 .1  .5


Variance and
Standard Deviation

 2  np 1  p 
  np 1  p 

P(X)
.6
.4
.2
0
n = 5 p = 0.1
X
0
1
2
3
E.g.
  np 1  p   5 .11  .1  .6708
4
5
Expectation
 n x
n x


E ( X )   x  p (1  p )
x 0
 x
n
n

x 1
 np
n!
( n  x )!( x 1)!
n

x 1
 np
n 1

k 0
 np
p (1  p )
x
n x
( n 1)!
( n  x )!( x 1)!
p
( n 1)!
( n 1 k )!( k )!
p (1  p )
x 1
k
(1  p )
n x
n  k 1
Variance
 n x
E ( X ( X  1))   x( x  1)  p (1  p ) n  x
x 0
 x
n
n
  ( n  x )!n(!x  2 )! p x (1  p) n  x
x2
 n(n  1) p
n
2

x2
 n(n  1) p 2
n2

k 0
 n(n  1) p 2
( n  2 )!
( n  x )!( x  2 )!
p x  2 (1  p) n  x
( n  2 )!
( n  2  k )!( k )!
p k (1  p) n  k  2
Binomial Distribution in PHStat


PHStat | probability & prob. Distributions |
binomial
Example in excel spreadsheet
Example

S uppose that an airplane engine will fall,
when in flight, with prob 1-p independently
from engine to engine; suppose that the
airplane will make a succesful flight if at least
50 percent of its engines remain operative.
For what values of p is a four-engine plane
preferable to a two-engine plane ?
Solution

The probaility that a four-engine plane makes
a successful flight is
 4 x
4 x
2
2
3
4




p
1

p

6
p
(
1

p
)

4
p
(
1

p
)

p

 x
x2  
4

Whereas the corresponding probability for a
two-engine plane is
2
 2 x
2 x
2



 x  p 1  p   2 p(1  p)  p
x 1  
Solution

Hence the four-engine is safer if
6 p (1  p)  4 p (1  p)  p  2 p(1  p) p
 3p  2  0
2
 p

2
3
4
2
2
3
Hence, the four-engine plane is safer when the
engine success probability is at least as large as 2/3 ,
whereas the two-engine plane is safer when this
probability falls below 2/3
Poisson Distribution

Poisson Process:

Discrete events in an “interval”





The probability of One Success
in an interval is stable
The probability of More than
One Success in this interval is 0
P( X  x |
- x
e 
x!
The probability of success is
independent from interval to
interval
e.g.: number of customers arriving in 15 minutes
e.g.: number of defects per case of light bulbs
Poisson Probability
Distribution Function

e 
P X  
X!
P  X  : probability of X "successes" given 
X
X : number of "successes" per unit
 : expected (average) number of "successes"
e : 2.71828 (base of natural logs)
e.g.: Find the probability of 4
customers arriving in 3 minutes
when the mean is 3.6.
e3.6 3.64
P X  
 .1912
4!
Poisson Distribution in PHStat


PHStat | probability & prob. Distributions |
Poisson
Example in excel spreadsheet
Poisson Distribution
Characteristics

Mean

= 0.5
P(X)
  EX   
N
  XiP  Xi 
.6
.4
.2
0
X
0
1
i 1

Standard Deviation
and Variance

 
2
 
2
3
4
5
= 6
P(X)
.6
.4
.2
0
X
0
2
4
6
8
10
Approximate a binomial to poisson

An important property of the poisson random
variable is that it may be used to
approximate a binomial random variabel when
the binomial parameter n is large and p is
small. To see this, suppose that X is a
binomial r.v. with parameters (n,p), and let µ
= np. Then
Proof
P( X  i) 

  1  
i

n!
( n i )!i! n
n ( n 1)...( n i 1)  i 1  / n n
i! (1  / n ) i
ni
e
1   / n
n
 n i
n
  i
i!

 e ; (1   / n)  1;
i
n ( n 1)...( n i 1)
n
i
1
Expectation

E( X )  
x
xe 
x!
x 0
 e

x


x 1

 e e



 
x 1
 x1
( x 1)!
e   x1
( x 1)!
Variance

E ( X ( X  1))  
x 0
    1e
x x
x ( x 1) e 
x!



x2
    1e e
    1
 

    1
 x 2
( x  2 )!
x2
e   x2
( x  2 )!
Hypergeometric Distribution

“n” trials in a sample taken from a finite
population of size N

Sample taken without replacement

Trials are dependent

Concerned with finding the probability of “X”
successes in the sample where there are “A”
successes in the population
Hypergeometric Distribution
Function
 A   N  A
 

X
n

X

P X    
N
 
n 
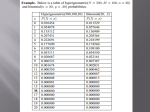
E.g. 3 Light bulbs were
selected from 10. Of the 10
there were 4 defective. What
is the probability that 2 of the
3 selected are defective?
P  X  : probability that X successes given n, N , and A
 4  6 
  
2 1 

P  2 
 .30
10 
A : number of "successes" in population
 
3 
X : number of "successes" in sample
n : sample size
N : population size
X
 0,1, 2,
, n
Hypergeometric Distribution
Characteristics

Mean


A
  EX   n
N
Variance and Standard Deviation

nA  N  A N  n
2
 
N2
N 1
nA  N  A N  n

2
N
N 1
Finite
Population
Correction
Factor
Hypergeometric Distribution in
PHStat


PHStat | probability & prob. Distributions |
Hypergeometric …
Example in excel spreadsheet
Expectation
E( X ) 



 
1
2 
1
2

 ( x   ) 2 / 2 2
xe



1
2 
0  
( x   )e


e

dx
 ( x   ) 2 / 2 2
 ( x   ) 2 / 2 2
dx
d x    
Variance
EX    
2





 
1
2 

2

2

2
(

2
x 2

) e
 ( x ) 2 / 2
2  y2 / 2
y e
dy
d
 
x

Jointly Distributed Random Variables


The joint probability mass function of X and Y
is p(x,y)=P(X=x,Y=y)
The probability mass function of X
  p ( x, y )

p( x)    y
 f  x, y dy
 

The probability mass function of Y
  p ( x, y )
 x
p( y )   
f  x, y dx


Expectation
E( X  Y )  


 x  y  f ( x, y)dxdy
 






  x  f ( x, y)dy dx   y  f ( x, y)dx dy
  
  







  xf ( x)dx   yf ( y )dy
 E ( X )  E (Y )
E ( X 1  ...  X n )  E ( X 1 )  ...  E ( X n )
Example

As another example of the usefulness of
equation above, let us use it to obtain the
expectation of a binomial r.v.
1, succes
Xi  
; E ( X i )  p ; V ( X i )  pq
0, failed
X
 X 1  ...  X n
E ( X )  E ( X 1 )  ...  E ( X n )  np
V ( X )  V ( X 1 )  ...  V ( X n )  npq
Example

At a party N men throw their hats into the
center of a room. The hats are mixed up and
each man randomly selects one. Find the
expected number of men that select their own
hats
Solution

Letting X denote the number of men that
select their own hats, we can best compute
E(X) by noting that X = X1+…+XN ; where Xi
is indicator function if the ith man select his
own hat. So P(Xi = 1) = 1/N. And so E(Xi) =
1/N. Hence We obtain that E(X) = 1. So, no
matter how many people are at the party, on
the average exactly one of the men will select
his own hat.
Independent R.V

X and Y are
independent if
E ( XY )  

 xyf ( x, y)dxdy
   xyf ( x) f ( y)dxdy
  xf ( x)dx  yf ( y)dy
 

 p ( x, y )  p ( x ) p ( y )

 f ( x, y )  f ( x ) f ( y )


 




 E ( X ) E (Y )
Covariance and Variance of Sums of
Random Variables



The covariance of any two random variables X
and Y, denoted by Cov(X,Y), is defined by
Cov(X,Y)
= E[(X-E[X])(Y-E[Y])]
= E(XY)-E(X)E(Y)
If X and Y are independent Cov(X,Y) = 0
Properties of Covariance
Cov(x,X) = Var(X)
 Cov(cX,Y) = c Cov(X,Y)
 Cov(X,Y+Z)= E[X(Y+Z)]-E[X]E[Y+Z]
= E[XY]-E[X]E[Y] + E[XZ]-E[X]E[Z]
= (Cov(X,Y) + Cov(X,Z)
The last property easily generalizes to give

Cov X i ,Y j    Cov(X i , Y j )
Variance of Sum Variabel
n
 n

 n

Var   X i   Cov  X i ,  X i 
j 1
 i 1 
 i 1

n
n
  Cov( X i , X j )
i 1 j 1
n
n
n
  Cov( X i , X i )   Cov( X i , X j )
i 1
n
i 1 j  i
n
n
  V ( X i )  2 Cov( X i , X j )
i 1
i 1 j i
Proposition

Suppose that X1,…,Xn are independent and
identically distributed with expected value µ
and variance σ2. Then
Cov( X , X i  X )  Cov( X , X i )  Cov( X , X )
 1n Cov( X i   X i , X j )  Var ( X )
j i
 1n Cov( X i , X i )  1n Cov( X i   X j )  Var ( X )
j i

2
n
0
2
n
Example


Sums of independent Poisson Random
Variables : Let A and Y be independent
Poisson random variables wirh respective
means λ1 and λ2 . Calculate the distribution of
X + Y.
Solution : Since the event {X+Y = n} may be
written as the union of the disjoint events
{X=k,Y=n-k}, 0≤k≤n, we have
n
P ( X  Y  n)   P{ X  k , Y  n  k }
k 0
n
  P{ X  k }P{Y  n  k }
k 0
n
e
k 0
e

 1 1k
k!
 1 2 
n!
e  12 
n!
e
 2
n2k
( n  k )!
n

k 0
n!
k !( n  k )!
1  2 
1k n2 k
n