* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Slide 1
Fundamental theorem of algebra wikipedia , lookup
Linear algebra wikipedia , lookup
Complexification (Lie group) wikipedia , lookup
Universal enveloping algebra wikipedia , lookup
Boolean algebras canonically defined wikipedia , lookup
Exterior algebra wikipedia , lookup
Geometric algebra wikipedia , lookup
Heyting algebra wikipedia , lookup
Laws of Form wikipedia , lookup
Homological algebra wikipedia , lookup
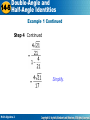
Double-Angle Double-Angleand and 14-5Half-Angle 14-5 Half-AngleIdentities Identities Warm Up Lesson Presentation Lesson Quiz Holt Algebra Holt Algebra 22 Double-Angle and 14-5 Half-Angle Identities Warm Up Find tan θ for 0 ≤ θ ≤ 90°, if 1. 2. 3. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Objective Evaluate and simplify expressions by using double-angle and half-angle identities. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities You can use sum identities to derive the double-angle identities. sin 2θ = sin(θ + θ) = sinθ cosθ + cosθ sinθ = 2 sinθ cosθ Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities You can derive the double-angle identities for cosine and tangent in the same way. There are three forms of the identity for cos 2θ, which are derived by using sin2θ + cos2θ = 1. It is common to rewrite expressions as functions of θ only. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Example 1: Evaluating Expressions with Double-Angle Identities Find sin2θ and tan2θ if sinθ = and 0°<θ<90°. Step 1 Find cosθ to evaluate sin2θ = 2sinθcosθ. Method 1 Use the reference angle. In Ql, 0° < θ < 90°, and sinθ = x2 + 22 = 52 Use the Pythagorean Theorem. Solve for x. r=5 θ x Holt Algebra 2 y=2 Double-Angle and 14-5 Half-Angle Identities Example 1 Continued Method 2 Solve cos2θ = 1 – sin2θ. cos2θ = 1 – sin2θ cosθ = Substitute Simplify. Holt Algebra 2 for cosθ. Double-Angle and 14-5 Half-Angle Identities Example 1 Continued Step 2 Find sin2θ. sin2θ = 2sinθcosθ Apply the identity for sin2θ. Substitute for cosθ. Simplify. Holt Algebra 2 for sinθ and Double-Angle and 14-5 Half-Angle Identities Example 1 Continued Step 3 Find tanθ to evaluate tan2θ = . Apply the tangent ratio identity. Substitute for cosθ. Simplify. Holt Algebra 2 for sinθ and Double-Angle and 14-5 Half-Angle Identities Example 1 Continued Step 4 Find tan 2θ. Apply the identity for tan2θ. Substitute Holt Algebra 2 for tan θ. Double-Angle and 14-5 Half-Angle Identities Example 1 Continued Step 4 Continued Simplify. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Caution! The signs of x and y depend on the quadrant for angle θ. sin cos Ql + + Qll + – Qlll – – QlV – + Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 1 Find tan2θ and cos2θ if cosθ = 270°<θ<360°. and Step 1 Find tanθ to evaluate tan2θ = . Method 1 Use the reference angle. In QlV, 270° < θ < 360°, and cosθ = 12 + y2 = 32 Use the Pythagorean Theorem. x=1 Solve for y. θ r=3 Holt Algebra 2 y= –2√ 2 Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 1 Continued Step 2 Find tan2θ. tan2θ = Apply the identity for tan2θ. Substitute –2 Simplify. Holt Algebra 2 for tanθ. Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 1 Continued Step 3 Find cos2θ. cos2θ = 2cos2θ – 1 Apply the identity for cos2θ. Substitute Simplify. Holt Algebra 2 for cosθ. Double-Angle and 14-5 Half-Angle Identities You can use double-angle identities to prove trigonometric identities. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Example 2A: Proving identities with Double-Angle Identities Prove each identity. sin 2θ = 2tanθ – 2tanθ sin2θ Choose the right-hand side to modify. = 2tanθ (1– sin2θ) = 2tanθ cos2θ = 2(tanθcosθ)cosθ = 2sinθcosθ = sin2θ Holt Algebra 2 Factor 2tanθ. Rewrite using 1 –sin2θ = cos2θ. Regroup. Rewrite using tanθcosθ = sinθ. Apply the identity for sin2θ. Double-Angle and 14-5 Half-Angle Identities Example 2B: Proving identities with Double-Angle Identities cos2θ = (2 – sec2θ)(1 – sin2θ) cos2θ = (2 – sec2θ)(1 – sin2θ) = (2 – sec2θ)(cos2θ) Choose the right-hand side to modify. Rewrite using 1 – sin2θ = cos2θ. = 2cos2θ – 1 Expand and simplify. = cos2θ Apply the identity for cos2θ. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Helpful Hint Choose to modify either the left side or the right side of an identity. Do not work on both sides at once. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 2a Prove each identity. cos4θ – sin4θ = cos2θ (cos2θ – sin2θ)(cos2θ + sin2θ) = (1)(cos2θ) = Factor the left side. Rewrite using 1 = cos2θ + sin2θ and cos2θ = cos2θ – sin2θ. cos2θ = cos2θ Simplify. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 2b Prove each identity. Rewrite tan θ ratio identity and Pythagorean identity. Reciprocal sec θ identity and simplify fraction. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 2b Continued Prove each identity. Simplify. Double angle identity. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities You can use double-angle identities for cosine to derive the half-angle identities by substituting for θ. For example, cos2θ = 2 cos2θ – 1 can be rewritten as cosθ = 2 cos2 – 1. Then solve for cos Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Half-angle identities are useful in calculating exact values for trigonometric expressions. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Example 3A: Evaluating Expressions with Half-Angle Identities Use half-angle identities to find the exact value of cos 15°. Positive in Ql. Cos 30° = Simplify. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Example 3A Continued Check Use your calculator. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Example 3B: Evaluating Expressions with Half-Angle Identities Use half-angle identities to find the exact value of . Negative in Qll. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Example 3B Continued Simplify. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Example 3B Continued Check Use your calculator. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 3a Use half-angle identities to find the exact value of tan 75°. tan (150°) Positive in Ql. Simplify. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 3a Continued Check Use your calculator. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 3b Use half-angle identities to find the exact value of . Negative in Qll. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 3b Continued Simplify. Check Use your calculator. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Example 4: Using the Pythagorean Theorem with HalfAngle Identities Find cos and tan if tan θ = and 0<θ< Step 1 Find cos θ to evaluate the half-angle identities. Use the reference angle. In Ql, 0 < θ < 242 + 72 = x2 and tanθ = Pythagorean Theorem. Solve for the missing side x. Thus, cosθ = Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Example 4 Continued Step 2 Evaluate cos x θ Choose + for cos where 0 < θ < Evaluate. Holt Algebra 2 24 7 Double-Angle and 14-5 Half-Angle Identities Example 4 Continued Simplify. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Example 4 Continued Step 3 Evaluate tan Choose + for tan 0<θ< Evaluate. Holt Algebra 2 where Double-Angle and 14-5 Half-Angle Identities Example 4 Continued Simplify. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 4 Find sin and cos if tan θ = and 0 < θ < 90. Step 1 Find cos θ to evaluate the half-angle identities. Use the reference angle. In Ql, 0 < θ < 42 + 32 = r and tanθ = 2 Pythagorean Theorem. r= Thus, cosθ = Holt Algebra 2 . Solve for the missing side r. Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 4 Continued Step 2 Evaluate cos r θ Choose + for cos where 0 < θ < Evaluate. Simplify. Holt Algebra 2 3 4 Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 4 Continued Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 4 Continued Step 3 Evaluate sin Choose + for sin < 90°. Evaluate. Holt Algebra 2 where 0 < θ Double-Angle and 14-5 Half-Angle Identities Check It Out! Example 4 Continued Simplify. Holt Algebra 2 Double-Angle and 14-5 Half-Angle Identities Lesson Quiz: Part I 1. Find cos and cos 2θ if sin θ = 2. Prove the following identity: Holt Algebra 2 and 0 < θ < Double-Angle and 14-5 Half-Angle Identities Lesson Quiz: Part II 3. Find the exact value of cos 22.5°. Holt Algebra 2