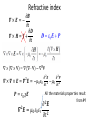Download Quantum Dots in Photonic Structures

Quantum Dots in Photonic Structures
Lecture 3:
Solution of Maxwell equations in a periodic dielectric
Jan Suffczyński
Wednesdays, 17.00, SDT
Projekt Fizyka Plus nr POKL.04.01.02-00-034/11 współfinansowany przez Unię Europejską ze środków Europejskiego
Funduszu Społecznego w ramach Programu Operacyjnego Kapitał Ludzki
Zasady zaliczenia przedmiotu
• Egzamin ustny na koniec semestru:
dwa pytania ze znanego uprzednio zestawu pytań
Literatura
• Photonic crystals: molding the flow of light, John D.
Joannopoulos, wyd. II, Princeton University Press, 2008
• Controlling spontaneous emission dynamics in semiconductor
microcavities: an experimental approach, Bruno Gayral, Ann.
Phys. Fr. 26 No 2, EDP Sciences, 2001
• Cavity quantum electrodynamics, S. Haroche, D. Kleppner,
Phys. Today 42, 24 (1989).
• Cavity quantum electrodynamics, S. Haroche, J-M. Raimond,
Scientific Amarican (April 1993).
• Microcavities, A. V. Kavokin, J.J. Baumberg, G. Malpuech,
F. P. Laussy, Oxford Press, 2007
Reminder
• Quality factor: a measure of the rate at which
optical energy decays from the cavity
(absorption, scattering, leakage due to
imperfect mirrors)
Lifetime of the photon
Q  c / 
within the cavity:

τ = 1/Γ= Q/ωc
c
Reminder: Fermi’s Golden Rule
• Spontaneous emission rate is not an inherent property of the emitter
• Sponteanous emission rate proportional to:
Dipol moment
Density of
of the emitter Electric field intensity
photon states
at emitter position
at emitter wavelength
Γ ∝ 𝜌(𝜔)·|𝐝·𝐄 𝐫emitter
2
|
Reminder: Fermi’s Golden Rule
• Spontaneous emission rate is not an inherent property of the emitter
• Sponteanous emission rate proportional to:
Dipol moment
Density of
of the emitter Electric field intensity
photon states
at emitter position
at emitter wavelength
Γ ∝ 𝜌(𝜔)·|𝐝·𝐄 𝐫emitter
mirror
Spontaneous emission inhibited
2
|
mirror
Spontaneous emission enhanced
Weak vs strong coupling
Out of
the cavity
Weak vs strong coupling
Out of
the cavity
Plan for today
1. Refractive
index of the
matter
2. Onedimensional
photonic crystal
(Bragg Mirror)
3. Twodimensional
photonic crystal
EM wave interacting with dielectric medium
In linear, homogeneous, and
isotropic media polarization
P linearly proportional to E:
𝑷 = 𝜀0 𝜒𝑬
 - a scalar constant called the
“electric susceptibility”
𝑫 = 𝜀0 𝑬 + 𝑷
Define relative dielectric constant as:
𝑟 = 1 + 𝜒
𝑫 = 𝜀0 𝜀𝑟 𝑬
Note:
In anisotropic media P and E are not necessarily parallel:
In nonlinear media:
Refractive index
𝜕𝑩
𝜵×𝑬=−
𝜕𝑡
𝜕𝑫
𝜵×𝑯=𝑱+
𝜕𝑡
2
𝜵×𝜵×𝑬=𝜵 𝑬=
𝑷 = 𝜀0 𝜒𝑬
𝜕2 𝑬
−𝜇0 𝜀0 2
𝜕𝑡
𝜕2 𝑷
−𝜇0 2
𝜕𝑡
All the materials properties result
from P!
2
𝜕 𝑬
𝜵 𝑬 = 𝜇0 𝜀0 𝜀𝑟 2
𝜕𝑡
2
Refractive index - dispersion
𝜵2 𝑬
=
𝜕2 𝑬
𝜇0 𝜀0 𝜀𝑟 2
𝜕𝑡
=
𝑛2 𝜕2 𝑬
𝑐 2 𝜕𝑡 2
The light slows down in the medium!
𝑐 𝜔
(phase speed < c)
𝑣=
𝑛
=
𝑘
Wave equation:
Refractive index: 𝑛 =
𝜀𝑟
Refractive index
Material with an index
of refraction n
The light slows down inside the
material, therefore its wavelength
becomes shorter and its phase gets
shifted
E y  A sin(nz / 0  t )
In
Out
After: András Szilágyi
• As light travels from one
medium to another:
– Both the wave speed and the
wavelength do change
– The wavefronts do not pile
up, nor are created or
destroyed at the boundary,
so, frequency does not
change
Refractive index
Refractive index - dispersion
𝜵2 𝑬
=
𝜕2 𝑬
𝜇0 𝜀0 𝜀𝑟 2
𝜕𝑡
=
𝑛2 𝜕2 𝑬
𝑐 2 𝜕𝑡 2
The light slows down in the medium!
𝑐 𝜔
(phase speed < c)
𝑣=
Wave equation:
Refractive index: 𝑛 =
=
𝑛 𝑘
𝑛 = 𝑛 (when no absorption)
The dependence of n on λ is called dispersion
• n usually decreases
with increasing
wavelength
• violet light refracts
more than red light
when passing from
air into a material
𝜀𝑟
Refractive index
In the case of absorbing medium:
Complex dielectric function 𝜀𝑟 (𝜔)
𝜀𝑟 (𝜔) = 𝑛 𝜔 + 𝑖 ∙ 𝜅(𝜔)
𝑬 𝑧, 𝑡 = Re 𝑬0
𝑒 𝑖 𝑘𝑛𝑧−𝜔𝑡
allows simultaneous
description of refraction
and absorption
2𝜋
= Re
𝑖
(𝑛+𝑖𝜅)𝑧−𝜔𝑡
𝑬0 𝑒 𝜆0
2𝜋
2𝜋
=𝑒
− 𝜆 𝜅𝑧
Exponential decay
0
Re
𝑖
𝑛𝑧−𝜔𝑡
𝑬0 𝑒 𝜆0
Propagation
with phase speed c/n
Photonic crystals - introductory example
1. Bragg scattering
Regardless of how small the reflectivity r is from an individual
scatterer, the total reflection R from a semi infinite structure:
Complete reflection when:
 Propagation of the light in crystal inhibited when Bragg condition satisfied
 Origin of the photonic bang gap
Fabry–Pérot interferometer
I0
Fabry–Pérot interferometer
I0
Fresnel:
Fabry–Pérot interferometer
The reflectance of the etalon Retalon:
The transmission of the etalon Tetalon:
Maxima of the transmission for multiples of π
Photonic crystals
Photonic crystal:
Periodic arrangement of dielectric (or metallic…)
objects
( periodic refractive index contrast!)
• The period comparable to the wavelength of
light in the material.
1D photonic crystal: a Bragg mirror
Photonic crystals
1887
1987
1-D
2-D
periodic in
one direction
periodic in
two directions
3-D
periodic in
three directions
Media with periodic refractive indeces
giving rise to photonic band gaps: “optical insulators”
Photonic crystals
Media with periodic refractive indeces
can trap light in cavities
3D Pho to nic C rysta l with De fe c ts
and act as waveguides
Media with periodic refractive indeces
giving rise to photonic band gaps: “optical insulators”
1D photonic crystal: a Bragg mirror
Quaterwave stack condition
d1
d2
n1
n2
d1n1=d2n2=Br/4
d1 kn1=d2 kn2=
Br/4*(2π/Br) π/2
 destructive interference
of the reflected wave
with the incident wave!
Example
GaaS/AlAs Bragg mirror:
1D photonic crystal: a Bragg mirror
Distributed Bragg
Reflector in
Transfer Matrix Method
formalism
Blackboard calculation
(for a reference see for example C. B. Fu, C. S.
Yang, M. C. Kuo, Y. J. Lai, J. Lee, J. L. Shen, W. C.
Chou, and S. Jeng, High Reflectance ZnTe/ZnSe
Distributed Bragg Reector at 570 nm, CHINESE
JOURNAL OF PHYSICS 41, 535 (2003).
(mind the error in Equation 14: i = 1  i = 2)
Summary
• Complex refractive index - describes refraction
and absorption
• Photonic crystals are artificial media with a
periodic index contrast (period comparable to
the wavelength of light in the material)
• Bragg mirror calculated within Transfer Matrix
formalism