Download Factoring Trinomials 2

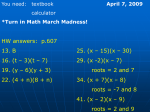
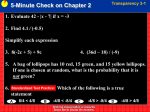
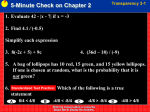
Factoring Polynomials and
Solving Equations
by Factoring
Copyright © Cengage Learning. All rights reserved.
5
Section
5.4
Factoring Trinomials with a
Leading Coefficient Other Than 1
Copyright © Cengage Learning. All rights reserved.
Objectives
1 Factor a trinomial of the form ax2 + bx + c
using trial and error.
2 Factor a trinomial of the form ax2 + bx + c by
grouping (ac method).
3 Factor a polynomial involving a perfect-square
trinomial.
3
Factoring Trinomials with a Leading Coefficient Other Than 1
We saw how to factor trinomials whose leading coefficients
are 1. We now show how to factor trinomials whose leading
coefficients are other than 1.
4
1. Factor a trinomial of the form
ax2 + bx + c using trial and error
5
Factor a trinomial of the form ax2 + bx + c using trial and error
We must consider more combinations of factors when we
factor trinomials with leading coefficients other than 1.
Factoring General Trinomials Using Trial and Error
1. Write the trinomial in descending powers of one variable.
2. Factor out any GCF (including –1 if that is necessary to
make the coefficient of the first term positive).
6
Factor a trinomial of the form ax2 + bx + c using trial and error
3. If the sign of the third term is +, the signs between the
terms of the binomial factors are the same as the sign of
the middle term. If the sign of the third term is –, the
signs between the terms of the binomial factors are
opposites.
4. Try combinations of first terms and last terms until you
find one that works, or until you exhaust all the
possibilities. If no combination works, the trinomial is
prime.
5. Check the factorization by multiplication.
7
Example
Factor: 2x2y – 8x3 + 3xy2.
Solution:
Step 1: Write the trinomial in descending powers of x.
–8x3 + 2x2y + 3xy2
Step 2: Factor out the negative of the GCF, which is –x.
–8x3 + 2x2y + 3xy2 = –x(8x2 – 2xy – 3y2)
Step 3: Because the sign of the third term of the trinomial
factor is –, the signs within its binomial factors will
be opposites.
8
Example – Solution
cont’d
Step 4: Find the binomial factors of the trinomial.
–8x3 + 2x2y + 3xy2 = –x(8x2 – 2xy – 3y2)
= –x(2x + y)(4x – 3y)
Step 5: Check by multiplication.
–x(2x + y)(4x – 3y) = –x(8x2 – 6xy + 4xy – 3y2)
= –x(8x2 – 2xy – 3y2)
= –8x3 + 2x2y + 3xy2
= 2x2y – 8x3 + 3xy2
9
2. Factor a trinomial of the form
ax2 + bx + c by grouping (ac method)
10
Factor a trinomial of the form ax2 + bx + c by grouping (ac method)
Another way to factor trinomials of the form ax2 + bx + c
uses the grouping (ac method).
For example, to factor 6x2 – 17x + 5 (Example 2) by
grouping, we note that a = 6, b = –17, and c = 5 and
proceed as follows:
1. Determine the product ac: 6(+5) = 30. This is the key
number.
2. Find two factors of the key number 30 whose sum is
–17. Two such factors are –15 and –2.
–15(–2) = 30
and
–15 + (–2) = –17
11
Factor a trinomial of the form ax2 + bx + c by grouping (ac method)
3. Use –15 and –2 as coefficients of two terms to be placed
between 6x2 and 5 to replace –17x.
6x2 – 17x + 5 = 6x2 – 15x – 2x + 5
4. Factor the right side of the previous equation by
grouping.
6x2 – 15x – 2x + 5 = 3x(2x – 5) – 1(2x – 5)
= (2x – 5)(3x – 1)
Factor the GCF, 3x,
from (6x2 – 15x) and
–1 from (–2x + 5).
Factor out the GCF,
(2x – 5).
Verify this factorization by multiplication.
12
Example
Factor 4y2 + 12y + 5 by grouping.
Solution:
To factor this trinomial by grouping, we note that it is written
in the form ay2 + by + c, with a = 4, b = 12, and c = 5. Since
a = 4 and c = 5, we have ac = 20.
We now find two factors of 20 whose sum is 12. Two such
factors are 10 and 2.
13
Example – Solution
cont’d
We use these factors as coefficients of two terms to be
placed between 4y2 and 5 to replace +12y.
4y2 + 12y + 5 = 4y2 + 10y + 2y + 5
Finally, we factor the right side of the previous equation by
grouping.
Factor the GCF, 2y,
4y2 + 10y + 2y + 5 = 2y(2y + 5) + (2y + 5)
from (4y2 + 10y).
= 2y(2y + 5) + 1  (2y + 5)
= (2y + 5)(2y + 1)
Check by multiplication.
Write the coefficient
of 1.
Factor out the GCF,
(2y + 5).
14
3.
Factor a polynomial involving a
perfect-square trinomial
15
Example
Factor: 4x2 – 20x + 25.
Solution:
4x2 – 20x + 25 is a perfect-square trinomial, because
• The first term is 4x2 is the square of 2x: (2x)2 = 4x2.
• The last term 25 is the square of 5: 52 = 25.
• The middle term –20x is the negative of twice the product
of 2x and 5.
16
Example – Solution
cont’d
Thus,
4x2 – 20x + 25 = (2x)2 – 2(2x)(5) + 52
= (2x – 5)2
Check by multiplication.
17