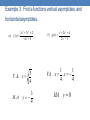Download U2Day6

Bellwork
1. Find a polynomial function with integer coefficients that has the given zeros.
4, 3i
2. Find all zeros of the function, write the polynomial as a product of linear factors.
f ( x)  x 4  8x3  17 x 2  8x  16
Last Nights Homework
•
41. x 3  x 2  25 x  25
43. x 3  10 x 2  33x  34
45.
x 4  37 x 2  36
53.
-3/2, ±5i
55.
-3, 5, ±2i
65. No, Setting h = 64 and solving the resulting equation yields imaginary roots,
2.6 Rational Functions and Asymptotes
-How to find domains of rational functions?
-How to find horizontal and vertical asymptotes of
graphs of rational functions?
Rational Functions and Asymptotes
• A rational function can be written in the form
N ( x)
f ( x) 
D( x)
Where N(x) and D(x) are polynomials
The most basic rational function
Domain: (-∞,∞)
Horizontal Asymptote: x = 0
Vertical Asymptote: y = 0
• The line x = a is a vertical asymptote of the graph of f if
f(x)→∞ or f(x)→-∞ as x→a, either from the right or the left.
• The line y = b is a horizontal asymptote of the graph of f
if f(x)→b as x→∞ or x→-∞.
Vertical Asymptotes
• Let f be the rational function
N ( x)
f ( x) 
D( x)
Where N(x) and D(x) have no common factors.
The graph of f has vertical asymptotes at the zeros of D(x).
Example 1: Find the Vertical Asymptotes.
a)
x2  4
f ( x) 
x2
Hole at
x = -2
No VA
x 3
b) g ( x )  2
x  3x
VA at
x = 0,
Hole at x = 3
c) w( x) 
2x  8
x 2  9 x  20
VA at x = 5
Hole at x = 4
Horizontal Asymptotes
n
ax ...
f ( x)  m
bx ...
• The graph f has at most one horizontal asymptote
determined by looking at the exponents of the
numerator and the denominator.
• If n < m, then y = 0 is the H.A.
• If n = m, then y = a/b is the H.A.
• If n > m, then there is no H.A.
Example 2: Find the H.A. of the following functions.
a)
2x
f ( x)  2
3x  1
Bigger exponent in D(x).
H.A. y = 0
2x2
b) g ( x )  2
3x  1
Same exponent in N(x)
and D(x). H.A. y = 2/3
2 x3
c ) h( x )  2
3x  1
Bigger exponent in
N(x). No H.A.
Example 3: Find a functions vertical asymptotes, and
horizontal asymptotes.
a)
3x 3  7 x 2  2
f ( x) 
 4 x3  5
5
3
V . A. x 
4
H .A
3
y
4
x3  2 x 2  4
b) g ( x ) 
2x2 1
1
1
VA x  , x  
4
4
HA
y0
Tonight’s Homework
• Pg 195 #7-19. #40, 41