Download y - Images

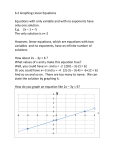
1. Interpret graphs.
2. Write a solution as an ordered pair.
3. Decide whether a given ordered pair is
a solution of a given equation.
4. Complete ordered pairs for a given
equation.
5. Complete a table of values.
6. Plot ordered pairs.
Interpret Graphs.
A linear equation in two variables is an equation that can be
written in the form
Ax  By  C ,
where A, B, and C are real numbers and A and B are not both 0.
Some examples of linear equations in two variables in this
form, called standard form, are
equations
3 x  4 y  9, x  y  0, and x  2 y  8. Linear
in two variables
Other linear equations in two variables, such as
y  4x  5
3 x  7  2 y,
and
are not written in standard form, but could be. We discuss the
forms of linear equations in more detail in Section 10.4.
10.1.2 Write a solution as an ordered pair.
A solution of a linear equation in two variables requires two
numbers, one for each variable. For example, a true statement
results when we replace x with 2 and y with 13 in the equation
y  4 x  5, since 13  4  2  5.
The pair of numbers x = 2 and y = 13 gives a solution of the
equation y  4 x  5. The phrase “x = 2 and y = 13” is abbreviated
y-value
x-value
 2,13
The x-value is always given first. A pair of numbers such as
(2,13) is called an ordered pair, since the order in which the
numbers are written is important.
The ordered pairs (2,13) and (13,2) are not the same. The
second pair indicates that x = 13 and y = 2. For ordered pairs to
be equal, their x-coordinates must be equal and their y-coordinates
must be equal.
10.1.3 Decide whether a given ordered pair is
a solution of a given equation.
We substitute the x- and y-values of an ordered pair into a
linear equation in two variables to see whether the ordered pair
is a solution. An ordered pair that is a solution of an equation is
said to satisify the equation.
Infinite numbers of ordered pairs can satisfy a linear equation in two
variables.
When listing ordered pairs, be sure to always list the x-value first.
Problem:
Deciding Whether Ordered Pairs
Are Solutions of an Equation
Decide (yes or no) whether each ordered pair is a
solution of the equation 5 x  2 y  20.
 2, 5 Solution: 5  2  2  5  20
10   10  20
0  20
 4, 20
No
5  4  2  20  20
20  40  20
20  20
Yes
10.1.4 Complete ordered pairs for a given equation.
Complete each ordered pair for the equation y  2 x  9.
 2, 
 , 7 
Solution: y  2  2  9
y  49
y  5
7  9  2x  9  9
16 2x

2
2
x 8
 2, 5
8,7 
10.1.5 Completing Tables of Value
Complete the table of values for the equation
2 x  3 y  12. Then write the results as ordered pairs.
Solution:
4
6
2
3
2
2  0  3 y  12
3 y 12

3 3
 0, 4 
y  4
2  3  3 y  12
6  3 y  6  12  6
3 y 6

 3, 2  3 3
y  2
2x  3  0  12
2 x 12

2
2
x6
 6, 0 
2x  3  3  12
2x  9  9  12  9
2x 3

2
2
x
3
2
3

,

3


2


10.1.6 Plot ordered pairs.
Every linear in two variables equation has an infinite number
of ordered pairs as solutions. Each choice of a number for one
variable leads to a particular real number for the other variable.
To graph these solutions, represented as ordered pairs (x,y),
we need two number lines, one for each variable. The two
number lines are drawn as shown
below. The horizontal number line is
called the x-axis and the vertical line
is called the y-axis. Together, these
axes form a rectangular coordinate
system, also called the Cartesian
coordinate system.
Plot ordered pairs. (cont’d)
The coordinate system is divided into four regions, called
quadrants. These quadrants are numbered counterclockwise,
starting with the one in the top right quadrant.
Points on the axes themselves are not in any quadrant.
The point at which the x-axis and y-axis meet is called the
origin, labeled 0 on the previous diagram. This is the point
corresponding to (0, 0).
The x-axis and y-axis determine a plane— a flat surface
illustrated by a sheet of paper. By referring to the two axes, we
can associate every point in the plane with an ordered pair. The
numbers in the ordered pair are called the coordinates of the
point.
In a plane, both numbers in the ordered pair are needed to
locate a point. The ordered pair is a name for the point.
Plot ordered pairs. (cont’d)
For example, locate the point associated with the ordered pair
(2,3) by starting at the origin.
Since the x-coordinate is 2, go 2 units to the right along the
x-axis.
Since the y-coordinate is 3, turn
and go up 3 units on a line parallel to
the y-axis.
The point (2,3) is plotted in the
figure to the right. From now on
the point with x-coordinate 2 and
y-coordinate 3 will be referred to as
point (2,3).
EXAMPLE:
Plotting
Ordered Pairs
Plot the given points in a coordinate system:
 3,5 ,  2,6 ,  4,0 ,  5, 2 , 5, 2 ,  0, 6 .
EXAMPLE 7:
Completing Ordered Pairs to
Estimate the Number of Twin
Births
Complete the table of ordered pairs for the equation,
y  3.563x  7007.7., where x = year and y = number
of twin births in thousands. Round answers to the
nearest whole number. Interpret the results for 2002.
115
122
125
Solution:
There were about 125
thousand twin births in
the U.S. in 2002.
y  3.563 1999  7007.7
y  7122.4  7007.7
y  115
y  3.563  2001  7007.7
y  7.129.6  7007.7
y  122
y  3.563 2002  7007.7
y  7133.1  7007.7
y  125
Plot ordered pairs. (cont’d)
The ordered pairs of twin births in the U.S. for 1998, 2000,
and 2003 are graphed to the right. This graph of ordered pairs
of data is called a scatter diagram.
Notice how the how the axes are labeled:
x represents the year, and y represents
the number of twin births in thousands.
A scatter diagram enables us to tell whether two quantities
are related to each other. These plotted points could be
connected to form a straight line, so the variables x (years) and
y (number of births have a linear relationship.
Plot ordered pairs. (cont’d)
Think of ordered pairs as representing an input value x and an
output value y. If we input x into the equation, the output is y.
We encounter many examples of this type of relationship every
day.



The cost to fill a tank with gasoline depends on how many gallons
are needed; the number of gallons is the input, and the cost is the
output
The distance traveled depends on the traveling time; input a time
and the output is a distance.
The growth of a plant depends on the amount of sun it gets; the
input is the amount of sun, and the output is growth.
10.2 Graphing Linear Equations in
Two Variables
1. Graph linear equations by plotting
ordered pairs.
2. Find intercepts.
3. Graph linear equations of the form
Ax + By = 0.
4. Graph linear equations of the form
y = k or x = k.
5. Use a linear equation to model data.
10.2.1: Graph linear equations by plotting
ordered pairs.
Infinitely many ordered pairs satisfy a linear equation in two
variables. We find these ordered-pair solutions by choosing as
many values of x (or y) as we wish and then completing each
ordered pair.
Some solutions of the equation x + 2y = 7 are graphed below.
Graph linear equations by plotting ordered
pairs. (cont’d)
Notice that the points plotted in the previous graph all appear
to lie on a straight line, as shown below.
Every point on the line represents a solution of the equation
x + 2y = 7, and every solution of the equation corresponds to a
point on the line.
 The line gives a “picture” of all the solutions of the equation
x + 2y = 7. Only a portion of the line is shown, but it extends
indefinitely in both directions, suggested by the arrowheads.
The line is called the graph of the
equation, and the process of plotting the
ordered pairs and drawing the line
through the corresponding points is
called graphing.

Graph linear equations by plotting ordered
pairs. (cont’d)
In summary, the graph of any linear equation in two variables
is a straight line.

Notice the word line appears in the name “lineear equation.”
Since two distinct points determine a line, we can graph a
straight line by finding any two different points on the line.
However, it is a good idea to plot a third point as a check.

Problem:
Graphing a Linear Equation
Graph 5 x  2 y  10.
Solution:
5  0  2 y  10
5x  2  0  10
2 y 1 0

2
2 0, 5


y  5
5 x 10

5
5
x  2
 2, 0
When graphing a linear equation, all three points should lie on the same
straight line. If they don’t, double-check the ordered pairs you found.
Problem:
2
Graph y  x  2.
3
Solution:
Graphing a Linear Equation
2
y   0  2
3
y  2
 0, 2
2
02  x22
3
2 3
3
 2  x 
3 2
2
2
4  2  x  2  2
3
2
3
 2  x
3
2
x  3
 3, 4
x 3
3,0
10.2.2: Find intercepts.
In the previous example, the graph
intersects (crosses) the y-axis at (0,−2)
and the x-axis at (3,0). For this reason
(0,−2) is called the y-intercept and (3,0)
is called the x-intercept of the graph.

The intercepts are particularly useful for graphing linear
equations. The intercepts are found by replacing, in turn, each
variable with 0 in the equation and solving for the value of the
other variable.

To find the x-intercept, let y = 0 and solve for x. Then (x,0) is
the x-intercept.

To find the y-intercept, let x = 0 and solve for y. Then (0, y)
is the y-intercept.

Problem: Finding Intercepts
Find the intercepts for 5x + 2y = 10. Then draw the
graph.
Solution:
5x  2  0  10
5 x 10

5
5
x2
x-intercept:
5  0  2 y  10
2 y 10

2
2
y 5
 2, 0 
y-intercept:
 0,5
When choosing x- or y-values to find ordered pairs to plot, be careful to
choose so that the resulting points are not too close together. This may
result in an inaccurate line.
10.2.3: Graph linear equations of the form
Ax + By = 0.
If A and B are nonzero real numbers, the graph of a linear
equation of the form
Ax  By  0
passes through the origin (0,0).
A second point for a linear equation that passes through the origin
can be found as follows:
1. Find a multiple of the coefficients of x and y.
2. Substitute this multiple for x.
3. Solve for y.
4. Use these results as a second ordered pair.
Graphing an Equation of the
Form Ax + By = 0
Problem:
Graph 4x − 2y = 0.
Solution:
12
1
4  6  2 y  0
24  2 y  24  0  24
2 y 2 4

2
2
y  12
4x  2  2  0
4x  4  4  0  4
4 x 4

4
4
x  1
10.2.4: Graphing linear equations of the
form y = k or x = k.
The equation y = −4 is the linear equation in which the
coefficient of x is 0. Also, x = 3 is a linear equation in which
the coefficient of y is 0. These equations lead to horizontal
and vertical straight lines, respectively.
 The graph of the linear equation y = k, where k is a real
number, is a horizontal line with y-intercept (0, k) and no
x-intercept.
The graph of the linear equation x = k, where k is a real
number, is a vertical line with x-intercept (k ,0) and no
y-intercept.

The equations of horizontal and vertical lines are often confused with
each other. Remember that the graph of y = k is parallel to the x-axis
and that of x = k is parallel to the y-axis.
Problem:
Graphing an Equation of the
Form y = k
Graph y = −5.
Solution:
The equation states that every value of y = −5.
Problem:
Graphing an Equation of the
Form x = k
Graph x − 2 = 0.
Solution:
After 2 is added to each side the equation states that
every value of x = 2.
10.2.5: Use a linear equation to
model data.
The different forms of linear equations from this section and the
methods of graphing them are given in the following summary.
Problem:
Use a Linear Equation to Model
Credit Card Debt
Use a) the graph and b) the equation to approximate
credit card debt in 1997, where x = 2.
Solution:
a) about 525 billion dollars
b)
y  38.7  2  450
y  77.4  450
1997
y  527.4
527.4 billion dollars.
10.3: The Slope of a Line
1. Find the slope of a line given two
points.
2. Find the slope from the equation of a
line.
3. Use slopes to determine whether two
lines are parallel, perpendicular, or
neither.
The Slope of a Line
An important characteristic of the lines we graphed in
Section 10.2 is their slant, or “steepness.”
One way to measure the steepness of a line is to compare the vertical change in the line with
the horizontal change while moving along the line from one fixed point to another. This measure
of steepness is called the slope of the line.

10.3.1: Find the slope of a line given two points.
To find the steepness, or slope, of the line in the figure
below, begin at point Q and move to point P. The vertical
change, or rise, is the change in the y-values, which is the
difference 6 − 1 = 5 units. The horizontal change, or run, is the
change in the x-values, which is the difference 5 − 2 = 3 units.
 The slope is the ratio of the vertical change in y to the
horizontal change in x.
vertical change in y  rise 
5
slope 

horizontal change in x  run  3
Count squares on the grid to find the change.
Upward and rightward movements are
positive. Downward and leftward movements
are negative.
Problem:
Find the slope of the line.
Solution:
6
m
1
m  6
Finding the
Slope of a Line
Find the slope of a line given two points. (cont’d)
The slope of a line is the same for any two points on the line.
The slope of a line can be found through two nonspecific
points. This notation is called subscript notation, read x1 as
“x-sub-one” and x2 as “x-sub-two”.

Moving along the line from the point (x1, y1) to the point
(x2, y2), we see that y changes by y2 − y1 units. This is the vertical
change (rise). Similarly, x changes by x2 − x1 units, which is the
horizontal change (run). The slope of the line is the ratio of
y2
− y1 to x2 − x1.



Traditionally, the letter m represents slope.
The slope of a line through the points (x1, y1) and (x2, y2) is
vertical change in y  rise 
y2  y1
m

horizontal change in x  run  x2  x1
if x1  x2 .
Finding Slopes
of Lines
Problem:
Find the slope of the line through (6, −8) and (−2,4).
Solution:
4   8
m
2  6
12

8
3

2
y2  y1
y1  y2
and
yield the same slope. Make sure to start with the
x2  x1
x1  x2
x- and y-values of the same point and subtract the x- and y-values of
the other point.
Find the slope of a line given two points. (cont’d)
Positive and Negative Slopes
A line with a positive slope rises (slants up) from left to right.
A line with a negative slope falls (slants down) from left to right.
Slopes of Horizontal and Vertical Lines
 Horizontal lines, with equations of the form y = k, have
slope 0.

Vertical lines, with equations of the
form x = k, have undefined slopes.

Finding the Slope
of a Horizontal Line
Problem:
Find the slope of the line through (2, 5) and (−1,5).
Solution:
55
m
1  2
0

3
0
Finding the Slope
of a Vertical Line
Problem:
Find the slope of the line through (3, 1) and (3,−4).
Solution:
4  1
m
33
undefined slope
5

0
10.3.2: Find the slope from the equation of
a line.
Consider the equation y = −3x + 5.
The slope of the line can be found by choosing two different
points for value x and then solving for the corresponding values
of y. We choose x = −2 and x = 4.
y  3 x  5
y  3 x  5
y  3 2  5
y  65
y  11
y  3 4  5
y  12  5
y  7
The ordered pairs are (−2,11) and (4, −7). Now we use the
slope formula.
11   7  18
m

 3
2  4
6
Find the slope from the equation of a line. (cont’d)
The slope, −3 is found, which is the same number as the
coefficient of x in the given equation y = −3x + 5. It can be
shown that this always happens , as long as the equation is
solved for y.

This fact is used to find the slope of a line from its equation,
by:


Step 1: Solve the equation for y.

Step 2: The slope is given by the coefficient of x.
Problem:
Finding Slopes
from Equations
Find the slope of the line 3x + 2y = 9.
Solution:
3x  2 y  3x  9  3x
2 y 3x  9

2
2
3
9
y  x
2
2
3
m
2
10.3.3: Use slopes to determine whether two
lines are parallel, perpendicular, or neither.
Two lines in a plane that never intersect are parallel. We use
slopes to tell whether two lines are parallel. Nonvertical parallel
lines always have equal slopes.
 Lines are perpendicular if they intersect at a 90° angle. The
product of the slopes of two perpendicular lines, neither of
which is vertical, is always −1. This
means that the slopes of perpendicular
lines are negative (or opposite)
reciprocals—if one slope1 is the nonzero
number a, the other is  a . The table to
the right shows several examples.
Deciding whether Two Lines
Are Parallel or Perpendicular
Problem:
Determine whether the pair of lines is parallel, perpendicular, or neither.
Solution:
x  3y  9
3x  y  4
3x  y  3x  4  3x
 y 4  3x

1
1
y  4  3x
1
  3   1
3
x  3y  x  9  x
3y 9 x
 
3 3 3
1
y  3 x
1
3 m
m3
3
The product of their slopes is −1, so they are perpendicular
10.4: Equations of a Line
1. Write an equation of a line by using its
slope and y-intercept.
2. Graph a line by using its slope and a
point on the line.
3. Write an equation of a line by using its
slope and any point on the line.
4. Write an equation of a line by using two
points on the line.
5. Find an equation of a line that fits a data
set.
10.4.1: Write an equation of a line
by using its slope and y-intercept.
Finding an Equation
of a Line
Problem:
Find an equation of the line with slope −1 and
Solution:
y-intercept (0,8).
y  x  8
10.4.2: Graph a line by using its slope
and a point on the line.

Step 1: Write the equation in slope-intercept form, if
necessary, by solving for y.
Step 2: Identify the y-intercept. Graph the point (0,b).

Step 3: Identify slope m of the line. Use the geometric
interpretation of slope (“rise over run”) to find another
point on the graph by counting from the y-intercept.

Step 4: Join the two points with a line to obtain the graph.
Problem:
Graphing a Line by Using the
Slope and y-intercept
Graph 3x – 4y = 8 by using the slope and y-intercept.
Solution:
3x  4 y  3x  8  3x
4 y
3x 8


4
4 4
3
y  x2
4
Slope intercept
form
Problem:
Graphing a Line by Using the
Slope and a Point
Graph the line through (2,−3) with slope
1
 .
3
Solution:
Make sure when you begin counting for a second point you begin
at the given point, not at the origin.
10.4.3: Write an equation of a line by using its
slope and any point on the line.
There is another form that can be used to write the equation of
a line. To develop this form, let m represent the slope of a line
and let (x1,y1) represent a given point on the line. Let (x, y)
represent any other point on the line.
y  y1
x  x1
y  y1
m  x  x1  
 x  x1 
x  x1
m  x  x1   y  y1
m

This result is the point-slope form of the equation of a line.
The point-slope form of the equation of a line with slope m
passing through point (x1,y1) is
Slope

y  y1  m  x  x1 
Given
point
Problem:
Using the Slope-Intercept
Form to Write an Equation
Write an equation, in slope-intercept form, of the line having slope −2 and passing through the
point (−1,4).
Solution:
y  mx  b
4  2  1  b
42  2b2
b2
The slope-intercept form is
y  2 x  2
Problem:
Using the Point-Slope Form to
Write Equations
Find the equation of the line through (5,2), with the slope
intercept form.
Solution:
1
 .Give the final answer in slope3
y  y1  m  x  x1 
1
y  2    x  5
3
1
5 6
y22   x 
3
3 3
1
11
y   x
3
3
Problem:
10.4.4: Finding the
Equation of a Line by Using
Two Points
Find an equation of the line through the points (2,5) and (−1,6). Give the final answer in slopeintercept form.
Solution:
y2  y1
m
x2  x1
65
m
1  2
1
m
3
y  y1  m  x  x1 
1
y  6    x   1 
3
1
1 18
y 66   x 
3
3 3
1
17
y  x
3
3
The same result would also be found by substituting the slope and
either given point in slope-intercept form and then solving for b.
Standard Form
Many of the linear equations in Section 10.1−10.3
were given in the form Ax + By = C, called standard
form, which we define as follows.
A linear equation is in standard form if it is written
Ax  By  C ,
as
where A, B, and C are integers, A > 0, and B ≠ 0.
A summary of the forms of linear equations follow
Problem:
10.4.5: Finding the
Equation of a Line That
Describes Data
Use
the points (1, 3362) and (7, 5491) to find an equation in
slope-intercept form that approximates the
data of the table. (Round the slope to the
nearest tenth.) How well does this equation
approximate the cost in year 5?
y2  y1
m
x2  x1
5491  3362
m
y  y1  m  x  x1 
7 1
y  3362  354.8  x  1 
2129
m
y  3362  3362  354.8 x  354.8  3362
6
y  354.8 x  3007.2
m  354.8
The equation gives y ≈ 4781 when x = 5, which is a
pretty good approximation.
Solution:
Competition
Problems
Find the value of y if the line that
contains (3, 4) and (4, 2) is
perpendicular to the line that
contains (6,y) and (22,3).
Answer:
-5
Write an equation in standard form
of the line that is perpendicular to
the line x + 2y = 10 and
has the same y intercept as the line
y – 1/2x = 3
Answer:
2x – y = -3
Write the equation of the line that
passes through the point (1, 2)
which has the same slope as the
line through (4, -1) and (3, 6).
Answer:
y = -7x + 9
Find the equation of the line that
passes through the points
(3,7) and (10,21).
Answer:
y = 2x + 1
Choose the equation of a line perpendicular
to the graph -9x + 3y -12 = 0.
(a) y = -⅓x + 4
(b) y = -3x + 4
(c) y = -x + 1
(d)y = 3x + 5
Answer:
(a) y = -⅓x + 4
The graph of the equation
2x + 6y = 1
does not cross which quadrant?
Answer:
III
Find the equation in standard form
of the line having slope of -1/4
and y-intercept of 10.
Answer:
x + 4y = 40
A line passes through the points
(3, –4) and (–2, 5).
What is the sum of its
slope and y-intercept?
Answer:
-2/5
Find the slope of the line passing
through (-5, 8) and (3, -2).
Answer:
-5/4
Write an equation of the line
containing the given point and
perpendicular to the given line.
(-6,2) & 3x -9y = 2
Answer:
y = -3x - 16
Give the equation of a line, in
standard form, that is
perpendicular to the graph of
¾x - ¼y = -½
and passes through the point
(2, -3).
Answer:
7x + 21y = -9