Download PPT

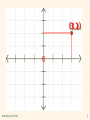
Graphs and Graphing Utilities(1.1)
Linear Equations (1.2)
Formulas and Applications(1.3)
Lect #4
H.Melikian/1100/04
Dr .Hayk Melikyan
Departmen of Mathematics and CS
[email protected]
1
Definitions: Rectangular coordinate system
The horizontal number line is the x-axis.
 The vertical number line is the y-axis.
 The point of intersection of these axes is their
zero points, called the origin.

5
4
Origin (0, 0)
3
2
1
-5 -4 -3 -2
-1
-1
-2
1
2
3 4
5
-3
-4
-5
H.Melikian/1100/04
2
Definitions
The axes divide the plane into four quarters,
called quadrants.
 Each point in the rectangular coordinate
system corresponds to an ordered pair of real
numbers, (x, y).

5
4
2nd quadrant
3
1st quadrant
2
1
-5 -4 -3 -2
-1
-1
-2
3rd quadrant -3
1
2
3 4
5
4th quadrant
-4
-5
H.Melikian/1100/04
3
Example
The first number in each pair, called the
x-coordinate, denotes the distance and direction from
the origin along the x-axis.
The second number in each pair, called the
y-coordinate, denotes the distance and direction
from the origin along the y-axis or along a line
parallel to the y-axis.
Plot the point (3,2).
Start at the origin and move 3 units to the right.
From that point, move 2 units up.
Now plot your point.
H.Melikian/1100/04
4
H.Melikian/1100/04
5
Graphs of equations




A relationship between two quantities can be expressed
as an equation in two variables, such as
y = 2 + x2
A solution of an equation in two variables, x and y, is
an ordered pair of real numbers with following property:
when the x-coordinate is substituted for x and ycoordinate is substituted for y in the equation, we obtain
a true statement.
The graph of an equation in two variables is the set of
all points whose coordinates satisfy the equation. One
method for graphing such equations is the point-plotting
method.
H.Melikian/1100/04
6
Text Example
Sketch the graph of y = x2 – 4.
Let x = 3, then y = x2 – 4 = 9 – 4 = 5.
The ordered pair (3, 5) is a solution to the
equation y = x2 – 4.
We also say that (3, 5) satisfies the equation.
H.Melikian/1100/04
7
Text Example Cont.
•
First, find several ordered pairs that are
solutions to the equation.
H.Melikian/1100/04
x
y = x2 – 4
-3
y = (-3)2 – 4 = 9 – 4 = 5
(-3, 5)
-2
y = (-2)2 – 4 = 4 – 4 = 0
(-2, 0)
-1
y = (-1)2 – 4 = 1 – 4 = -3
(-1, -3)
0
y = (0)2 – 4 = 0 – 4 = -4
(0, -4)
1
y = 12 – 4 = 1 – 4 = -3
(1, -3)
2
y = 22 – 4 = 4 – 4 = 0
(2, 0)
3
y = 32 – 4 = 9 – 4 = 5
(3, 5)
Ordered Pair (x, y)
8
Text Example Cont.
•
Now, we plot these ordered pairs as points in
the rectangular coordinate system.
5
4
3
2
1
-5 -4 -3 -2
-1
-1
-2
1
2
3 4
5
-3
-4
-5
H.Melikian/1100/04
9
Intercepts
An x-intercept of a graph is the x-coordinate of a
point where the graph intersects the x-axis.
 The y-coordinate corresponding to an x-intercept
is always zero.
 A y-intercept of an graph is the y-coordinate of a
point where the graph intersects the y-axis.
 The x-coordinate corresponding to an y-intercept
is always zero

H.Melikian/1100/04
10
Example
Graph 4y + 5x = 20.
Substitute zero for x:
4y = 20 or y = 5.
Hence, the y-intercept is (0,5).
Substitute zero for the y:
5x = 20 or x = 4.
Hence, the x-intercept is (4,0).
H.Melikian/1100/04
11
H.Melikian/1100/04
12
Linear Equations
Terms Involving Equations
3x - 1 = 2
Left Side
Right Side
An equation consists of two algebraic expressions joined by an equal sign.
3x – 1 = 2
3x = 3
x=1
H.Melikian/1100/04
1 is a solution or root of the equation
13
Definition of a Linear Equation
•
A linear equation in one variable x is an equation
that can be written in the form
•
ax + b = 0
•
where a and b are real numbers and a = 0.
H.Melikian/1100/04
14
Generating Equivalent Equations
An equation can be transformed into an equivalent equation by one or more of the following
operations.
Example
1. Simplify an expression by
removing grouping symbols and
combining like terms.
3(x - 6) = 6x - x
3x - 18 = 5x
2. Add (or subtract) the same
real number or variable
expression on both sides of the
equation.
3x - 18 = 5x
3x - 18 - 3x = 5x - 3x
-18 = 2x
3. Multiply (or divide) on both
sides of the equation by the same
nonzero quantity.
-18 = 2x
-9 = x
4. Interchange the two sides of
the equation.
-9 = x
x = -9
H.Melikian/1100/04
Subtract 3x from both
sides of the equation.
Divide both sides of the
equation by 2.
15
Solving a Linear Equation
•
•
•
•
Simplify the algebraic expression on each
side.
Collect all the variable terms on one side and
all the constant terms on the other side.
Isolate the variable and solve.
Check the proposed solution in the original
equation.
H.Melikian/1100/04
16
Text Example
Solve the equation: 2(x - 3) - 17 = 13 - 3(x + 2).
Solution
Step 1
Simplify the algebraic expression on each side.
2(x - 3) – 17 = 13 – 3(x + 2)
2x – 6 – 17 = 13 – 3x – 6
2x – 23 = - 3x + 7
H.Melikian/1100/04
This is the given equation.
Use the distributive property.
Combine like terms.
17
Text Example
Solve the equation: 2(x - 3) - 17 = 13 - 3(x + 2).
Solution
Step 2
Collect variable terms on one side and constant terms on
the other side. We will collect variable terms on the left by adding 3x to
both sides. We will collect the numbers on the right by adding 23 to both
sides.
2x – 23 + 3x = - 3x + 7 + 3x
5x – 23 = 7
5x – 23 + 23 = 7 + 23
5x = 30
H.Melikian/1100/04
Add 3x to both sides.
Simplify.
Add 23 to both sides.
Simplify.
18
Text Example
Solve the equation: 2(x - 3) - 17 = 13 - 3(x + 2).
Solution
Step 3
Isolate the variable and solve. We isolate the variable by
dividing both sides by 5.
5x = 30
5x/5 = 30/5
x=6
H.Melikian/1100/04
Divide both sides by 5
Simplify.
19
Text Example
Solve the equation: 2(x - 3) - 17 = 13 - 3(x + 2).
Solution
Step 4
Check the proposed solution in the original equation.
Substitute 6 for x in the original equation.
2(x - 3) - 17 = 13 - 3(x + 2)
?
2(6 - 3) - 17 = 13 - 3(6 + 2)
?
2(3) - 17 = 13 - 3(8)
?
6 – 17 = 13 – 24
-11 = -11
This is the original equation.
Substitute 6 for x.
Simplify inside parentheses.
Multiply.
This true statement indicates that 6 is the solution.
The solution set is {6}.
H.Melikian/1100/04
20
Types of Equations
•
•
•
Identity:An equation that is true for all real
numbers.
Conditional: An equation that is true for
at least one real number.
Inconsistent: An equation that is not true
for any real number.
H.Melikian/1100/04
21
Example
Determine whether the equation 3(x - 1) = 3x + 5 is an identity, a conditional
equation, or an inconsistent equation.
Solution
To find out, solve the equation.
3(x – 1) = 3x + 5
3x – 3 = 3x + 5
-3 = 5
This equation is inconsistent.
H.Melikian/1100/04
22
Text Example
Use the formula E = 0.177t + 71.35 to determine
the year of birth for which U.S. women can
expect to live 82 years.
First, substitute 82 for E in the formula:
82=0.177t + 71.35.
Next, solve for t by subtracting 71.35:
10.65=0.177t.
Now, divide both sides by 0.177.
60.17 = t
H.Melikian/1100/04
23
Solution cont.

The formula indicates that U.S. women born
approximately 60 years after 1950, or in 2010, can
expect to live 82 years.
H.Melikian/1100/04
24
Strategy for Problem Solving
Step 1: Read the problem carefully. Attempt to
state the problem in your own words and
state what the problem is looking for. Let x
(or any variable) represent one of the
quantities in the problem.
Step 2: If necessary, write expressions for any
other unknown quantities in the problem in
terms of x.
H.Melikian/1100/04
25
Strategy for Problem Solving
Step 3: Form a verbal model of the problems
conditions and then write an equation in x
that translates the verbal model.
Step 4: Solve the equation and answer the
question in the problem.
Step 5: Check the proposed solution in the
original wording of the problem, not in the
equation obtained from the words.
H.Melikian/1100/04
26
FORMULAS:
I = PRT
 Simple Interest=Principal *Rate * Time
 D = rt
 Distance = rate * time
 F = (9/5)C +32
degrees Fahrenheit = (9/5)degrees Celsius +32

H.Melikian/1100/04
27
Example
Two consecutive numbers have a sum of 91.
What are the numbers?
H.Melikian/1100/04
28
Solution
Step 1: Read the problem carefully. Attempt to
state the problem in your own words and
state what the problem is looking for. Let x
(or any variable) represent one of the
quantities in the problem.
Step 2: If necessary, write expressions for any
other unknown quantities in the problem in
terms of x.
Let x = The First Consecutive Number.
Let x + 1 = The Second Consecutive Number
H.Melikian/1100/04
29
Solution cont.
Step 3: Form a verbal model of the problems
conditions and then write an equation in x
that translates the verbal model.
x + (x + 1) = 91
H.Melikian/1100/04
30
Solution cont.
Step 4: Solve the equation and answer the question in
the problem.
x + (x + 1) = 91
subtract 1 from each side
divide each side by 2
---
2x + 1 = 91
-1 -1
2x = 90
--2
2
x
H.Melikian/1100/04
= 45
31
Solution cont.
Step 5: Check the proposed solution in the
original wording of the problem, not in the
equation obtained from the words.
H.Melikian/1100/04
32
Example

Solve the formula 4at+5y=2t+9y for t
H.Melikian/1100/04
33
Solution
4at + 5y = 2t + 9y
4at + 5y - 2t = 9y bring all t terms to one side
4at - 2t = 9y - 5y Move all other terms over
t(4a - 2) = 4y
Factor out t
t = 4y / (4a-2)
Divide by 4a-2
t = 2y/(2a - 1)
Cancel a factor of 2
H.Melikian/1100/04
34
Formulas and Applications
H.Melikian/1100/04
35