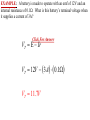Download electric current - college physics

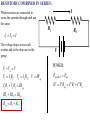
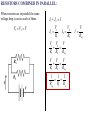
Direct Current
And Resistance
• Electric Current
• The Battery
• Resistance And Ohm’s Law
• Power
• Internal Resistance
• Resistors In Combination
• RC Circuits
Written by Dr. John K. Dayton
ELECTRIC CURRENT:
Electric current is the rate of flow of electric charge. By
convention, the direction of electric current is always the direction
of net flow of positive charge.
Current in conductors is the result of mobile electrons collectively
drifting in one direction. Ordinarily these mobile electrons move
at high speed in random directions. Collisions keep the velocity
distribution perfectly symmetric. If an electric field is applied, the
force on the electrons causes the velocity in one direction, that of
the force, to increase slightly. Electrons then drift slowly in that
direction. This drift velocity is like that of the wind in air and
produces the electric current. Note that when the current is the
result of moving negative charge, as with electrons, the direction
of the current is opposite that of the moving negative charge.
I
q
t
I is used to represent electric current. Since current is
the rate of flow of charge, it has SI units of C/s known
as the Amp, A.
EXAMPLE: A current of 3.0 A flows in a wire. How much
charge flows past a fixed point in 10 seconds?
q
I
 q  I t
t For Answer
Click
q   3.0 A 10s 
q  30C
NOTE:
The convention about current indicates this charge
is positive, flowing in a certain direction. However, in common
wire the actual movement of charge is in the opposite direction
and is negative (moving electrons).
THE VOLTAIC CELL AND BATTERIES:
A cell is an individual unit that produces a potential difference between
two metal terminals. It consists of two metal terminals with an
electrolytic material between them. As the terminals are oxidized by
chemical reaction with the electrolyte, the terminals become negatively
charged, one more than the other. Thus a potential difference occurs
between the terminals.
+
Symbol
for a cell
A battery is any collection of cells connected together.
When cells or batteries are connected in series the individual voltages add together.
When the cells are connected in parallel the output current is the sum of the currents
through each cell.
Electromotive force, emf, E, is any electric potential that can be used to sustain a
current.
The amp-hour rating of a battery is the product of current and time duration of that
current that can be sustained by the battery. A 3amp- hour rating will maintain 3 amps
for 1 hour or 1 amp for 3 hours, etc.. The amp-hour rating is a non-SI unit of charge,
the total amount of charge that flows through the battery.
EXAMPLE: A 12V battery is rated 3amp·hours. What is the total
charge and energy supplied by this battery?
Click For Answer
C
3600s
q  3 A  hr  3 1hr 
 10800C
s
hr
5
U  qV  10800C 12V  1.296 10 J
RESISTANCE AND OHM’S LAW:
The property of a substance called resistivity is a measure of the material’s ability to
inhibit the flow of current. Resistivity is usually designated by the symbol r.
Resistance to flow of current is designated by R and has SI units called Ohms, W.
If a substance is in the shape of a cylinder with length l and cross- section area A, then
its resistance R is proportional to l and inversely proportional to A.
l
R
A
The resistivity of the material out of which the cylinder is
made is the constant of proportionality. Resistivity has SI
units W∙m.
Rr
l
A
A
l
RESISTANCE AND OHM’S LAW:
For most substances resistivity increases with increasing temperature.
This increase is non-linear but may be approximated by a linear function.
r = the resistivity value at temperature
T to be calculated.
r  ro 1  T  To 
ro = the known resistivity value at
temperature To.
T = the temperature in oC or K at
which the resistivity will be calculated.
r
To = the temperature at which ro is
known.
r
To
T
 = the temperature coefficient of
resistivity.
EXAMPLE: A resistor is to be made from a 150m long aluminum wire
0.2mm in diameter. What is the resistor’s resistance at 20oC and at
2000oC?
For aluminum at 20 C r o  2.82 10 W  m,   3.9 10
o
at 20oC
at 2000oC
8
3
 C
o
Click For Answer 150m
l
R  r o   2.82 108 W  m 
 33.66W
2
A
  0.0002m 
r  r o 1   T  To  
1
3 o

r   2.82 10 W  m   1  3.9 10  C   2000 oC  20 oC  


r  2.46 107 W  m
l
150m
R  r   2.46 107 W  m 
 293.64W
2
A
  0.0002m 
8
1
RESISTANCE AND OHM’S LAW:
The symbol for a resistor in a circuit diagram is:
As current flows through a resistor it loses
energy. A rolling ball loses kinetic energy as
it rolls up a hill but its total energy is
constant. Current passing through a resistor
actually loses energy. The electric potential
on one side of a resistor is higher than on
other side. In a sense, the current has to
climb a potential hill to cross the resistor.
The difference in these potentials is called the
potential drop across the resistor and is
designated V. The current through the
resistor is I, and the resistance of the resistor
is R. SI units for these are volts, amps and
ohms. They are related by Ohm’s law.
V  IR
[Ohm’s Law]
V
V vs I
I
POWER SUPPLIED AND POWER LOSS:
The emf of a battery is defined
as the energy supplied by the
battery per unit charge.
U U t
E V 


q
t q
U
q
Psupplied 
I
t
t
1
V  Psupplied 
I
Psupplied  IV
Electric charge loses energy
as it flows through a resistor.
U  qV
U q

V
t
t
U
q
Ploss 
I
t
t
Ploss  I  IR  I 2 R
Ploss  I 2 R
V  IR
POWER SUPPLIED AND POWER LOSS:
In this circuit a battery and resistor (load) are
connected in series. Current from the battery
flows through wires to and through the resistor
and then back to the battery. When it leaves the
battery the current is at high energy. On its
journey through the circuit this energy is lost and
the current returns to the battery at low energy.
R
I
I
+
V
Neither current nor charge is consumed. Chemical energy within the battery is
converted to electric potential energy carried by the current leaving the battery. The
electric potential energy is lost as the current crosses the resistor where the energy is
converted to some other form, mostly thermal (known as joule heating.) As the current
moves through the battery, a chemical reaction pumps the current from low U to high U
and the journey is repeated. This will continue until the available chemical energy
within the battery is exhausted, being ultimately converted to thermal energy.
R
EXAMPLE: A 15W resistor is connected to a
45V power supply. What current flows through
the resistor? What power is supplied to the
circuit? What is the power loss by the resistor?
I
I
+
V
-
Click For Answer
V 45V
V  IR  I  
 3.0 A
R 15W
Psupplied  IV  3.0 A  45V  135.0W
Ploss  I R   3.0 A 15W  135.0W
2
2
INTERNAL RESISTANCE:
r
+
-
The voltage difference across the
terminals of a battery, VT, is the
result of the emf of the battery, E,
and its internal resistance, r.
E
VT  E  Ir
The Ir term is a voltage drop across the internal resistance of the battery. Thus, some
energy produced by the battery is lost internally as thermal energy. The voltage at the
terminals will be less than the emf of the battery.
EXAMPLE: A battery is made to operate with an emf of 12V and an
internal resistance of 0.1W. What is this battery’s terminal voltage when
it supplies a current of 3A?
Click For Answer
VT  E  Ir
VT  12V   3 A   0.1W 
VT  11.7V
RESISTORS COMBINED IN SERIES:
I
When resistors are connected in
series the currents through each are
the same.
I1  I 2  I
The voltage drops across each
resistor add to the drop across the
group.
V1  V2  V
R1
R2
V
POWER:
V1  I1R1 , V2  I 2 R2 , V  IReq
Psupplied  Plost
I1R1  I 2 R2  IReq
IV  I 2 Req  I 2 R1  I 2 R2
IR1  IR2  IReq
Req  R1  R2
RESISTORS COMBINED IN PARALLEL:
When resistors are in parallel the same
voltage drop is across each of them.
V1  V2  V
I1  I 2  I
V1
V2
V
I1  , I 2  , I 
R1
R2
Req
V1 V2
V


R1 R2 Req
V V
V


R1 R2 Req
1
1
1
 
Req R1 R2
RESISTORS COMBINED IN GENERAL:
Series:
Req   Ri
currents are equal.
Parallel:
1
1

Req
Ri
voltage drops are equal.
Psupplied  Plost
IV  I 2 Req   I i2 Ri
EXAMPLE: R1=10W and R2=15W
are connected in series to a 50V
battery. What are the currents
through, voltage drops across, and
power losses at each resistor?
Use Series equation:
P1  I R1   2 A 10W  40W
2
1
2
Req  R1  R2  10W Click
15W For Answer
2
2
P2  I 2 R2   2 A 15W  60W
Req  25W
Ptotal  P1  P2  100W
Vbat 50V
I eq 

 2A
2
2
Ptotal  I Req   2 A 25W  100W
R e q 25W
I1  I 2  I eq
in series
V1  I1 R1  2 A 10W  20V
V2  I 2 R2  2 A 15W  30V
EXAMPLE: R1=12W and R2=15W are
connected in parallel to a 18V battery. What
are the currents through, voltage drops and
power losses at each resistor?
Use parallel equation:
1
1 1
1
1
 


Req R1 R2 10W 15W
2
Click For Answer
2
P1  I1 R1  1.8 A  10W   32.4W
Req  6W
V
18V
I  bat 
 3.0 A
Req 6W
V1  V2  Vbat  18V in parallel
V1 18V
I1 

 1.8 A
R1 10W
V2 18V
I2 

 1.2 A
R2 15W
P2  I R2  1.2 A  1.5W   21.6W
2
2
2
Ptotal  P1  P2  54.0W
Ptotal  I Req   3 A   6W   54.0W
2
2
RC CIRCUITS:
An RC circuit consists of a battery,
switch, resistor and capacitor
connected in. series
C
R
V
When the switch is open no current flows.
When the switch is initially closed the initial current is given by Ohm’s
law: Io=V/R
As charge builds in the capacitor the voltage across the capacitor also
builds, but opposes the battery.
As the capacitor is charged to Q=CV the current decreases to zero.
CHARGING:
I (t )  I o e

Io
Time scale in units of t.
t
RC
t



RC
V (t )  Vo  1  e 


t
Qo
t



RC
Q (t )  Qo  1  e 


Vo
I o  , Vo  Vbattery , Qo  CVo
R
t
Vo
t
DISCHARGING:
I (t )  I o e

V (t )  Vo e
Io
Time scale in units of t.
t
RC
t

RC
Q (t )  Qo e

t
Qo
t
RC
t
Vo
I o  , Vo  Vbattery , Qo  CVo
R
Vo
t
RC TIME CONSTANT:
The product RC has units of time and is referred to as the RC time
constant usually designated by the symbol t.
t is the time it takes the current to (or from) a capacitor to decrease from
Io to Io/e.
Io
t  RC
Io
 .37 I o
e
.37Io
t
t
EXAMPLE: A resistor of 750,000W is
connected to a 3.7mF capacitor and 24V battery
in series with an open switch. The capacitor is
completely uncharged. How long will it take
the capacitor to reach 80% of its maximum
charge after the switch is closed?
C
R
V
  ln e 
  ClicklnFor.2Answer
t
.8Q  Q 1  e 
ln .2   
RC
Q(t )  Qo 1  e
t
 RC
t
 RC
t
 RC
o
o
.8  1  e
t
 RC
.2  e
t
 RC
.2  e
t
 RC
t   RC ln .2 
t    750,000W    3.7  106 F   ln .2 
t  4.47 s
End Of Presentation