Download PV Diagrams

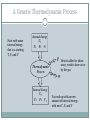
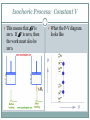
PV Diagrams
THERMODYNAMICS
A Generic Thermodynamic Process
Start with some
internal energy
due to a starting
T, P, and V
Internal Energy
T1
U1
P 1 V1
Q Heat is added or taken
away, work is done on or
by the gas
Thermodynamic
Process
W
Internal Energy
T2
U2
P 2 V2
You end up with an new
amount of internal energy,
with new T, P, and V
Many engines that do work involve pistons and
cylinders.
 A cylinder is tube and a piston is a solid cylindrical
device that exactly fits into the cylinder so that there
is very little gap between the piston and the side of
the cylinder.
piston
cylinder
Pistons and Cylinders
 The piston can move up and down in the cylinder.
 Inside the cylinder, under the piston, is a gas.
 The gas cannot escape around the piston.
 Push down on the piston and the gas is compressed into
a smaller volume.
 Pull up on the piston and the gas expands into a larger
volume.
 The motion of the piston involves work. If you do work
on the piston, you make it move. If the gas expands or is
compressed causing the piston to move, then work is
done on the piston (the gas is doing the work).
isobaric process: constant P
 If you add heat to the cylinder,
the gas expands and pushes the
piston upwards, doing work on it.
We make a major assumption –
that the pressure stays constant.
This is actually reasonable. The
area on the top of the piston
doesn’t change, so the force
exerted on it by the atmosphere
is constant. When the piston
rises to some position, the force
pushing down is still the same, so
the force inside pushing up must
be the same as well. Since this
force comes from the pressure,
the pressure must still be the
same.
y
Gas expands at constant pressure
moving piston a distance of  y
isobaric process: constant P
 What a P-V Diagram
would look like
How to Find the Amount of Work Done

The piston has moved a distance of  y.

A force pushed the piston upward.

Work happens when a force causes an object to move.

So can we figure out how much work was done on the piston?

Well, we know that pressure is the force divided by the area it acts on: P=F/a

The force exerted by the pressure is equal to:
F = PA















The definition of work is: W=Fd
So, plugging in the value of the force, we get:
W  Fd
  PA d
 PAd
We know that the area of this cylinder multiplied by its height is its change in volume:
Therefore, plugging this in for Ad we get:
So
W  PV
W  PAd
 P  V   PV
V  Ad
Sign of work
How to Find the Amount of Work Done
 The area under the curve
is equal to the work that
is done.
 This is also true for any
graph of pressure vs
volume. The area under
the curve is always equal
to the work.
W  PV
Work Done Using a P-V Diagram
 note that in a cyclic
process the gas is taken
through a cycle of
operations and brought
back to the original state.
If the cycle is clockwise
as in the present case,
work is done by the gas.
So the work is negative.
Further, the area
enclosed by the closed
curve gives the work
done during one cycle.
Isochoric Process: Constant V
 This means that V is
zero. If V is zero, then
the work must also be
zero.
 What the P-V diagram
looks like
Isothermal Process: Constant T
 During this process heat
can enter and leave the
gas but the total energy
in the gas will not
change. ∆U=ZERO
U  Q  W
0  Q W
Q  W
 What the P-V diagram
looks like
Adiabatic Processes:
Q  0
 In an adiabatic process, heat is neither added or
taken away from the system.
 This means that the first law can be simplified:
U  Q  W

U  W
 What this means is that work is done by the system
at the expense of internal energy.
Adiabatic Processes
 Adiabatic processes are very common. There are two simple ways to have
one take place:
1. The system can be insulated so that heat can neither enter nor leave.
Joule’s “heat equivalent” experiment was adiabatic. The tub of water was
insulated so the water would not absorb heat from its surroundings.
Instead the work done on the water by the paddles increased the internal
energy of the system - the temperature went up.
2. The other way to have an adiabatic process (this is actually called a “near
adiabatic process”) is to have it happen very quickly. The process happens
so fast that there is no time for heat to be transferred.
 The combustion of gasoline in an engine is considered to be adiabatic
because each combustion step happens in a very short time – a few
hundredths (or less) of a second.
Adiabatic Processes
 In an adiabatic process the following can happen:
1. a gas that is adiabatically expanded will lose
internal energy (U ) and become cooler.
2. a gas that is adiabatically compressed will gain U
and become warmer.
Compress air from your lungs by
puckering your lips. When it leaves
your mouth, it expands adiabatically,
thus it cools
Sample Problems
 One mole of monatomic ideal
gas is enclosed under a
frictionless piston. A series of
processes occur, and
eventually the state of the gas
returns to its initial state with
a P-V diagram as shown
below. Answer the following
in terms of P0, V0, and R.
1. Find the temperature at each
vertex.
2. Find the change in internal
energy for each process.
3. Find the work by the gas done
for each process.
1. Find the temperature at
each vertex.
 Use the gas law to find the
temperatures at A, B, C
2. Find the change in
internal energy for each
process.

Since the internal energy depends only on
temperature, the change in internal energy
for each process depends only on the
temperature difference that occurs during the
process:
3. Find the work by the gas
done for each process.

To find the work done by the gas, find
the area under each segment,
remembering the sign convention.