* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Introduction to Probability: Counting Methods
Survey
Document related concepts
Transcript
Introduction to Probability:
Counting Methods
Rutgers University
Discrete Mathematics for ECE
14:332:202
Why Probability?
We can describe processes for which the
outcome is uncertain
By their average behavior
By the likelihood of particular outcomes
Allows us to build models for many physical
behaviors
Speech, images, traffic …
Applications
Communications
Speech and Image Processing
Machine Learning
Decision Making
Network Systems
Artificial Intelligence
Used in many undergraduate courses (every
grad course)
Methods of Counting
One way of interpreting probability is by the
ratio of favorable to total outcomes
Means we need to be able to count both the
desired and the total outcomes
For illustration, we explore only the most
important applications:
Coin flipping
Dice rolling
Card Games
Combinatorics
Mathematical tools to help us count:
How many ways can 12 distinct objects be
arranged?
How many different sets of 4 objects be chosen
from a group of 20 objects?
-- Extend this to find probabilities …
Combinatorics
Number of ways to arrange n distinct objects
n!
Number of ways to obtain an ordered sequence
of k objects from a set of n:
n!/(n-k)! -- k permutation
Number of ways to choose k objects out of n
distinguishable objects:
n
n!
k k!(n k )!
This one comes up a lot!
Set Theory and Probability
We use the same ideas from set theory in our
study of probability
Experiment
Outcome – any possible observation of an exp.
Roll a six
Sample Space – the set of all possible outcomes
Roll a dice
1,2,…6
Event – set of outcomes
Dice rolled is odd
Venn Diagrams
Outcomes are mutually exclusive – disjoint
S
2
1
4
3
5
6
Event A
Outcomes
An Example from Card Games
What is the probability of drawing two of the same
card in a row in a shuffled deck of cards?
Experiment
Event Space
Pulling two cards from the deck
All outcomes that describe our event:
Two cards are the same
Sample Space
All Possible Outcomes
All combinations of 2 cards from a deck of 52
Sample Space/Event Space
Venn Diagram
Event Space (set of favorable outcomes)
S
all possible
outcomes
{A,A}
{K,2}
Calculating the Probability
# outcomes _ in _ event _ space
P(Event) =
# outcomes _ in _ sample _ space
Expressed as the ratio of favorable outcomes to
total outcomes
-- Only when all outcomes are EQUALLY LIKELY
Probabilities from Combinations
Rule of Product:
52
52!
1326
2
2
!
(
52
2
)!
Total number of two card combinations?
We need to find all the combinations of suit and value that
describe our event set: use rule of product to find the number
of combinations
First, we find number of values – 13 choices, and choices of
suits: 4
4!
6
2 2!(4 2)!
to give our number of possible outcomes 13*6 = 78
Probability(Event) = 78/1326 = 0.0588
Probabilities from Subexperiments
Only holds for independent experiments
Let’s look at the last problem:
Two subexperiments:
First can be anything 52/52 = 1
Second, must be one of the 3 remaining cards of the
same value from 51 remaining cards 3/51 = 0.588
An Example from Dice Rolling
Experiment: Roll Two (6-sided) Dice
Event: Numbers add to 7
Sample Space: (all possible outcomes)
S = 1,1 1, 2 1,3 1, 4 1,5 1, 6
2,1
3,1
4,1
5,1
6,1
2, 2
3, 2
4, 2
5, 2
6, 2
2,3
3,3
4,3
5,3
6,3
2, 4
3, 4
4, 4
5, 4
6, 4
2,5
3,5
4,5
5,5
6,5
2, 6
3, 6
4, 6
5, 6
6, 6
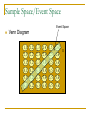
Sample Space/Event Space
Event Space
Venn Diagram
1,1
2,1
3,1
4,1
5,1
6,1
1, 2
2, 2
3, 2
4, 2
5, 2
6, 2
1,3
2,3
3,3
4,3
5,3
6,3
1, 4
2, 4
3, 4
4, 4
5, 4
6, 4
1,5
2,5
3,5
4,5
5,5
6,5
1, 6
2, 6
3, 6
4, 6
5, 6
6, 6
S
Calculating Probability
P(Event) = # outcomes _ in _ event _ space
# outcomes _ in _ sample _ space
= 6/36 = 1/6
Side Note
Probability is something we calculate “theoretically” as a value
between 0 and 1, it is not something calculated through
experimentation (that is more statistics).
Just because you roll a dice 100 times, and it came up as a 1
20 times, does not make P(roll a 1) = 0.2
It would be the limiting case in doing an infinite number of
experiments, but this is impossible.
So, call your calculated values the “probability”, and your
experimental values the “relative frequency”.