Download Graphing the Set of All Solutions

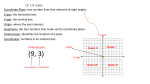
Introduction
In an equation with one variable, x, the solution will be
the value that makes the equation true. For example:
1 is the solution for the equation x = 1.
2 is the solution for the equation 2x = 4.
The solution of an equation with two variables x and y is
the pair of values (x, y) that make the equation true. For
example:
(1, 2) is a solution to the equation y = 2x because the
statement 2 = 2 is true.
(1, 3) is not a solution for y = 2x because the
statement 3 = 2 is false.
1
3.1.1: Graphing the Set of All Solutions
Introduction, continued
The pairs of values (x, y) are called ordered pairs, and
the set of all ordered pairs that satisfy the equation is
called the solution set. Each ordered pair in the
solution set represents a point in the coordinate plane.
When we plot these points, they will begin to form a
curve. A curve is a graphical representation of the
solution set for the equation. In the special case of a
linear equation, the curve will be a straight line. A linear
equation is an equation that can be written in the form
ax + by = c, where a, b, and c are rational numbers. It
can also be written as y = mx + b, in which m is the
slope, and b is the y-intercept.
2
3.1.1: Graphing the Set of All Solutions
Introduction, continued
It is important to understand that the solution set for
most equations is infinite; therefore, it is impossible to
plot every point. There are several reasons the solution
set is infinite; one reason is that there is always a
number between any two numbers x1 and x2, and for
that number there will be a y that satisfies the equation.
So when we graph the solution set for an equation, we
plot several points and then connect them with the
appropriate curve. The curve that connects the points
represents the infinite solution set to the equation.
3
3.1.1: Graphing the Set of All Solutions
Key Concepts
• A solution to an equation with two variables is an
ordered pair, written (x, y).
• Ordered pairs can be plotted in the coordinate plane.
• The path the plotted ordered pairs describe is called
a curve.
• A curve may be without curvature, and therefore is a
line.
4
3.1.1: Graphing the Set of All Solutions
Key Concepts, continued
• An equation whose graph is a line is a linear equation.
• The solution set of an equation is infinite.
• When we graph the solution set of an equation, we
connect the plotted ordered pairs with a curve that
represents the complete solution set.
5
3.1.1: Graphing the Set of All Solutions
Common Errors/Misconceptions
• believing the number of solutions an equation has is
limited to points seen on the graph
• incorrectly evaluating the equation for different given
values
• incorrectly plotting ordered pair solutions on a
coordinate plane
6
3.1.1: Graphing the Set of All Solutions
Guided Practice
Example 2
Graph the solution set for the equation y = 3x.
7
3.1.1: Graphing the Set of All Solutions
Guided Practice: Example 2, continued
1. Make a table.
Choose at least 3 values
for x and find the corresponding
values of y using the equation.
x
–2
–1
y
1
9
1
3
0
1
1
3
2
9
8
3.1.1: Graphing the Set of All Solutions
Guided Practice: Example 2, continued
2. Plot the ordered
pairs in the
coordinate
plane.
9
3.1.1: Graphing the Set of All Solutions
Guided Practice: Example 2, continued
3. Notice the points do not fall on a line.
The solution set for y = 3x is an exponential curve.
Connect the points by drawing a curve through them.
Use arrows at each end of the line to demonstrate
that the curve continues indefinitely in each direction.
This represents all of the solutions for the equation.
10
3.1.1: Graphing the Set of All Solutions
Guided Practice: Example 2, continued
✔
11
3.1.1: Graphing the Set of All Solutions
Guided Practice: Example 2, continued
12
3.1.1: Graphing the Set of All Solutions
Guided Practice
Example 3
The Russell family is driving 1,000 miles to the beach
for vacation. They are driving at an average rate of 60
miles per hour. Write an equation that represents the
distance remaining in miles and the time in hours they
have been driving, until they reach the beach. They plan
on stopping 4 times during the trip. Draw a graph that
represents all of the possible distances and times they
could stop on their drive.
13
3.1.1: Graphing the Set of All Solutions
Guided Practice: Example 3, continued
1. Write an equation to represent the
distance from the beach.
Let d = 1000 – 60t, where d is the distance remaining
in miles and t is the time in hours.
14
3.1.1: Graphing the Set of All Solutions
Guided Practice: Example 3, continued
2. Make a table. Choose values for t and find
the corresponding values of d.
The trip begins at time 0. Let 0 = the first value of t.
The problem states that the Russells plan to stop 4
times on their trip. Choose 4 additional values for t.
Let’s use 2, 5, 10, and 15.
Use the equation d = 1000 – 60t to find d for each
value of t. Fill in the table.
15
3.1.1: Graphing the Set of All Solutions
Guided Practice: Example 3, continued
t
d
0
1000
2
880
5
700
10
400
15
100
16
3.1.1: Graphing the Set of All Solutions
Distance remaining in miles
Guided Practice: Example 3, continued
3. Plot the ordered
pairs on a
coordinate plane.
Time in hours
17
3.1.1: Graphing the Set of All Solutions
Guided Practice: Example 3, continued
4. Connect the points by drawing a line.
Do not use arrows at each end of the line because
the line does not continue in each direction. This
represents all of the possible stopping points in
distance and time.
18
3.1.1: Graphing the Set of All Solutions
Distance remaining in miles
Guided Practice: Example 3, continued
Time in hours
✔
19
3.1.1: Graphing the Set of All Solutions
Guided Practice: Example 3, continued
20
3.1.1: Graphing the Set of All Solutions