* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download TOPIC 3. Electric Currents ELECTRIC CURRENTS
Galvanometer wikipedia , lookup
Opto-isolator wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Electric charge wikipedia , lookup
Electric battery wikipedia , lookup
Rectiverter wikipedia , lookup
Battery charger wikipedia , lookup
Current mirror wikipedia , lookup
Nanogenerator wikipedia , lookup
Electrical ballast wikipedia , lookup
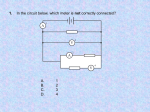
TOPIC 3. Electric Currents ELECTRIC CURRENTS What causes charges to flow, and what hinders the free flow of charge? The most important practical applications of electrical phenomena are in the innumerable forms of electronic devices. In these, it is the motion of electrical charges that takes center stage. All materials contain huge numbers of both positive and negative electrical charges (in the form of protons and electrons comprising every atom of matter), and in most cases these charges are pretty much fixed in position they don't move around a lot. However in certain materials for instance in metals charged particles can move. (In metals it is the negative charges - the electrons that actually move. We will however pretend that the moving charges are positive in order to simplify the discussion.) As noted earlier, these materials are called "conductors." In order to get the charges to start moving a force must act on them, and so an electric field must be present. You can imagine, as an example, a cylindrical piece of metal inside of which there is a uniform electric field, pointing along the length of the cylinder. If you stand at one fixed position in the cylinder and count the charges as they go past that point, you can measure the rate of flow of charge as a function of time. The term that is used to describe this rate of flow of charge is "current," and the symbol for current is M . (The unit of current is the "ampere," symbol "A.") If an amount of charge equal to ?; flows past a particular point in a time ?>, the current M is defined by this equation: ; Mœ ? 1 ampere œ 1 coulomb/second ?> We will always assume that the flow of current is "steady," that is, that the flow of charge continues without a stop and that the rate of flow does not change. Ask yourself: In that case, will the number of charges that flow past line B every second be larger than, smaller than, or the same as the number that flow past line A every second? The answer is: the same. If fewer charges flow past line B than flow past line A, that would mean that some charges are getting "trapped" between lines A and B. If that continued long enough, something disastrous would happen maybe the wire would explode! All those charges piling up in the same place would create a huge repulsive force that could not be contained. So this could not be a characteristic of "steady" flow of current. On the other hand, if more charges flowed past line B than flow past line A, that would mean that some extra charges must be sneaking in to the wire somewhere between A and B. There would have to be some external source of charge besides the charges already present in the wire. This also is not a characteristic of "steady" flow of charge, and so it too can not happen. We say, then, that current is "conserved," which means that the amount of charge flowing past any one point in the material is the same as that flowing past any other point, in a given amount of time. This will still hold true even if we place some obstacle in the path of the moving charges (for instance, some piece of material which offers more resistance to the flow of the charges). As long as the flow is steady, the current will be the same everywhere throughout any unbroken chain of conducting materials in direct contact with each other. Now, we have just implied that some materials offer more "resistance" to the flow of charge than do other materials. (Materials that hinder the flow of charge are called "resistors." The symbol for resistance is "V ," and it is measured in units called "ohms" [symbol: H].) The reason is that in some materials, the charges as they move have a large number of collisions with the atoms in the material. In the course of these collisions, the charges lose some energy (which is transferred to the atoms of the material). Because of this continual loss of energy, the moving charges require a force provided by an electric field if they are to continue to flow. Experiments show that the kinetic energy of the flowing charges remains nearly constant; however, their total energy decreases as they flow through a resistor. So the work done by nonconservative forces is negative. Question: As charges flow through a resistor, does their potential energy increase, decrease, or remain the same? Answer: PE decreases. The energy lost by the flowing charges is transferred to the material of the resistor. As a result, the resistor will heat up, and may even give off light. At some point, the energy of the moving charges will have to be replenished if the flow of charge is to be "steady." (We will see later on that this energy restoration process takes place when the charges flow through a battery.) What actually happens in the resistor is this: the electric force on the charges causes them to speed up briefly; however, before traveling more than a very tiny distance less than 109 m they collide with an atom and are slowed back down. During the collision, they transfer the energy they gained while speeding up to the atoms of the resistor. Then, this process is repeated trillions of times per second. The net result is that the average kinetic energy of the moving charges remains essentially constant. Their potential energy, and so their total energy, decreases, and there is a net transfer of energy from the moving charges, to the material of the resistor. Now, let's think about how the amount of current flow through a resistor will be affected by the amount of resistance (a large resistance would correspond to a large value of "V "). Question: All other things being equal, will increasing the value of V result in the amount of current flow increasing, decreasing, or remaining the same? Answer: Decreasing. Actually, this is really a definition of resistance: more resistance means a bigger obstacle to current flow, so less current will flow (all other things being equal). What about the relation between the amount of current flow, and the amount of T I lost by the charges as they flow through the resistor? Instead of discussing the potential energy, it is more convenient to refer to the change in electrical potential (i.e., T I per unit charge). Let us first decide whether the charges flow from high Z to low Z , or the other way around. Question: As positive charges flow through a resistor, does their potential Z increase, decrease, or remain the same? Answer: Decrease. Since their T I decreases and Z œ T IÎ; , a smaller T I implies a smaller Z (since ; 0). Next, let's consider the absolute value of the change in potential, l?Z l. We now have come to an extremely important point. Question: Suppose we have two identical resistors both with the same resistance V and one of the resistors has a larger potential difference l?Z l between its two ends. Will the amount of current flow through the resistor with the larger l?Z l be larger, smaller, or the same as the amount of current flow through the resistor with the smaller l?Z l? Hint: Consider the relative magnitude of the electrical force acting on the charges in each resistor. Answer: Larger. As discussed in the notes on electric potential, a larger l?Z l implies a larger electric field magnitude I (as long as the resistors are otherwise identical). A larger I means a larger magnitude of electrical force (since J œ ;I ). This stronger force provides more "push" to the charges, and gives them a chance to speed up a bit more before they are slowed down again by a collision. Therefore, more charges per second are able to flow past a given point, and so the current M is larger. [Even though the charges are going slightly faster, the change in their average kinetic energy is still extremely small.] We can put together our conclusions about the effect of resistance and potential difference on current flow in the form of a simple mathematical formula. Question: Which of these equations is consistent with the behavior of current flow we have just discussed: (A) M œ V ?Z ; (B) M œ VÎ?Z ; (C) M œ ?Z ÎV ; (D) M œ 1Î(V ?Z ); (E) M œ constant [independent of V and ?Z ]. Answer: (C) M œ ?Z ÎV . This relationship is consistent with our expectations, since M increases when ?Z increases, but M decreases when V is larger. However, the exact proportionality between M and ?Z represented in this equation does not always hold for every material. It is true often enough, though, to be called "Ohm's law." It is often a very good approximation, and we will always assume that it is true for the systems that we examine. However, it is NOT a fundamental law of physics it's just a relationship that holds for many systems. Let's look at an arrangement of two different resistors V1 and V2 connected by "perfectly conducting" wires. The arrow shows the direction of flow of current. Question: Will the T I of the flowing charges at point B be larger, smaller, or the same as the T I of those same charges at point A? Answer: Smaller. The charges lose T I as they flow through a resistor. Question: Will the value of Z at point B be larger, smaller, or the same as its value at point A? Answer: Smaller. Since the T I of the positive charges is less at point B than at point A, the potential Z must also be smaller at B. Now, lets use "Ð?T IÑAB " to symbolize the change in T I as the charges move from point A to point B, and "Ð?T IÑBC " for the change as they move from B to C, etc. Question: Will Ð?T IÑAC be larger, smaller, or equal to the quantity [Ð?T IÑAB Ð?T IÑBC ]? Answer: Equal to. The total amount of potential energy lost by the charges during the full trip from A to C equals the sum of potential energy losses accumulated first from A to B, and then from B to C. QUESTIONS Prerequisite Concepts: • Definitions of current, "voltage" [potential difference], resistance • Positive charges flow through resistors in direction of decreasing potential • Ohm's law: M œ ?Z ÎV • Current is conserved as it flows through conductors and resistors • Assumption: conducting wires are "ideal" (Vwire œ ?Zwire œ 0) Question 1. The same current M0 enters each of three resistors as shown below. The resistors have unequal magnitudes, and V3 V2 V1 . What will be the relationship among the magnitudes of the current leaving the three resistors? M0 R1 M1 (1) M1 M2 M3 M0 R2 (2) M1 M2 M3 M2 R3 M0 M3 (3) M1 œ M2 œ M3 Question 2. Current is flowing through a set of two identical resistors connected by wires as shown below. The magnitude of the current at three different points is indicated by M1 , M2 , and M3 . Which of these could be the relationship among M1 , M2 , and M3 ? M1 M2 M3 (1) M2 œ "# M1 and M3 œ "# M2 (2) M2 œ "# M1 and M3 œ "# M2 (3) ÐM1 M2 Ñ œ ÐM2 M3 Ñ Á 0 (4) M1 œ M2 œ M3 (5) M2 œ "# M1 and M3 œ M1 Question 3. The current flows through the resistor in the direction shown. Which of the following statements is true? (1) The potential at A is the same as at B. M (2) The potential at A is higher than that at B. (3) The potential at A is smaller than that at B. A B (4) There is not enough information to compare the potentials at A and B. p Question 4. In the figure below, five different resistors are shown, each with a conducting wire leading into it and another leading out of it. The electric potential at both ends of each resistor is shown. Determine the current through each resistor and find (1) which resistor has the greatest current through it, and (2) which resistor has the smallest current through it. (1) 5H (2) 4H (3) 3H 5V 3V (4) 6V 4H 8V 4V (5) 4V 17 V 18 V 2H 3V 6V Question 5. In this figure, current M1 flows through the left resistor and current M2 flows through the right resistor. Both resistors have the same value V . What is the ratio of M1 to M2 ? M1 p 3V M1 ÎM2 œ (1) 1 (2) 2 M2 V (3) 3 p 2V 6V (4) 1/2 (5) 1/3 V (6) 2/3 3V Mp Question 6. If the potential at point A doubles (i.e., ZA p 2 ZA ), what happens to the potential at point B? A V (1) ZB p 4ZB (2) ZB p 2ZB (3) ZB p 0.5 ZB (4) ZB p ZA ZB (5) ZB doesn't change (6) can't determine B Question 7. Using the notation ?ZAB ´ ZA ZB , which of the follow relationships must hold for the potential difference between points A and D? Mp A B V1 C V2 (1) ?ZAD ?ZAB ?ZBC ?ZCD (3) ?ZAD ?ZAB ?ZBC ?ZCD V3 D (2) ?ZAD œ ?ZAB ?ZBC ?ZCD (4) not enough information to answer Question 8. In the figure below, six different resistors are shown, each with a conducting wire leading into it and another leading out of it. The electric potential at both ends of each resistor is shown. Draw an arrow below each resistor, indicating the direction of the current through that resistor. Rank the magnitudes of the current flows, from largest to smallest, using the or œ to compare adjacent currents. For example, MA MB œ MC MD ME œ MF would mean MA is the largest current, followed by MB and MC which are equal, etc. (A) 1H 5V (D) 4V (B) 3V 2H 4V (E) 9V 2H 14 V (C) 1V 4H 18 V (F) 11 V 6V 2H 19 V 8H 13 V Ranking: (largest) _____________________________________________ (smallest) Also, for each case, determine the direction in which the current is flowing. Question 9. In this figure, current is flowing through a set of five resistors connected to each other by conducting wires. The electric potential is indicated at several points marked by dots. Rank the magnitudes of the resistances starting with the largest magnitude, using and œ signs as in Question 8. (A) V1 (B) V2 (C) V3 (D) V4 (E) V5 18 V 15 V 10 V 9V 7V 5V Ranking: (largest) _____________________________________________ (smallest) Question 10. A 5.0-A current is flowing through the set of resistors shown. The point E where the electric potential is 0 volts is indicated. Determine the electric potential at the following points: (A) __________ (B) __________ (C) __________ (D) __________ (E) 0 V Also, what is ?ZAE , the magnitude of the potential difference between points A and E? ?ZAE œ _________________ ----------------------------------------------------------------Question 11. If this set of resistors were replaced by a single resistor, and the same 5.0-A current were to flow, what would the value V of that resistor have to be in order to maintain the same potential difference between points A and E? V œ _________________ Note: This is called the "equivalent resistance" Veq of that set of resistors. What is the sum of the magnitudes of the individual resistors in this set? ______________ Compare the sum with the equivalent resistance; is the sum larger, smaller, or the same? Question 12. A 3.0-A current is flowing through the set of resistors shown. The point C where the electric potential is 9 volts is indicated. Determine the electric potential at the following points: (A) __________ (B) __________ (C) 9 volts (D) __________ (E) __________ What is the potential difference between points A and E? ?ZAE œ _________________ Question 13. If this set of resistors were replaced by a single resistor, and the same 3.0-A current were to flow, what would the value V of that resistor have to be in order to maintain the same potential difference between points A and E? V œ _________________ Compare this with the sum of the individual resistances. Question 14. In the figure below, a current of 3.0-A is flowing in the direction shown, and the point at which the electric potential equals 32 V is indicated. On the figure, write the value of the potential at all points indicated by large dots. Also, find the equivalent resistance of the set of resistors. Veq œ _________________ Question 15. In the figure below, an unknown current is flowing. Find the direction and magnitude of the current, and then write the value of the electric potential on the figure at all points indicated by large dots. Also find the equivalent resistance of the set of resistors. M œ _______________ Veq œ _______________ Question 16. In the figure below, a current of 5 A is flowing in the direction shown. On the figure, write down the value of all the resistors and find the equivalent resistance of the set of resistors. Veq œ _______________ Series Electric Circuits What happens when current flows in a circuit? Up until now, we have examined the flow of electric current through wires and resistors in somewhat artificial situations. That is, they're "artificial" because the charges have been flowing in one end of the resistors and then out the other end, without our knowing where the charges came from, and also without knowing to where they're going. We have said that the charges lose energy as they flow through the resistors, but we have not said what is providing energy to the charges. (If nothing was providing energy to them, the charges in the current would soon lose all their energy and could no longer flow through the resistors.) We have concluded that there must be an electric field present (and so a ?Z ) to provide a force that "pushes" the charges through the resistor. However, we haven't said what provides the source charges to create that electric field. We have assumed that the flow of current is "steady" and continuous - without a pile-up of charge in any one location. One arrangement that could achieve this is to have the charges flow continuously in a closed path (for instance, in a circular route). Such a continuous closed path for the flow of current is called an electric circuit. A device that is very often used to provide energy to charges flowing in a current is the battery (see the notes on electric potential). The battery also provides the source charges that create the electric field in the wires. So we can now illustrate a very simple circuit, including a resistor connected to a battery with "perfectly conducting" wires, with a diagram such as this: (We have indicated four different points in this circuit A, B, C and D for the discussion to follow, and we have also showed the direction of flow of current I.) In order to discuss this circuit, we must recall our definition of "perfectly conducting" wires. We assume that all wires (indicated in the circuit diagram by straight line segments) are "perfect conductors" which do not hinder the flow of electric charge at all. Therefore, we assume that these wires (a) have no resistance (V œ 0), and that therefore (b) there is no change in potential Z at different positions along a wire (?Z œ 0 between any two points on the wire). In reality, metal wires do have some resistance, but it is quite small compared to the resistance of other circuit components. Therefore it is a very good approximation to neglect it, and to assume that V for a wire is zero. In this circuit, there is only one path for the charges to follow; each charge in the current flow must follow the same route. (Here, the charges flow out of the positive terminal of the battery, in to the left side of the resistor, out of the right side of the resistor, and then back in to the negative terminal of the battery.) A circuit with only one current path is called a series circuit. Now let's consider some questions about charges flowing in a current through this circuit. Question #1: A charge is moving around the circuit as part of current M . At point A, this charge has T I equal to B joules. When it returns to point A, having completed one circuit, is the T I of this charge greater than, less than, or equal to B joules? Answer: Equal to. Remember that the potential energy of a charge has a specific value for each different location. Whatever path that charge may take in traveling away from its initial position, when it returns to that position it must have exactly the same potential energy with which it started. (Here we are assuming that the source charges creating the electric field are not varying or moving; this will be the case if we have "steady" [unchanging] currents.) Let's consider what happens to the potential energy of that charge as it moves from point to point in the circuit. Question #2: Will the T I of the charge increase, decrease, or remain the same as it moves (a) from A to B; (b) from B to C; (c) from C to D. Answers: (a) remains the same; (b) decreases; (c) remains the same. To understand these answers, we might first substitute Z for T I and consider the same questions. As a charge moves along a wire segment for instance, from A to B, or from C to D its potential Z does not change (since the "perfectly conducting" wire segment is all at the same potential). Since ?T I œ ; ?Z and ?Z œ 0, we see that the potential energy of the charge does not vary as it moves through the wire. However, as discussed in the previous notes, the charge experiences a potential decrease as it flows through the resistor. Therefore, on the path from point B to point C, the charge's potential energy must also be decreasing. As we discussed earlier, the average kinetic energy of the charges flowing in the current is essentially constant. (The contribution to the kinetic energy made by their flow through the wire is also very small, since the average velocity of the charges in the direction of the current is only about 104 m/s!). So the total energy of the charges is decreasing. As the charges in the current flow through the resistor, they make many collisions with the atoms in the resistor. This makes these atoms vibrate, and in this way causes the resistor to get hot (and perhaps even give off light, if the resistor is actually the filament of a light bulb). So there is a transfer of energy from the charges in the current to the material in the resistor. In view of all of this, let us now ask: Question #3: As the charges flow from point D to point A, does their potential energy increase, decrease, or remain the same? Answer: Increase. In Question #1, we decided that the T I of the charges must return to the original value that it started out with at point A. Since the T I decreased as it went through the resistor, it must now increase as it goes through the battery. This makes sense, since we have already concluded that the battery must be supplying the energy to the charges that they are losing as they go through the resistor. Now, we can answer Question #4: Is the value of Z at point A higher, lower, or the same as the value of Z at point D? Answer: Higher. The positive charge gains potential energy as it goes from D to A, so it must be experiencing an increase in potential Z as well since ?Z œ ?T IÎ; . If ?T I 0 and ; 0, then ?Z must also be greater than zero. (Note that for a negative charge ; 0, and so an increase in T I implies a decrease in Z .) As we discussed in the previous notes, an ideal battery always maintains a constant, unchanging value of ?Z between its terminals. The battery uses chemical means to physically separate positive and negative charges, "pushing" them against the attractive forces that normally would bring them together. The result is that a battery creates a potential difference a ?Z within itself (and an electric field as well). In a sense, it "drags" a positive charge away from the negative terminal, pushes it toward the positive terminal, and then on through the wires away from the positive terminal. The forces involved in this "pushing" are chemical bonding forces. Finally, we may put all of these pieces together to find some general rule governing this type of circuit. Question #4: As a charge moves around a circuit in a complete loop, is the sum total of the increases in Z that it experiences along the way greater than, less than, or equal to the sum total of the decreases in Z that it experiences? Answer: Equal to. We know that the increases in T I must balance out the decreases in T I (since it returns to its original value of T I ); therefore, the same must be true for the increases and decreases in Z . We can now summarize the main points brought out in our notes that relate to the simple series circuit: 1. An ideal battery maintains a constant potential difference ?Z between its terminals. This potential difference ?Z is usually called the "battery voltage"; it is ?Z œ Z Z , where Z is the potential at the "positive" terminal, and Z is the potential at the "negative" terminal. By definition, the positive terminal is the one at the higher potential. (The positive terminal has an "excess" of positive charges, and creates a net electric field that pushes positive charges away from that terminal and on through the wire.) 2. As positive charges flow through a battery from the negative terminal to the positive terminal, their potential energy increases. There is a transfer of energy from the battery to the flowing current. 3. As positive charges flow through a resistor, their potential energy decreases, and so they flow from the side of the resistor at the higher potential to the side of the resistor at lower potential. The kinetic energy of the charges is essentially unchanged, and so their total energy decreases. There is a transfer of energy from the charges in the current to the material comprising the resistor. 4. Wires are made of conducting materials that offer very little resistance to the flow of current. We will always assume that wires are perfect conductors such that V œ 0, and so ?Z œ 0 between any two points on the wire. 5. The algebraic sum of the potential changes (increases minus decreases) experienced by charges as they go once around a full circuit is equal to zero. (The magnitude of [the sum of the increases] is equal to the magnitude of [the sum of the decreases].) QUESTIONS Prerequisite concepts: • In a series circuit, there is only one path for current to flow. • Battery "voltage" is the potential difference between the battery terminals. • Potential increases as current moves through battery from to terminal. • Algebraic sum of potential changes in a current loop equals zero. Questions #1 17 all refer to the circuit shown below: Question 1. Compared to the amount of current flowing through the 6-ohm resistor, the amount of current flowing through the 3-ohm resistor is: (1) half as much (2) the same (3) twice as much (4) can't be determined Question 2. Let's call the total amount of current flowing out of the battery Mtot . How does this quantity, Mtot , compare to the total amount of current flowing into the battery? (1) Mtot is larger (2) Mtot is the same (3) Mtot is smaller (4) can't be determined Question 3. Let's represent the amount of current flowing through the 6-ohm resistor by M6 , and that through the 3-ohm resistor by M3 . Which of the following numbered statements (I, II, III, and IV) is or are true? I. Mtot œ M3 (1) I only II. Mtot œ M6 (2) II only (3) III only III. Mtot œ M3 M6 IV. Mtot M3 M6 (4) IV only (6) None of them (5) I and II Question 4. What is the magnitude ?ZAE of the potential difference between points A and E? Remember that we assum all wires are ideal conductors. (1) ?ZAE œ 0 volts (2) 0 V ?ZAE 18 V (3) ?ZAE œ 18 volts (4) ?ZAE 18 volts (5) There isn't enough information to determine ?ZAE . Question 5. Which of the following statements is true? (1) The potential at B is the same as at D. (2) The potential at B is higher than that at D. (3) The potential at B is lower than that at D. (4) There isn't enough information to compare the potentials at B and D. Question 6. Which of the following statements is true? (1) A current of positive charges will flow through the resistors from point B to point D. (2) A current of positive charges will flow through the resistors from point D to point B. (3) There isn't enough information to determine the direction in which a current of positive charges would flow through the resistors. Question 7. Which of the following statements is true? (1) The potential at B is the same as at C. (2) The potential at B is higher than that at C. (3) The potential at B is lower than that at C. (4) There's not enough information to compare the potentials at B and C. Question 8. Which of the following statements is true? (1) The potential at C is the same as at D. (2) The potential at C is higher than that at D. (3) The potential at C is lower than that at D. (4) There's not enough information to compare the potentials at C and D. Question 9. Which of the following statements is true? (1) A current of positive charges will move through the battery from point E to point A. (2) A current of positive charges will move through the battery from point A to point E. (3) There isn't enough information to determine the direction in which positive charges would move through the battery. Question 10. Let ?ZBC œ lZB ZC l, that is, it is the magnitude of the potential difference between points B and C. Then ?Z3 œ ?ZBC , and is the magnitude of the potential change across the 3-ohm resistor. Similarly let ?ZCD œ lZC ZD l; then ?Z6 œ ?ZCD . Which of the following relationships is true? (1) ?Z3 œ 0.5 ?Z6 (4) none of the above (2) ?Z3 œ ?Z6 (3) ?Z3 œ 2 ?Z6 (5) not enought information to compare ?Z3 and ?Z6 Question 11. Let ?ZAB œ lZA ZB l and ?ZDE œ lZD ZE l. Which of the following relationships is correct? (1) (2) (3) (4) ?ZAE [?ZAB ?Z3 ?Z6 ?ZDE ] ?ZAE œ [?ZAB ?Z3 ?Z6 ?ZDE ] ?ZAE [?ZAB ?Z3 ?Z6 ?ZDE ] There is not enough information to determine the correct answer. Question 12. Assuming that the wires in the circuit are ideal conductors (remember what that means?), which of the following relationships is correct? (1) ?ZAB ?ZDE (4) ?ZAB œ ?ZDE œ 0 (2) ?ZAB ?ZDE (3) ?ZAB œ ?ZDE Á 0 (5) There is not enough information to decide. Question 13. Assuming that the wires in the circuit are ideal conductors, which of the following relationships is correct? (1) ?ZAE [?Z3 ?Z6 ] (2) ?ZAE œ [?Z3 ?Z6 ] (4) There is not enough information to decide. (3) ?ZAE [?Z3 ?Z6 ] Question 14. What is the electric current in this circuit? (1) 1 A (2) 1.5 A (3) 2 A (4) 3 A (5) 4 A (6) 6 A Question 15. What is the potential difference ?Z3 across the 3-ohm resistor? (1) 1 V (2) 2 V (3) 3 V (4) 4 V (5) 6 V (6) 12 V Question 16. What is the potential difference ?Z6 across the 6-ohm resistor? (1) 1 V (2) 2 V (3) 3 V (4) 4 V (5) 6 V (6) 12 V Question 17. If the electric potential at E is 0 volts, what is the electric potential at point C? (1) 12 V (2) 6 V (3) 0 V (4) 6 V (5) 12 V (6) 18 V Question 18. A battery is connected to a resistor; the current through the resistor is M . Which of these actions will result in the current increasing by a factor of four? (That is, M p 4M .) (1) (2) (3) (4) Double the battery voltage and double the resistance. Double the battery voltage and halve the resistance. Halve the battery voltage and double the resistance. Halve the battery voltage and halve the resistance. Question 19. A battery is connected to a resistor with resistance V ; the current through the resistor is M . If this same battery is connected to a different resistor with resistance 2V , what will be the current through this new resistor? (1) MÎ4 (2) MÎ2 (3) M (4) 2M (5) 4M Questions #20 22 refer to the figure at the right. Let ?ZR1 and ?ZR2 represent the magnitudes of the potential changes across resistors V1 and V2 , respectively. (These are also called the "voltage drops" across these resistors.) Assume that the potential at the negative terminal of the battery is 0 V, and let ZP represent the potential at point P. Question 20. If V2 œ V1 , find the following values: ?ZV1 œ ___________ ?ZV2 œ ___________ ZP œ ___________ Question 21. If V2 œ 2V1 , find the following values: ?ZV1 œ ___________ ?ZV2 œ ___________ ZP œ ___________ Question 22. If V2 œ 3V1 , find the following values: ?ZV1 œ ___________ ?ZV2 œ ___________ ZP œ ___________ Questions #23 32 all refer to this figure: Question 23. Rank, in order, using and œ , the following magnitudes: (1) (2) (3) (4) M4 , the amount of current flowing through the 4-ohm resistor. M6 , the amount of current flowing through the 6-ohm resistor. Mtot ß the amount of current flowing out of the battery. Min , the amount of current flowing into the battery. Ranking: (largest) ____________________________________ (smallest) Question 24. Rank, in order using and œ , the following magnitudes: (1) (2) (3) (4) (5) ?Z4 : the potential change across the 4-ohm resistor. ?Z6 : the potential change across the 6-ohm resistor. ?Zbat : the potential difference between the battery terminals. ?ZAB : the potential difference between point A and point B. ?ZDE : the potential difference between point D and point E. Ranking: (largest) ____________________________________ (smallest) Question 25. FInd the values of ?Z4 and ?Z6 by following this procedure: A. Write down the algebraic equation that relates the quantities ?Z4 , ?Z6 , and ?Zbat : B. Next, write down the algebraic equation that relates the quantities ?Z4 and ?Z6 to each other: C. Use the information on the diagram to determine the value of ?Zbat : ?Zbat œ ______. D. Put the value of ?Zbat into equation (A) and solve equations (A) and (B) for the values of ?Z4 and ?Z6 . ?Z4 œ ______________ ?Z6 œ ______________ Question 26. Determine the magnitudes of the following potential differences: ?ZAB œ _________________ ?ZBC œ _________________ ?ZCD œ _________________ ?ZDE œ _________________ ?ZAE œ _________________ Question 27. Assume that the potential at the negative terminal of the battery is 0 volts. Determine the potential at the following points: A: ________________________ B: ________________________ C: ________________________ D: ________________________ E: ________________________ Question 28. Determine the magnitude of the following potential differences: ?ZAC œ _________________ ?ZBE œ _________________ ?ZCE œ _________________ ?ZDA œ _________________ ?ZBD œ _________________ Question 29. The current flowing through the 4-ohm resistor is M4 œ ________________. The current flowing through the 6-ohm resistor is M6 œ ________________. Determine the current flowing past the following points on the circuit: A: ________________ B: ________________ D: ________________ E: ________________ C: ________________ Question 30. What is the "total current," the amount of current coming out of the battery? Mtotal œ ________________. What is the amount of current going into the battery? ________________ . Question 31. What is the ratio ?Zbat ÎMtot ? This is the equivalent resistance of the circuit: Veq œ Question 32. Let's represent the resistance of the 4-ohm resistor by V1 and the resistance of the 6-ohm resistor by V2 . What is a simple algebraic relationship involving V1 ß V2 ß and Veq ? Electrical Power How much energy is supplied by the battery each second? The whole idea behind constructing electrical circuits in the first place is to use electrical energy for some useful purpose, e.g. lighting a light bulb, turning a motor, heating a room, etc. Question: Identical light bulbs A and B are hooked up to batteries in different circuits. Given that PE transferred by the current to bulb A in the first circuit is 5 J, while PE transferred by the current in the second circuit to bulb B is 10 J, can one say that (a) bulb A is brighter than bulb B; (b) bulb B is brighter than bulb A; (c) bulbs A and B are the same brightness, or (d) there is not enough information to determine which is brighter. Answer: (d), there is not enough information. Suppose that the 5 J was supplied to bulb A in 0.01 s, while the 10 J was supplied to bulb B over a period of 10 s. Bulb A might burn brightly but very briefly just as if it were a flashbulb. Meantime, bulb B might not glow visibly at all. The rate of use of energy the ratio of [energy transferred Î elapsed time] is an important quantity when dealing with practical applications of electrical energy. This ratio is called power (symbol: T ). In the case of electrical currents, the OI of the charges is essentially constant, so we will use T œ ?T IÎ?>. The unit of power is called the watt (symbol: W). 1 W = 1 J/s. That is, one joule of energy supplied every second is equivalent to a power consumption of one watt (1 Ws = 1 J). A common unit of energy is the kilowatt-hour (kWh): 1 kWh is the amount of energy transferred when 1000 W of power is supplied for one hour. 1 kWh = 1000 Wh = 3.6 ‚ "06 J. Now, how can we figure out the power supplied by a battery in a particular circuit? First, let's consider the potential energy supplied by the battery to a particular quantity of charge call this quantity ?; as it flows through the battery from the negative terminal to the positive terminal. Then the change in potential energy of the charge will be given by ?T I œ Ð?;Ñ ‚ Ð?Z Ñ, where ?Z is the potential difference between the battery terminals. Then the power supplied by the battery is given by the following relationship: T œ ?T I ?> œ Ð?;ÑÐ?Z Ñ ?> œ ?; ?> Ð?Z Ñ œ M ?Z Here we have made use of the definition of electrical current, M œ ?;Î?>. So we can now see that the power supplied by the battery is equal to the [amount of current flowing through the battery] multiplied by the [battery voltage]. We will always use the symbol "Mtot " to refer to the amount of current flowing through the battery, and Tbat to refer to the power supplied by the battery. This gives us our first important relationship involving electrical power: Ê Tbat œ Mtot ?Zbat In the case of power "dissipated" by a resistor (that is, the rate of energy transfer by the current to the resistor), we know that there will be a loss of T I by the current as it flows through the resistor. By following the same line of reasoning as described above for the case of the battery, we can obtain a very similar relationship for power dissipated in a resistor with resistance V : Ê TR œ MR ?ZR This equation says that the power supplied to a particular resistor is given by the product of the current flowing through that resistor and the potential drop across that resistor. By using Ohm's law [MR œ ?ZR /MR ], we can obtain two other forms of that same relationship: Ê Ð1Ñ TR œ MR2 V (2) TR œ (?ZR Ñ2 V It is extremely important, when considering the power dissipated in a resistor, to use the M , V , and the ?Z for that particular resistor only, and not, for instance, the values referring to the battery, or to some other resistor. These last two equations can only be applied to the power supplied by the battery when the quantity Veq is used for the resistance. (The equivalent resistance Veq will be discussed in more detail later). In that case we will have the following relationships: Ê 2 Ð1Ñ Tbat œ Mtot Veq (2) Tbat œ QUESTIONS (?Zbat Ñ2 Veq Parallel Circuits When current flows along more than one path, how does it get divided up? So far, we have considered circuits in which the current flowed along only a single path. The charges never "had a choice" about where to go. However, most circuits are a lot more complicated than that. There are multiple paths along which charge may flow, and the geometrical layout of the circuit can get very complex. A location at which current may branch off into two or more different paths is called a junction. There is a simple and important rule that governs the behavior of current at such a junction. It is called Kirchoff's Junction Rule: The total current flowing into a junction equals the total current flowing out of that same junction. The explanation for this rule is also simple: if the current flowing out were less than the current flowing in, that would mean that charges were getting trapped in the junction. Eventually (and actually, very very quickly) the pileup of charge would cause a meltdown in the junction. If, on the other hand, the current flowing out were more than the current flowing in, that would mean that there was some external source of charge putting extra charges into the junction. We assume that that never happens. So for instance, for the diagram shown here, we have the relationship M1 œ M 2 M 3 . Now we can examine the simplest circuit in which current can flow along more than one path: a two-resistor parallel circuit. (It's called a parallel circuit because of the geometry of the circuit diagram.) In this circuit, current flows out of the battery from the positive terminal, and then divides at point A. Part of the current goes through V1 , and part flows through V2 . Then, at point D, the current combines again. Let's assume that V2 = 2V1 , and answer these questions. Question 1 À What is the ranking of the potential at the points A, B, C, D and E? Answer: ZA œ ZB ZC œ ZD œ ZE . Points A and B are connected by "perfectly conducting" wires to the positive terminal of the battery, so the potential at those points must be the same as that at the positive terminal. Similarly, points C, D, and E are connected to the negative terminal of the battery, and so must all be at the same potential. (We will always assume that the negative terminal of the battery is at a potential of zero volts.) Question 2: What is the relationship between M" (the current flowing through resistor V1 ) and M2 (the current flowing through resistor V2 )? Answer: First we need to realize that ?Z" œ ?Z2 œ ?Zbat . This is because all three of those potential differences are equal to ?ZAD œ ZA ZD , which we could figure out from the ranking of potentials given above. Now, we know that M1 œ ?Z1 ÎV1 . Also, we can see that M2 œ ?Z2 ÎV2 œ ?Z1 ÎV2 œ ?Z1 Î2V1 = ½ ?Z1 ÎV1 œ ½ M1 . So our final result is that M2 œ ½ M1 . More current flows through the smaller resistor. Question 3: What is the ranking of the current flowing past points B, C and E? Answer: ME MB MC . All of the current that is, Mtot must flow through point E. The amount flowing past point B is the same as the amount flowing through resistor V1 (i.e., M1 ) while that flowing past point C is the same as M2 . Finally, we need to give a definition of "equivalent resistance," symbolized by Veq . The equivalent resistance is like an imaginary "substitute" resistor that replaces all of the resistors in a particular circuit. We can imagine putting all of the resistors in a circuit with all of their complicated connections, which may combine both series and parallel connections in a closed "black box" Ð"bb"Ñß with one wire going in, and one wire going out. When we hook up that black box to a battery, we get a certain amount of current flowing out of the battery, which we call Mtot . Mtot œ ?Zbat ÎVbb . Then we see that Vbb œ ?Zbat ÎMtot . Suppose we want to take away that black box with all of its complicated connections, and replace it with one single resistor but we want to use the same battery, and get the same Mtot as before. Then that single resistor should have a resistance equal to Veq , where we choose Veq so that we get the same current as we did with the black box. Therefore, for any circuit, Veq œ ?Zbat ÎMtot . 8. What is the magnitude of the electric potential at point B? (A) 0 V (B) 3 V (C) 4 V (D) 6 V (E) 8 V (F) 12 V 9. What is the magnitude of the electric potential at point C? (A) 0 V (B) 3 V (C) 4 V (D) 6 V (E) 8 V (F) 12 V 10. What is the magnitude of the electric potential at point D? (A) 0 V (B) 3 V (C) 4 V (D) 6 V (E) 8 V (F) 12 V 11. What is the magnitude of the current flow through the 4 H resistor? (A) 3 A (B) 4 A (C) 6 A (D) 8 A (E) 9 A (F) 10 A 12. What is the magnitude of the current flow through the 2 H resistor? (A) 3 A (B) 4 A (C) 6 A (D) 8 A (E) 9 A (F) 10 A 13. What is the magnitude of the current flow through point B? (A) 3 A (B) 4 A (C) 6 A (D) 8 A (E) 9 A (F) 10 A 14. What is the magnitude of the current flow through point D? (A) 3 A (B) 4 A (C) 6 A (D) 8 A (E) 9 A (F) 10 A (D) 8 A (E) 9 A (F) 10 A 15. What is the magnitude of Mtot ? (A) 3 A (B) 4 A (C) 6 A V M ?Z T TABLES A useful way to organize and check information about circuits is by using an V M ?Z T table. It consists of four columns labeled V , M , ?Z , and T , and can be used for series, parallel, and more complex circuits. The entries in the last two columns (?Z and T ) are each the product of the entries of the two previous columns in the same row. Each row corresponds to either a particular resistor or a particular battery. SERIES CIRCUIT: The simplest series circuits have one battery Ðwith potential difference ?Zbat Ñ and one or more resistors connected in series, so that there is a single electric current Mtotal passing throught the battery and each resistor. The equivalent resistance Veq œ sum of all the resistances in the series circuit. Mtotal œ Ð?Zbat ÑÎVeq . V V" V2 =?7 œ Veq M Mtotal Mtotal =+7/ œ Mtotal ?Z œ V ‚ M =?7 œ ?Zbat œ V eq ‚ Mtotal T œ M ‚ ?Z =?7 œ Mtotal ‚ ?Zbat Note: (1) the sum of the resistances can be entered on the battery row as Veq ; (2) the entries in the current column are all the same; (3) the sum of the ?Z for the resistors must equal ?Zbat ; (4) the sum of the powers dissipated by the resistors must equal the power supplied by the battery. If there are several batteries in the series circuits: (1) provide a row for each battery, entering its ?Z as negative if the current passes through it in the "wrong" direction (from positive terminal to negative terminal); (2) leave the resistance column entries for the batteries blank; (3) the power column entries are positive if the battery is supplying power and negative if the battery is actually charging rather than discharging. In this case ?Zbat is the algebraic sum of the ?Z values for the different batteries, and must equal the sum of the ?Z values for the resistors; also, the electric currents are all the same and the sum of the powers dissipated by the resistors equals the algebraic sum of the powers supplied by the batteries. PARALLEL CIRCUIT: The simplest parallel circuit has one battery (of potential difference ?Zbat ) and one or more resistors in parallel with it. Every parallel circuit has the same potential difference across each resistor. V V" V2 Veq œ "ÎÒ1ÎV1 1ÎV2 Ó M M1 M2 =?7 œ Mtotal ?Z œ V ‚ M ?Zbat ?Zbat =a7e œ ?Zbat œ V eq ‚ Mtotal T œ M ‚ ?Z =?7 œ Mtotal ‚ ?Zbat COMPLEX CIRCUITS: For more complex circuits, such as circuits with combinations of series and parallel branches, a table can be prepared for each resistor and each battery. The "sum" and "same" rules above still apply for parts of the circuit, for which subtables can be prepared. Very complex circuits with many branches, resistors, and batteries can be analyzed using Kirchhoff's laws: (1) The algebraic sum of the currents coming into a junction must add up to zero; (2) the sum of the potential differences around any closed path in the circuit must be zero. EXAMPLES EXAMPLE 1: A simple series circuit consisting of one battery and one resistor. Let's suppose this circuit has a single battery with a potential difference ?Zbat œ 12 V in series with a single resistor of resistance V œ 4 H. In filling out the V M ?Z T table for this circuit we begin with two rows, one for the resistor and one for the battery. First, we fill in the V column for the resistor with "4 H" and the ?Z column for the battery with "12 V." Next, in the V column for the battery we enter the equivalent resistance Veq œ sum of resistors œ 4 H. Next, we determine the current through the battery by taking M œ ?Z ÎV œ Ð12 VÑÎÐ4 HÑ œ 3 A. Since every element in a series circuit has the same current, we also enter this current in the M column for the resistance. Next, we determine the ?Z for the resistor: ?Z œ VM œ Ð4 HÑÐ3 AÑ œ 12 V. We can then finish by calculating the power T dissipated by the resistor as T œ M ?Z œ Ð3 AÑÐ12 VÑ œ 36 W and the power supplied by the battery as T œ M ?Z œ Ð3 AÑÐ12 VÑ œ 36 W. Here is the completed table: V 4H 4H M 3A 3A ?Z œ V ‚ M 12 V 12 V T œ M ‚ ?Z 36 W 36 W EXAMPLE 2: A series circuit consisting of one battery and three resistors. In this case let's suppose there is a single battery Ð?Zbat œ 12 VÑ in series with three resistors of resistances 1 H, 2 H, and 3 H, respectively. Our V M ?Z T table has four numerical rows, one each for the battery and each of the three resistors. Check the values in the table shown. The strategy is (1) determine V eq, (2) determine M for the battery, (3) enter the same current for each resistor, (4) determine the ?Z for each resistor and the T for each resistor and the battery. Finally, check that the sum of the ?Z values for the three resistors equals ?Zbat and that the sum of the powers dissipated by the three resistors equals the power supplied by the battery. Here is the completed table. V 1H 2H 3H 6H M 2A 2A 2A 2A ?Z œ V ‚ M 2V 4V 6V 12 V T œ M ‚ ?Z 4W 8W 12 W 24 W EXAMPLE 3: A parallel circuit consisting of one battery and three resistors in parallel with that battery. In this case let's suppose there is a single battery Ð?Zbat œ 12 VÑ in series with three resistors of resistances 1 H, 2 H, and 3 H, respectively. Our V M ?Z T table has four numerical rows, one each for the battery and each of the three resistors. Check the values in the table shown. The strategy is (1) recognize that each resistor has the same ?Z as the battery, and enter these in the ?Z table; (2) determine M for each resistor; (3) add up the three currents and enter the sum as the current through the battery; (4) determine the equivalent resistance of the circuit by dividing the ?Z for each the battery by its total current; (5) determine the T for each resistor and the battery. Finally, check that the sum of the powers dissipated by the three resistors equals the power supplied by the battery. Another check is to use the formula for the equivalent resistance of a parallel circuit and check that this is what you have in the bottom left-hand entry in the table. Here is the completed table. V 1H 2H 3H 6/11 H M 12 A 6A 4A 22 A ?Z œ V ‚ M 12 V 12 V 12 V 12 V T œ M ‚ ?Z 144 W 72 W 48 W 264 W Checking the powers, we note that 144 W 72 W 48 W œ 264 W, the same as the entry for the power supplied by the battery. Checking the equivalent resistance of the parallel circuit, 1ÎVeq œ 1Î1 H 1Î2 H "Î$ H œ Ð' 3 2)Î6 H œ 11Î6 H so Veq œ 6Î11 H, which is correct. EXAMPLE 4: A complex circuit with two batteries in series with a resistor and a parallel combination of two other resistors. Look a the circuit shown above. There are two batteries facing in different directions in the circuit. One has a potential difference of 27 V and the other 9 V. They are in series with a 4-H resistor and a parallel combination of a 3-H resistor with a 6-H resistor. The steps in solving this circuit and filling in the values in the table are: (1) First we note that the equivalent "voltage" of the circuit is 27 V 9 V œ 18 V. We have to subtract the potential difference of the smaller battery in this case because it faces in the opposite direction as we trace our way across the circuit in either direction. In the table we enter lines for each battery, and give their ?Z values as 27 V and 9 V, respectively. We can tell that the electric current will flow to the left through the batteries and the 4-ohm resistor, and to the right through the 3-ohm and 6-ohm resistors. (2) Next we determine the equivalent resistance of the whole circuit. We must first determine the equivalent resistance of the parallel combination. This can be calculated as 1ÎVeq œ 1Î3 H 1Î6 H œ Ð2 1)Î6 H œ 3Î6 H œ 1/2 H so Veq œ 2 H. Now we can determine the equivalent resistance of the whole circuit by adding the resistances in series: Veq œ 4 H 2 H œ 6 H (3) The current passing through the batteries is found by dividing the equivalent potential difference of the batteries, 18 V, by the equivalent resistance of the whole circuit, 6 H, to give 3 A. This can be entered in the table as the current through each battery and through the 4-H resistor. (4) The ?Z across the 4-H resistor is then ?Z œ MV œ Ð3 AÑÐ4 HÑ œ 12 V. (5) Since the equivalent ?Z of the batteries is 18 V, that means 18 V 12 V œ 6 V must appear across the parallel combination, so we can enter ?Z œ 6 V for both the 3-H resistor and the 6-H resistor. (6) We can now determine the currents across the 3-H resistor as M œ ?Z ÎV œ Ð6 VÑÎÐ3 HÑ œ 2 A and across the 6-H resistor as M œ ?Z ÎV œ Ð6 VÑÎÐ6 HÑ œ 1 A. We can check that the sum of these currents is 3 A, same as the current through the rest of the circuit. (7) We can now fill in the values of the powers. If we check the powers dissipated in the three resistors we have 36 W 12 W 6 W œ 54 W, same as the algebraic sum of the powers supplied by the two batteries: 27 W 81 W œ 54 W. In effect, the 81 W supplied by the 27-V battery supplies the 54 W dissipated by the three resistors plus 27 W used to recharge the 9-V battery facing in the opposite direction. Here is the completed table. Note that no equivalent resistances are entered for the batteries. V 4H 3H 6H M 3A 2A 1A 3A 3A ?Z œ V ‚ M 12 V 6V 6V 9V 27 V T œ M ‚ ?Z 36 W 12 W 6W 27 W 81 W