Download Example (cont)

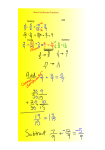
Objectives
 Solve
systems of linear equations in three variables
using left-to-right elimination
 Find solutions of dependent systems
 Determine when a system of equations is inconsistent
Operations on a System of Equations
The following operations result in an equivalent system.
1. Interchange any two equations.
2. Multiply both sides of any equation by the same
nonzero number.
3. Multiply any equation by a number, add the result to a
second equation, and then replace the second
equation with the sum.
Left-to-Right Elimination Method of Solving Systems
of Linear Equations in Three Variables x, y, and z
1. If necessary, interchange two equations or use
multiplication to make the coefficient of x in the first
equation a 1.
2. Add a multiple of the first equation to each of the
following equations so that the coefficients of x in the
second and third equations become 0.
3. Multiply (or divide) both sides of the second equation
by a number that makes the coefficient of y in the
second equation equal to 1.
4. Add a multiple of the (new) second equation to the
(new) third equation so that the coefficient of y in the
newest third equation becomes 0.
Left-to-Right Elimination Method of Solving Systems
of Linear Equations in Three Variables x, y, and z
5. Multiply (or divide) both sides of the third equation by
a number that makes the coefficient of z in the third
equation equal to 1. This gives the solution for z in the
system of equations.
6. Use the solution for z to solve for y in the second
equation. Then substitute values for y and z to solve
for x in the first equation. (This is called back
substitution.)
Example
2
x

3
y

z


1

Solve the system 
 x  y  2 z  3
3 x  y  z  9

 x  y  2 z  3
Solution

Interchange equations 1 and 2. 2 x  3 y  z  1
3 x  y  z  9

Multiply equation 1 by –2 and
add it to the second equation.
Multiply equation 1 by –3 and
add it to the second equation.
 x  y  2 z  3

 y  3z  5
4 y  7z  18

Example (cont)
To get 1 as the coefficient of
y of the second equation multiply
by 1.
Multiply equation 2 by –4 and
add it to the third equation.
Solve for z.
 x  y  2 z  3

 y  3 z  5
4 y  7z  18

 x  y  2 z  3

 y  3 z  5
19z  38

 x  y  2 z  3

 y  3 z  5
z  2

Example (cont)
Substituting z = 2 for z in the
second equation and solving for
y gives y + 3(2) = 5, so y = 1.
 x  y  2 z  3

 y  3 z  5
z  2

Substituting z = 2 and y = 1 in the first equation and
solving for x gives x – 1 + 2(2)) = 3, so x = 2.
The solution is (2, 1, 2).
Example
A manufacturer of furniture has three models of chairs:
Anderson, Blake, and Colonial. The numbers of hours
required for framing, upholstery, and finishing for each
type of chair are given in the table. The company has
1500 hours per week for framing, 2100 hours for
upholstery, and 850 hours for finishing. How many of
each type of chair can be produced under these
conditions?
Example (cont)
Let x represent Anderson
Let y represent Blake
Let z represent Colonial
Framing: 2x + 3y + z = 1500
Upholstery: x + 2y + 3z = 2100
Finishing: x + 2y + 0.5z= 850
Interchange equations 1 and 2.
 x  2y  3z  2100

2 x  3 y  z  1500
 x  2y  0.5z  850

Example (cont)
(2)Eq1 + Eq2
(1)Eq1 + Eq3  x  2y  3z  2100

 y  5z  2700


2.5z  1250

Solve for z.
2.5z  1250
z  500
Solve for y.
 y  5(500)  2700
y  200
Example (cont)
Solve for x.
x  2(200)  3(500)  2100
x  200
Thus, 200 Anderson, 200 Blake, and 500 Colonial chairs
should be made under the given conditions.
Nonunique Solutions
It is not always possible to reduce a system of three
equations in three variables to a system in which the third
equation contains one variable.
A system in which 0 = x (any number) is inconsistent.
A system in which 0 = 0 is a dependent system.
Example
Solve the system.  x  y  4z  5

3 x  z  0
 x  y  4z  20

(3) Eq1 + Eq 2
Eq(1) + Eq(3)
 x  y  4z  5

 3 y  11z  15

0  15

0 = 15 is impossible. The
system is inconsistent and has
no solution.
Example
Solve the system.  x  y  2z  0

 x  2y  z  6
2 x  y  z  6

(1) Eq1
 x  y  2z  0

 x  2y  z  6
2 x  y  z  6

(1)Eq1+ Eq2
(2)Eq1 + Eq3
 x  y  2z  0

 3 y  3z  6
 3 y  3z  6

Example (cont)
 x  y  2z  0

 3 y  3z  6
 3 y  3z  6

(1/3)Eq2
 x  y  2z  0

y z2

 3 y  3z  6

  x  y  2z  0

 x  2y  z  6
2 x  y  z  6

Eq2 + Eq3
 x  y  2z  0

y z2


00

The equation has infinitely many solutions.
z = any number; y = 2 – z and x = 2 + z
Assignment
Pg. 505-508
#1-25 odd
#27, 31, 34,