* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download chapter28
Schmitt trigger wikipedia , lookup
Integrated circuit wikipedia , lookup
Lumped element model wikipedia , lookup
Index of electronics articles wikipedia , lookup
Regenerative circuit wikipedia , lookup
Power electronics wikipedia , lookup
Negative resistance wikipedia , lookup
Electric battery wikipedia , lookup
Operational amplifier wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Surge protector wikipedia , lookup
Power MOSFET wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Battery charger wikipedia , lookup
Opto-isolator wikipedia , lookup
Rechargeable battery wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Two-port network wikipedia , lookup
Electrical ballast wikipedia , lookup
Current mirror wikipedia , lookup
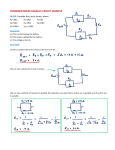
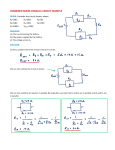
Current source wikipedia , lookup
RLC circuit wikipedia , lookup
Chapter 28 Direct Current Circuits 1 Direct Current When the current in a circuit has a constant direction, the current is called direct current Most of the circuits analyzed will be assumed to be in steady state, with constant magnitude and direction Because the potential difference between the terminals of a battery is constant, the battery produces direct current The battery is known as a source of emf 2 Electromotive Force The electromotive force (emf), e, of a battery is the maximum possible voltage that the battery can provide between its terminals The emf supplies energy, it does not apply a force The battery will normally be the source of energy in the circuit The positive terminal of the battery is at a higher potential than the negative terminal We consider the wires to have no resistance 3 Internal Battery Resistance If the internal resistance is zero, the terminal voltage equals the emf In a real battery, there is internal resistance, r The terminal voltage, DV = e – Ir 4 EMF, cont The emf is equivalent to the open-circuit voltage This is the terminal voltage when no current is in the circuit This is the voltage labeled on the battery The actual potential difference between the terminals of the battery depends on the current in the circuit 5 Load Resistance The terminal voltage also equals the voltage across the external resistance This external resistor is called the load resistance In the previous circuit, the load resistance is just the external resistor In general, the load resistance could be any electrical device These resistances represent loads on the battery since it supplies the energy to operate the device containing the resistance 6 Power The total power output of the battery is I DV Ie This power is delivered to the external resistor (I 2 R) and to the internal resistor (I2 r) I R I r 2 2 7 Example 28.1 Terminal Voltage of a Battery A battery has an emf of 12V and an internal resistance of 0.05 Its terminals are connected to a load resistance of 3 Find the current in the circuit and the terminal voltage of the battery Calculate the power delivered to the load resistor, the power delivered to the internal resistance of the battery and the power delivered by the battery 8 Example 28.1 Terminal Voltage of a Battery Find the current in the circuit and the terminal voltage of the battery e 12V I 3.93 A R r (3 0.05) DV e Ir 12V (3.93 A)(0.05) 11.8V 9 Example 28.1 Terminal Voltage of a Battery Calculate the power delivered to the load resistor, the power delivered to the internal resistance of the battery and the power delivered by the battery PR I 2 R (3.93 A) 2 (3) 46.3W load resistor 2 2 P I r ( 3 . 93 A ) (0.05) 0.772W Internal r battery P PR Pr 46.3W 0.772W 47.1W 10 Example 28.2 Matching the Load Find the load resistance R for which the maximum power is delivered to the load resistance e e PR I R R Rr Rr 2 dPR d e R 0 dR dR R r 2 e (r R) 0 Rr 3 (R r) I 2 2 11 Resistors in Series When two or more resistors are connected end-toend, they are said to be in series For a series combination of resistors, the currents are the same in all the resistors because the amount of charge that passes through one resistor must also pass through the other resistors in the same time interval The potential difference will divide among the resistors such that the sum of the potential differences across the resistors is equal to the total potential difference across the combination 12 Resistors in Series, cont Potentials add ΔV = IR1 + IR2 = I (R1+R2) Consequence of Conservation of Energy The equivalent resistance has the same effect on the circuit as the original combination of resistors 13 Resistors in Series – Example Observe the effect on the currents and voltages of the individual resistors 14 Equivalent Resistance – Series Req = R1 + R2 + R3 + … The equivalent resistance of a series combination of resistors is the algebraic sum of the individual resistances and is always greater than any individual resistance If one device in the series circuit creates an open circuit, all devices are inoperative 15 Equivalent Resistance – Series – An Example Two resistors are replaced with their equivalent resistance 16 Some Circuit Notes A local change in one part of a circuit may result in a global change throughout the circuit For example, changing one resistor will affect the currents and voltages in all the other resistors and the terminal voltage of the battery In a series circuit, there is one path for the current to take In a parallel circuit, there are multiple paths for the current to take 17 Resistors in Parallel The potential difference across each resistor is the same because each is connected directly across the battery terminals A junction is a point where the current can split The current, I, that enters a point must be equal to the total current leaving that point I=I1+I2 The currents are generally not the same Consequence of Conservation of Charge 18 Equivalent Resistance – Parallel, Examples Equivalent resistance replaces the two original resistances I I1 I 2 DV I Req DV DV1 DV2 DV2 DV1 I2 I1 R2 R1 1 1 1 Req R1 R2 19 Equivalent Resistance – Parallel Equivalent Resistance 1 1 1 1 Req R1 R2 R3 The inverse of the equivalent resistance of two or more resistors connected in parallel is the algebraic sum of the inverses of the individual resistance The equivalent is always less than the smallest resistor in the group 20 Resistors in Parallel – Example Observe the effect on the currents and voltages of the individual resistors 21 Resistors in Parallel, Final In parallel, each device operates independently of the others so that if one is switched off, the others remain on In parallel, all of the devices operate on the same voltage The current takes all the paths The lower resistance will have higher currents Even very high resistances will have some currents Household circuits are wired so that electrical devices are connected in parallel 22 Example 28.4 Combinations of Resistors The 8.0- and 4.0- resistors are in series and can be replaced with their equivalent, 12.0 The 6.0- and 3.0- resistors are in parallel and can be replaced with their equivalent, 2.0 These equivalent resistances are in series and can be replaced with their equivalent resistance, 14.0 23 Example 28.4 Combinations of Resistors What is the current in each resistor if a potential difference of 42V is maintained between a and c? I I1 I 2 42V I 14 I 3 A DVbc I1 6 I 2 3 I 2 2I1 I1 1A I 2 2 A 24 Example 28.5 Three Resistors in Parallel Three resistors are connected in parallel A potential difference of 18V is maintained between points a and b Calculated the equivalent resistance of the circuit Find the current in each resistor Calculate the power delivered to each resistor and the total power delivered to the combination of resistors. 25 Example 28.5 Three Resistors in Parallel Calculated the equivalent resistance of the circuit 1 1 1 1 1 1 1 Req R1 R2 R3 3 6 9 18 Req 11 Find the current in each resistor DV 18V I1 6A R1 3 DV 18V I2 3A R2 6 I3 2 A 26 Example 28.5 Three Resistors in Parallel • Calculate the power delivered to each resistor and the total power delivered to the combination of resistors. P1 I12 R1 P2 I 22 R2 P3 I R3 2 3 27 Gustav Kirchhoff 1824 – 1887 German physicist Worked with Robert Bunsen They Invented the spectroscope and founded the science of spectroscopy Discovered the elements cesium and rubidium Invented astronomical spectroscopy 28 Kirchhoff’s Rules There are ways in which resistors can be connected so that the circuits formed cannot be reduced to a single equivalent resistor Two rules, called Kirchhoff’s rules, can be used instead 29 Kirchhoff’s Junction Rule Junction Rule The sum of the currents at any junction must equal zero Currents directed into the junction are entered into the -equation as +I and those leaving as -I A statement of Conservation of Charge Mathematically, I 0 junction 30 More about the Junction Rule I1 - I2 - I3 = 0 Required by Conservation of Charge Diagram (b) shows a mechanical analog 31 Kirchhoff’s Loop Rule Loop Rule The sum of the potential differences across all elements around any closed circuit loop must be zero A statement of Conservation of Energy Mathematically, DV 0 closed loop 32 More about the Loop Rule Traveling around the loop from a to b In (a), the resistor is traversed in the direction of the current, the potential across the resistor is – IR In (b), the resistor is traversed in the direction opposite of the current, the potential across the resistor is is + IR 33 Loop Rule, final In (c), the source of emf is traversed in the direction of the emf (from – to +), and the change in the electric potential is +ε In (d), the source of emf is traversed in the direction opposite of the emf (from + to -), and the change in the electric potential is -ε 34 Junction Equations from Kirchhoff’s Rules Use the junction rule as often as needed, so long as each time you write an equation, you include in it a current that has not been used in a previous junction rule equation In general, the number of times the junction rule can be used is one fewer than the number of junction points in the circuit 35 Loop Equations from Kirchhoff’s Rules The loop rule can be used as often as needed so long as a new circuit element (resistor or battery) or a new current appears in each new equation You need as many independent equations as you have unknowns 36 Kirchhoff’s Rules Equations, final In order to solve a particular circuit problem, the number of independent equations you need to obtain from the two rules equals the number of unknown currents Any capacitor acts as an open branch in a circuit The current in the branch containing the capacitor is zero under steady-state conditions 37 Example 28.6 A Single-Loop Circuit A single-loop circuit contains two resistors and two batteries Find the current in the circuit Kirchhoff’s loop rule: Starting from a, e1 IR1 e 2 IR2 0 6V 8I 12V 10 I 0 I 0.33 A 38 Example 28.7 A Multiloop Circuit Find the current in the circuit Junction rule at junction c: I1 I 2 I 3 0 Loop rule for abcda: 10V (6) I1 (2) I 3 0 Loop rule for befcb: (4)I 2 14V (6) I1 0 Solve I1, I2, and I3! 39 RC Circuits In direct current circuit containing capacitors, the current may vary with time The current is still in the same direction An RC circuit will contain a series combination of a resistor and a capacitor 40 Charging a Capacitor When the circuit is completed, the capacitor starts to charge The capacitor continues to charge until it reaches its maximum charge (Q = Cε) Once the capacitor is fully charged, the current in the circuit is zero 41 Charging a Capacitor Kirchhoff’s loop rule: q e IR 0 C e Initially, I i Finally, Q Ce dq e q I dt R CR R 42 Charging a Capacitor dq e q I dt R CR q t dq dt dq q Ce q Ce RC dt RC 0 0 t q Ce ln RC Ce q(t) = Ce(1 – e-t/RC) = Q(1 – e-t/RC) ε t RC I( t ) e R Time constant =RC 43 Charging an RC Circuit, cont. As the plates are being charged, the potential difference across the capacitor increases At the instant the switch is closed, the charge on the capacitor is zero Once the maximum charge is reached, the current in the circuit is zero The potential difference across the capacitor matches that supplied by the battery 44 Charging a Capacitor in an RC Circuit The charge on the capacitor varies with time q(t) = Ce(1 – e-t/RC) = Q(1 – e-t/RC) The current can be found ε t RC I( t ) e R is the time constant = RC 45 Time Constant, Charging The time constant represents the time required for the charge to increase from zero to 63.2% of its maximum has units of time The energy stored in the charged capacitor is ½ Qe = ½ Ce2 46 Discharging a Capacitor Kirchhoff’s loop rule: q IR 0 C dq q I dt CR q t dq dt Q q 0 RC q(t) = Qe-t/RC dq Q t RC I t e dt RC 47 Discharging a Capacitor in an RC Circuit When a charged capacitor is placed in the circuit, it can be discharged q(t) = Qe-t/RC The charge decreases exponentially 48 Discharging Capacitor At t = = RC, the charge decreases to 0.368 Qmax In other words, in one time constant, the capacitor loses 63.2% of its initial charge The current can be found dq Q t RC I t e dt RC Both charge and current decay exponentially at a rate characterized by = RC 49 Example 28.9 Charging a Capacitor in an RC Circuit An uncharged capacitor and a resistor are connected in series to a battery where e=12V, C=5F, and R=8105 The switch is thrown to position a Find the time constant of the circuit, the maximum charge on the capacitor, the maximum current, and the charge and current as functions of time 50 Example 28.9 Charging a Capacitor in an RC Circuit e=12V, C=5F, and R=8105 time constant: =RC= 8105510-6 =4s the maximum charge on the capacitor: Q=Ce= 5F 12V =60 C the maximum current: Ii= e/R=12V/8105=15 A 51 Example 28.10 Discharging a Capacitor in an RC Circuit Consider a capacitor of capacitance C that is being discharged through a resistor of resistance R After how many time constants is the charge on the capacitor one-fourth its initial value? Q Qe t / RC 4 t RC ln 4 ln 4 52 Example 28.10 Discharging a Capacitor in an RC Circuit The energy stored in the capacitor decreases with time as the capacitor discharges After how many time constants is this stored energy one-fourth its initial value? Equation 26.11 and 28.18: q 2 Q 2 2t / RC U (t ) e 2C 2C 1 ln 4 1 Q 2 Q 2 2t / RC t RC ln 4 e 2 2 4 2C 2C 53 Example 28.11 Energy Delivered to a Resistor A 5-F capacitor is charged to a potential difference of 800V and then discharged through a resistor How much energy is delivered to the resistor in the time interval required to fully discharge the capacitor? Energy types: Electric potential and internal energy 1 2 DU+Eint=0 E R U C Ce 2 Solve ER! 54