Download Points

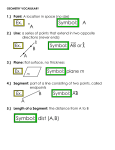
Points
We may think of a point as a "dot" on a piece of paper or the pinpoint on a
board. In geometry we usually identify this point with a number or letter. A
point has no length, width, or height - it just specifies an exact location. It
is zero-dimensional.
The following is a diagram of points A, B, and M:
Lines
A line is one-dimensional. That is, a line has length, but no width or height. In
geometry, a line extends forever in both directions. A line is uniquely
determined by two points.
The line passing through the points A and B
is denoted by
Colinear points are points on the same line.
The following is a diagram of two lines: line AB and line HG.
1
Planes
Planes are two-dimensional. A plane has length and width, but no height, and
extends infinitely on all sides. Planes are thought of as flat surfaces, like a
tabletop. A plane is made up of an infinite amount of lines. Two-dimensional
figures are called plane figures.
*A
*B
R
Plane R
Points A and B are coplanar.
Intersection
The term intersect is used when lines, rays, line segments or figures
meet, that is, they share a common point. The point they share is
called the point of intersection. We say that these figures intersect.
Example: In the diagram below, line AB and line GH intersect at point
D:
Space
Space is the set of all points in the three dimensions - length, width
and height. It is made up of an infinite number of planes. Figures in
space are called solids.
2
Figures in
space
Line Segments
A line segment is one of the basic terms in geometry. We may think of
a line segment as a "straight" line that we might draw with a ruler on a
piece of paper. A line segment does not extend forever, but has two
distinct endpoints. We write the name of a line segment with
endpoints A and B as "line segment AB" or as
. Note how there are
no arrow heads on the line over AB such as when we denote a line or a
ray.
Example: The following is a diagram of two line segments: line segment
CD and line segment PN, or simply segment CD and segment PN.
Rays
A ray is one of the basic terms in geometry. We may think of a ray as
a "straight" line that begins at a certain point and extends forever in
one direction. The point where the ray begins is known as its endpoint.
We write the name of a ray with endpoint A and passing through a
point B as "ray AB" or as
. Note how the arrow heads denotes the
3
direction the ray extends in: there is no arrow head over the endpoint.
Example: The following is a diagram of two rays: ray HG and ray AB.
Endpoints
An endpoint is a point used to define a line segment or ray. A line
segment has two endpoints; a ray has one.
Example: The endpoints of line segment DC below are points D and C,
and the endpoint of ray MN is point M below:
PQ  PM  MQ
line segment PQ
PM  QR
4
9/11/09
Coordinate Plane
Made up of two axes, X-axis and Y-axis. The center of the coordinate plane
is the origin (0,0). Coordinate points are called an ordered pair.
To determine the distance of a segment, take the absolute value of the
subtraction of 2 endpoints.
Ex.
-7 -6 -5
-4
-3 -2 -1 0 1 2 3 4
5 6 7
|-4-6|=|-10|= 10
(2,8)
(7,3)
5
Distance Formula
D=
Ex. D=
( x 2  x1 ) 2  ( y 2  y1 )
D=
(7  2) 2  (3  8) 2
52  52
D = 25  25
D=
50 = 7.07
9/14/09
Sides that are equal are congruent.
Finding the Midpoint of a Segment
(-4,5)
(3,5)
Midpoint Formula: Remember the midpoint is a point (x,y)
M= (
x1  x2 y1  y 2
43 55
 1 10
,
) =(
) = ( , ) = (-.5,5)
,
2
2
2 2
2
2
The midpoint of the line segment is (-.5,5)
9/17/09
Angles and Rays
A ray has an endpoint and a direction. Ray AB
A
B
An angle is made up of 2 sides that are rays with a common endpoint.
Angle A
A
Vertex
We name angles by the vertex or 3 letters. The middle letter is ALWAYS
the vertex.
Measurement of Angles
The unit of measure for angles is degrees. ° Ex. 90°
Right angle – has a measurement of 90°.
6
Acute angle – the measurement of the angle
is less than 90º.
Obtuse angle – has a measurement that is more
than 90º and less than 180º.
Angle Bisector – is a ray that bisects
( divides into 2 = parts)
the angle into 2 congruent (equal) angles.
Congruent angles have measures that are
equal.
Straight Angle – measures 180º
9/21/09
Reviewing Solving Equations
4X + 15 = 6X – 5
- 4X
-4X
1.) Move one variable by doing the opposite operation.
2.) Rewrite
15 = 2X -5
+5
+5
3.) Move the number so that the variable is alone.
4.) Rewrite
20 = 2X
5.) 2X is multiplication, divide to cancel out the 2.
2
2
10 = X
You solve equations by using opposite operations.
How to measure an angle with a protractor.
To Measure an Angle
 Step 1
Find the center hole on the straight edge of the protractor.
 Step 2
7
Place the hole over the vertex, or point, of the angle you wish to measure.
 Step 3
Line up the zero on the straight edge of the protractor with one of the sides of the angle.
 Step 4
Find the point where the second side of the angle intersects the curved edge of the
protractor.
 Step 5
Read the number that is written on the protractor at the point of intersection. This is the
measure of the angle in degrees.
8
9/22/09
Bisecting an Angle
Step 1. Draw a segment.
Step 2. Take a compass and its width greater than ½ of the segment.
Step 3. Put the point of the compass on one end of the segment and make an
arc above and below the segment. Repeat using the other endpoint.
Step 4. Connect the two intersections of the two sets of arcs with a
straight line.
9