Download Probability - NCSU Statistics

Unit 4 Probability Basics
• Laws of Probability
• Odds and Probability
• Probability Trees
Birthday Problem
• What is the smallest number of people you
need in a group so that the probability of 2
or more people having the same birthday is
greater than 1/2?
• Answer: 23
No. of people
23 30 40 60
Probability
.507 .706 .891 .994
Probability
•Formal study of uncertainty
•The engine that drives Statistics
• Primary objective of lecture unit 4:
1. use the rules of probability to calculate
appropriate measures of uncertainty.
2. Learn the probability basics so that we
can do Statistical Inference
Introduction
• Nothing in life is certain
• We gauge the chances of successful
outcomes in business, medicine, weather,
and other everyday situations such as the
lottery or the birthday problem
Tomorrow's Weather
Randomness and probability
Randomness ≠ chaos
A phenomenon is random if individual
outcomes are uncertain, but there is
nonetheless a regular distribution of
outcomes in a large number of repetitions.
Coin toss
The result of any single coin toss is
random. But the result over many tosses
is predictable, as long as the trials are
independent (i.e., the outcome of a new
coin flip is not influenced by the result of
the previous flip).
The probability of
heads is 0.5 =
the proportion of
times you get
heads in many
repeated trials.
First series of tosses
Second series
4.1 The Laws of Probability
Approaches to Probability
1. Relative frequency
event probability = x/n,
where x=# of occurrences of event of
interest, n=total # of observations
– Coin, die tossing; nuclear power plants?
• Limitations
repeated observations not practical
Approaches to Probability (cont.)
2. Subjective probability
individual assigns prob. based on personal
experience, anecdotal evidence, etc.
3. Classical approach
every possible outcome has equal
probability (more later)
Basic Definitions
• Experiment: act or process that leads to a
single outcome that cannot be predicted
with certainty
• Examples:
1. Toss a coin
2. Draw 1 card from a standard deck of cards
3. Arrival time of flight from Atlanta to RDU
Basic Definitions (cont.)
• Sample space: all possible outcomes of an
experiment. Denoted by S
• Event: any subset of the sample space S;
typically denoted A, B, C, etc.
Null event: the empty set F
Certain event: S
Examples
1. Toss a coin once
S = {H, T}; A = {H}, B = {T}
2. Toss a die once; count dots on upper face
S = {1, 2, 3, 4, 5, 6}
A=even # of dots on upper face={2, 4, 6}
B=3 or fewer dots on upper face={1, 2, 3}
3. Select 1 card from a
deck of 52 cards.
S = {all 52 cards}
Laws of Probability
1. 0  P ( A)  1, for any event A
2. P (F )  0, P ( S )  1
Probability rules (cont’d)
Coin Toss Example:
S = {Head, Tail}
Probability of heads = 0.5
Probability of tails = 0.5
3) The complement of any event A is the event
that A does not occur, written as A.
The complement rule states that the probability
of an event not occurring is 1 minus the
probability that is does occur.
P(not A) = P(A) = 1 − P(A)
Tail  = not Tail = Head
P(Tail ) = 1 − P(Tail) = 0.5

Venn diagram:
Sample space made up of an event
A and its complement A , i.e.,
everything that is not A.
Birthday Problem
• What is the smallest number of people you
need in a group so that the probability of 2
or more people having the same birthday is
greater than 1/2?
• Answer: 23
No. of people
23 30 40 60
Probability
.507 .706 .891 .994
Example: Birthday Problem
• A={at least 2 people in the group have a
common birthday}
• A’ = {no one has common birthday}
3 people
23 people
:P ( A') 
364
363

365
365
:
364
363
343
P ( A') 


 . 498
365
365
365
so P ( A )  1  P ( A ' )  1  . 498  . 502
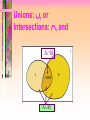
Unions: , or
Intersections: , and
A
A
Mutually Exclusive
(Disjoint) Events
Venn Diagrams
A and B disjoint: A  B=
• Mutually exclusive or
disjoint events-no outcomes
from S in common
A
A
A and B not disjoint
Addition Rule for Disjoint Events
4. If A and B are disjoint events, then
P(A or B) = P(A) + P(B)
Laws of Probability (cont.)
General Addition Rule
5. For any two events A and B
P(A or B) = P(A) + P(B) – P(A and B)
General Addition Rule
For any two events A and B
P(A or B) = P(A) + P(B) - P(A and B)
P(A) =6/13
+
A
P(B) =5/13
_
B
P(A and B) =3/13
P(A or B) = 8/13
A or B
20
Laws of Probability: Summary
•
•
•
•
1. 0  P(A)  1 for any event A
2. P() = 0, P(S) = 1
3. P(A’) = 1 – P(A)
4. If A and B are disjoint events, then
P(A or B) = P(A) + P(B)
• 5. For any two events A and B,
P(A or B) = P(A) + P(B) – P(A and B)
M&M candies
If you draw an M&M candy at random from a bag, the candy will have one
of six colors. The probability of drawing each color depends on the proportions
manufactured, as described here:
Color
Probability
Brown
Red
Yellow
Green
Orange
Blue
0.3
0.2
0.2
0.1
0.1
?
What is the probability that an M&M chosen at random is blue?
S = {brown, red, yellow, green, orange, blue}
P(S) = P(brown) + P(red) + P(yellow) + P(green) + P(orange) + P(blue) = 1
P(blue) = 1 – [P(brown) + P(red) + P(yellow) + P(green) + P(orange)]
= 1 – [0.3 + 0.2 + 0.2 + 0.1 + 0.1] = 0.1
What is the probability that a random M&M is any of red, yellow, or orange?
P(red or yellow or orange)
= P(red) + P(yellow) + P(orange)
= 0.2 + 0.2 + 0.1 = 0.5
Example: toss a fair die once
S = {1, 2, 3, 4, 5, 6}
• A = even # appears = {2, 4, 6}
• B = 3 or fewer = {1, 2, 3}
• P(A or B) = P(A) + P(B) - P(A and B)
=P({2, 4, 6}) + P({1, 2, 3}) - P({2})
= 3/6 + 3/6 - 1/6 = 5/6
End of First Part of Section 4.1