Download Study Guide and Intervention Angle Relationships

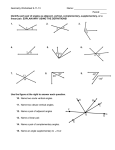
NAME ________________________________________ DATE ______________ PERIOD _____
10-1
Study Guide and Intervention
Angle Relationships
• An angle has two sides that share a common endpoint. The point where the sides meet is called the
vertex. Angles are measured in degrees, where 1 degree is one of 360 equal parts of a circle.
• Angles are classified according to their measure.
Right Angle
Acute Angle
Obtuse Angle
Straight Angle
• Two angles are vertical if they are opposite angles formed by the intersection of two lines.
• Two angles are adjacent if they share a common vertex, a common side, and do not overlap.
4
1
2
3
5
!1 and !3 are vertical angles.
!4 and !2 are vertical angles.
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
A.
C.
Classify each angle as acute, obtuse, right, or straight.
The angle is less
than 90°, so it is
an acute angle.
Example 2
1
2
!5 and !6 are adjacent angles
B.
The angle is greater
than 90°, so it is an
obtuse angle.
Label the two angles vertical or adjacent.
These angles are
vertical because they
are opposite each other
and formed by two
intersecting lines.
D.
3
4
These angles are
adjacent because they
share a common vertex,
a common side, and do
not overlap.
Exercises
Classify each angle as acute, obtuse, right, or straight.
1.
2.
3.
4.
7.
8.
Label the angles vertical or adjacent.
5.
6.
3
1 2
Chapter 10
6
4
5
151
7
8
Course 2
Lesson 10-1
Example 1
6
NAME ________________________________________ DATE ______________ PERIOD _____
10-2
Study Guide and Intervention
Complementary and Supplementary Angles
• Two angles are complementary if the sum of their measure is 90°.
m!1 ! m!2 " 90°
1
2
• Two angles are supplementary if the sum of their measure is 180°.
3
m!3 ! m!4 " 180°
4
• To find a missing angle measure, first determine if the angles are complementary or
supplementary. Then write an equation and subtract to find the missing measure.
Example 1
Find the value of x.
The two angles form a right angle or 90°, so they are complementary,
43 ! x " 90
Write the equation.
# 43
# 43
Subtract 43 from each side.
x " 47
43°
x°
Example 2
Find the value of x.
The two angles form a straight line or 180°, so they are supplementary,
110 ! x " 180
Write the equation.
# 110
# 110
Subtract 110 from each side.
x " 70
110˚
x˚
so the value of x is 70°.
Lesson 10-2
Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc.
so the value of x is 47°.
Exercises
Find the value of x in each figure.
2.
1.
58° x °
4.
3.
85°
56°
x°
5.
71°
Chapter 10
x°
6.
x°
x°
45°
82° x °
153
Course 2