Download Name: Date: Geometry Honors Unit 3 Quiz 1 Review Sections 3.5

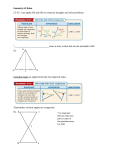
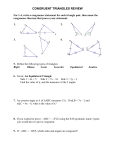
Name: __________________________________
Date: ____________________
Geometry Honors
Unit 3 Quiz 1 Review
Sections 3.5, 4.1-4.3, 4.6
1. Find the value of each variable.
x = _________°
y = _________°
z = _________°
2.
x = _________°
3. Use the diagram at the right to answer the questions.
a. Which angle is an exterior angle?
b. What are its remote interior angles?
c. Find m1 and m2.
m1 = _________°


m2 = _________°
WXYZ  JKLM. List each of the following.
4. Four pairs of congruent sides.
_________  _________
_________  _________

 _________
_________

 _________
_________
5.Four pairs of congruent angles.

 _________   _________

 _________   _________
 
 _________
  _________


 
 
 _________
  _________

 
ABCD  FGHJ. Find the measures of the given angles or lengths of the given sides.
A
D
F
J
B
C
G
H
6. mB = 3y, mG = y + 50
y = _________°
mB = _________°


mG = _________°
7. CD = 2x + 3; HJ = 3x + 2
x = _________
CD = _________

HJ = _________

Would you use SSS or SAS to prove the triangles congruent? If so, write a congruence statement. If there
is not enough information to prove the triangles congruent by SSS or SAS, write not enough information.
Explain your answer.
8.
9.
_________________________________
10.
_________________________________
_________________________________
11.
_________________________________
Name two triangles that are congruent by ASA.
12.
_________________________________
For each pair of triangles, tell why the two triangles are congruent. Give the congruence statement.
13.
14.
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
Proof Practice
Complete the following proofs.
15.
Given: WVZ and VWX are right angles.
WZ  VX
Prove: WVZ  VWX
Statements
Reasons
16.
̅̅̅̅ ; ̅̅̅̅
̅̅̅̅ ; ̅̅̅̅
̅̅̅̅
Given: ̅̅̅̅
𝐴𝐸 ∥ 𝐵𝐷
𝐸𝐵 ∥ 𝐷𝐶
𝐴𝐸 ≅ 𝐵𝐷
Prove: ∆𝐴𝐸𝐵 ≅ Δ𝐵𝐷𝐶
Statements
Reasons
17. Given: B and D are right angles.
AE bisects BD
Prove: ABC  EDC
Statements
Reasons
18. Given: BC  DC, AC  EC
Prove: ABC  EDC
Statements
19.
20.
21.
22.
23.
24.
NOTE: Review Proof Packets as well
Reasons