Download 3.3 Prove Lines are Parallel

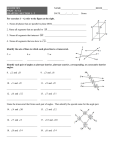
Mathematician: _________________________ Date: _______________ Core-­‐Geometry: 3.3 Prove lines are parallel Warm-­‐up: 1. Write the equation so that y is a function of x: 4y − x = 20 − y 2. 117 is 78% of what number? 10
k
=
3. Solve the proportion: 17 2k − 3 Ch 1 Review 1. The expressions (3x + 63)° and (7x – 45)° represent the measures of two angles of a
regular decagon. Find the measure of an angle of the decagon.
2. Draw a linear pair of angles, then define linear pair.
1 3.3 Proving Lines are Parallel In Unit 1 you learned to write conditional statements and their converses. Sometimes the converse can also be used to prove relationships. ______________________________ lines and transversals create special angle pair relationships. Some of the angle pairs were ________________________ and some of the pairs were ______________________________. Congruent angle pairs Supplementary angle pairs Identify the angle pairs below. a) b) d) c) If we can identify the special angles above and show that they are congruent or supplementary (just _______________________________ interior angles), then we know that the two lines cut by the transversal are ____________________________. 2 Example 1 Use Angle Relationships and Algebra First identify the angle pair, then find the value of x that makes 𝑚||𝑛. a) b) c) e) f) d) Example 2 Parallel or Not? Can we tell that the lines below are parallel or not? If yes, identify the angle pair and the relationship of the pair. If no, then explain why. a) c) b) d) 3 Example 3: More Challenging Angle Measures Identify angle pairs to find the missing angle measures created by parallel lines and the transversal below. You may need to use what you know from Unit 1 about straight angles, linear pairs, and vertical angles. 1. a = b= c= a = b= c= d= 2. 4 3. a= b= c= d= e= f= Hmwk 2.3 p. 165, #1, 3, 5, 6, 8, 10,11,13,14 and p. 160 Quiz at bottom of page 5