Download Physics 1304: Lecture 4 Notes

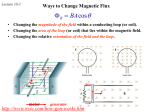
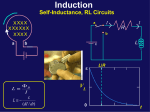
Self Inductance and RL Circuits
B(t)
i
R
~
a
I
I
b
e
L
Physics 1304: Lecture 15, Pg 1
Lecture Outline
l
Concept of Self-Inductance
l
Definition of Self-Inductance
l
Calculation of Self-Inductance for Simple Cases
l
RL Circuits
l
Energy in Magnetic Field
Text Reference: Chapter 32
Physics 1304: Lecture 15, Pg 2
Self-Inductance
Consider the loop at the right.
l
•
X XX X
X XX XX X
X XX X
switch closed Þ current starts to flow
in the loop.
• \ magnetic field produced in the area
enclosed by the loop.
• \ flux through loop changes
•
•
\ emf induced in loop opposing initial emf
Self-Induction: the act of a changing current through a loop
inducing an opposing current in that same loop. Just as a
variable current can induce an EMF on another coil, it can
induce an EMF on itself (back EMF).
Physics 1304: Lecture 15, Pg 3
Self-Inductance
l
We can put solenoids in a circuit:
R
a
I
Because of the back EMF the current in
this circuit does not instantaneously
reach steady state. This is due to the
presence of the solenoid L.
b
L
e
Recall that
for a solenoid
}
Flux
through
one loop
B  0 ni
Flux through the whole solenoid is
Thus,
N 
0 N 2 A
l
Faradays Law
then takes form,
i
or,
}
  BA
  0 n Ai
N
N  Li
where,
L
0 N 2 A
l

Physics 1304: Lecture 15, Pg 4
Self-Inductance
The inductance of an inductor ( a set of coils in some geometry ..eg
solenoid, toroid) then, like a capacitor, can be calculated from its
geometry alone if the device is constructed from conductors and
air.
l
If extra material (eg iron core) is added, then we need to add some
knowledge of materials as we did for capacitors (dielectrics) and
resistors (resistivity)
l
•
Archetypal inductor is a long solenoid, just as a pair of parallel
plates is the archetypal capacitor.
l
r
N turns
r << l
A
++++
d -----
d  A
Physics 1304: Lecture 15, Pg 5
Self-Inductance
Units of Inductance are Henrys:
[H ]
Vs
[ H ] :[ ]
A
Physics 1304: Lecture 15, Pg 6
Lecture 19, CQ
l
Consider the two inductors shown:
ç Inductor 1 has length l, N total turns and
has inductance L1.
ç Inductor 2 has length 2l, 2N total turns
and has inductance L2.
ç What is the relation between L1 and L2?
(a) L2 < L1
(b) L2 = L1
l
2l
r
r
N turns
r
2N turns
(c) L2 > L1
Physics 1304: Lecture 15, Pg 7
Lecture 19, CQ
l
Consider the two inductors shown:
ç Inductor 1 has length l, N total turns and
has inductance L1.
ç Inductor 2 has length 2l, 2N total turns
and has inductance L2.
ç What is the relation between L1 and L2?
(a) L2 < L1
(b) L2 = L1
l
2l
r
r
N turns
r
2N turns
(c) L2 > L1
• To determine the self-inductance L, we need to determine the flux B
which passes through the coils when a current I flows: L  B / I.
• To calculate the flux, we first need to calculate the magnetic field B
produced by the current: B = 0(N/l)I
• ie the B field is proportional to the number of turns per unit length.
• Therefore, B1 = B2. But does that mean L1 = L2?
• To calculate L, we need to calculate the flux.
• Since B1 = B2 , the flux through any given turn is the same in each
inductor.
• However, there are twice as many turns in inductor 2; therefore the
flux through inductor 2 is twice as much as the flux through inductor
1!!! Therefore, L2 = 2L1.
Physics 1304: Lecture 15, Pg 8
Physics 1304: Lecture 15, Pg 9
RL Circuits
•
At t=0, the switch is closed and
the current I starts to flow.
a
I
I
R
b
•
Loop rule:
e
L
Note that this eqn is identical in form to that for the RC circuit with the following
substitutions:
 RCRL:
RC:
\

Physics 1304: Lecture 15, Pg 10
Lecture 18, ACT 2
1) At t=0 the switch is thrown from position
b to position a in the circuit shown:
ç What is the value of the current I a long
time after the switch is thrown?
a
I
I
R
b
e
L
R
(a) I = 0
(b) I = e / 2R
(c) I = 2e / R
• A long time after the switch is thrown, the current approaches an
asymptotic value. ie as t , dI/dt 0.
• As dI/dt 0 , the voltage across the inductor 0. \ I = e / 2R.
2) What is the value of the current I0 immediately after
the switch is thrown?
(a) I0 = 0
(b) I0 = e / 2R
(c) I0 = 2e / R
• Immediately after the switch is thrown, the rate of change of current
is as large as it can be (we’ve been assuming it was !)
• The inductor limits dI/dt to be initially equal to e/ L. ie the voltage
across the inductor = e; the current then must be 0!
Physics 1304: Lecture 15, Pg 11
RL Circuits
l
To find the current I as a fcn of
time t, we need to choose an
exponential solution which
satisfies the boundary
condition:
a
I
I
b
L

•
We therefore write:
•
The voltage drop across the inductor is given by:
Physics 1304: Lecture 15, Pg 12
RL Circuit (e on)
1
e/R
Max = e/R
Q
Current
L/R
2L/R
1
2
Sketch curves !
f( x ) 0.5
I
63% Max at t=L/R
00
Voltage on L
Max = e/R
1 e1
0
t
3
4
t
3
4
x
t/RC
f( x )V
0.5
L
37% Max at t=L/R
0.0183156
0
0
1
2
Physics 1304: Lecture 15, Pg 13
RL Circuits
l
•
After the switch has been in
position a for a long time,
redefined to be t=0, it is moved to
position b.
a
I
I
R
b
Loop rule:
e
•
The appropriate initial condition is:
•
The solution then must
have the form:
L

Physics 1304: Lecture 15, Pg 14
RL Circuit (e off)
e/R
1 1
Current
L/R
2L/R
1
2
Sketch curves !
f( x ) 0.5
I
Max = e/R
37% Max at t=L/R
0.0183156
0
0
10 0
Max = -e
37% Max at t=L/R
Q
Voltage on L
t
3
x
4
4
f( x ) 0.5
V
L
-e
0
0
1
2
t
3
4
Physics 1304: Lecture 15, Pg 15
e on
L/R
1
e/R
2L/R
I
I
f( x ) 0.5
1

1 e1

4
0
0
1
01 0
dI
 ee  Rt / L
dt
Q
VL  L
0
1
2
t
3
4
2
t
3
x
4
4
f( x )V0.5
L
VL  L
0
e  Rt / L
e
R
f( x ) 0.5
I
0.0183156
3
2L/R
I
x
t/RC
f( xV
) 0.5
L
83156
t
2
L/R
e/R
1 1
e
1  e  Rt / L
R
00
0
e off
-e0
0
dI
  ee  Rt / L
dt
t 3
1 Physics2 1304:
Lecture 15,4Pg 16
Lecture 18, ACT 3
l
At t=0, the switch is thrown from position b to
position a as shown:
ç Let tI be the time for circuit I to reach 1/2 of
its asymptotic current.
ç Let tII be the time for circuit II to reach 1/2
of its asymptotic current.
ç What is the relation between tI and tII?
(a) tII < tI
(b) tII = tI
(c) tII > tI
• To answer this question, we must determine
the time constants of the two circuits.
• To determine the time constants of the two
circuits, we just need to write down the loop
eqns:
I:
II:
I
a
I
R
b
I
e
L
R
a
I
I
b
e
L
II
R
L
Can you determine from
this the rule for adding
inductors in series?
Physics 1304: Lecture 15, Pg 17
Energy of an Inductor
l
How much energy is stored in an
inductor when a current is flowing
through it?
I
a
I
R
b
•
e
Start with loop rule:
L
• Multiply this equation by I:
•
From this equation, we can identify PL, the rate at which energy is
being stored in the inductor:
•
We can integrate this equation to find an expression for U, the
energy stored in the inductor when the current = I:

Physics 1304: Lecture 15, Pg 18
Where is the Energy Stored?
l
Claim: (without proof) energy is stored in the Magnetic field itself (just as in the
Capacitor / Electric field case).
l
To calculate this energy density, consider the uniform field generated by a long
solenoid:
l
•
The inductance L is:
r
N turns
•
Energy U:
•
We can turn this into an energy density by dividing by the
volume containing the field:
Physics 1304: Lecture 15, Pg 19
Physics 1304: Lecture 15, Pg 20