Download Histogram statistics for image enhancement Let r denote a discrete

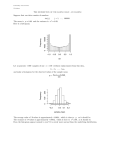
Histogram statistics for image enhancement
Let r denote a discrete random variable representing intensity representing intensity values in [0, L-1] and let p(ri)denote the normalised histogram component corresponding to value r .We may view p(ri ) as an estimate of the probability that infinity ri occurs in the image
µn=
( −
) p( )
nth moment about its mean
m is the mean(average intensity)
m =∑
r p( )
µl =
( −
) p( ) =
Global mean and variance a computed on an entire image and a useful for gross
adjustment in overall intensity and contrast.
A more powerful use of these parameters is in local enhancement, where local
mean and variance are used as the basis for making changes.
S xy denote a neighbourhood of a specified useful(x, y). The mean value of the
pixel is given by
=∑
( )
=
(r − m
)
( )
Enhance the dark area while leaving the light area unchanged as possible.
Fundamentals of spatial filtering:Filtering is useful for amplifying (passing) or rejecting certain frequency components.
w(-1, 1)
w(0, -1)
w(1,- 1)
w(-1, 0)
w(0,0)
w(1, 0)
w(-1, 1)
w(0,1)
w(1,1)
Filter that passes low frequency is called low pass. The net effect produced by a
low pass filter is to blur (smooth) the image. we can accomplish a similar
smoothing directly on the image itself by using spatial filter .There is a linear
one –to-one correspondence between linear spatial filters and filters in the frequency domain.
spatial filtering is more versatile than the filtering in the frequency domain as
spatial filtering can be used for non-linear filtering.
The mechanics of spatial filtering:Spatial filter consists of (1) a neighbourhood, (2) a predefined operation that is
performed on the image pixels encompassed by the neighbourhood.
Linear and non-linear filtersAt any point (x, y) is the image, the response g(x, y) of the filter is the sum of
products of the filter coefficient and the pixels encompassed by filters.
For a mask of m x n, we assume that
m= 2n+1 and n=2b+1 where a, b a position integers.
In general, linear spatial filtering of an image of size M x N with filter size m x
n is given by
g (x, y)=∑
∑
( , ). ( + , + ).
Spatial correlation and convolution:There are two clearly related concepts in linear filtering. One is correlation and
other is convolution. Correlation is the process of moving the filter mask on the
image and computing the sum of products of at each location. The mechanism
of convolution is the sum, except that the filter is first related by 180
(a)
(b)
0 0 0 1 0 0 0 0 w= 1 2 3 2 8
0000000100000000
12328
→00082321000
Full correlation
 Correlation is a function of displacement of the filter
 Correlating a filter w with a function that contains a single 1with the rest
being 0’s result that is a copy of w rotated by 180ᵒ
 If the filter mask is symmetric correlation and convolution yield the same
result
 Correlation can be used to find matches between images
W(x,y).f(x,y)=∑
∑
( , ). ( + , + )
a= (m-1)/2, n= (n-1)/2 are odd integers,
W(x, y)* f(x, y) → convolution
( , ) ( − , − )
Exercise
(1) In some applications it is useful to model the histogram of input images
as Gaussian probability density function as –
pr (r) =
√
.
(
)
Ϭ
What is the transformation function you would use for histogram normalization?
Hint:
S=T (Ϭ) = (L-1)∫
= (L-1)∫
(w)dw
(
√
Ϭ
)
Ϭ
dw
Exercise
(2) Suppose that a digital image is subjected to histogram equalization. Show
that a second pass of histogram equalization (on the histogram equalized
image) will produce exactly the same result as the first pass.