* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Summer School 2003, Bertinoro - LAR-DEIS
Survey
Document related concepts
Transcript
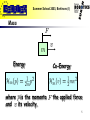
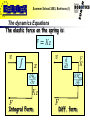
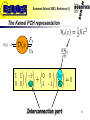
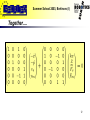
Summer School 2003, Bertinoro (I) Dirac Framework for Robotics Tuesday, July 8th, (4 hours) Stefano Stramigioli © Stefano Stramigioli Summer School 2003, Bertinoro (I) Contents • 1D Mechanics: as introduction • 3D Mechanics – Points, vectors, line vectors screws – Rotations and Homogeneous matrices – Screw Ports – Rigid Body Kinematics and Dynamics – Springs – Interconnection and Mechanisms Dynamics 2 Summer School 2003, Bertinoro (I) 1D Mechanics © Stefano Stramigioli Summer School 2003, Bertinoro (I) 1D Mechanics • In 1D Mechanics there is no geometry for the ports: efforts/Forces and flows/velocities are scalar • Starting point to introduce the basic elements for 3D 4 Summer School 2003, Bertinoro (I) Mass Energy where is the momenta and its velocity. Co-Energy the applied force 5 Summer School 2003, Bertinoro (I) The dynamics Equations The second Law of dynamics is: Integral Form Diff. form 6 Summer School 2003, Bertinoro (I) The Kernel PCH representation Interconnection port 7 Summer School 2003, Bertinoro (I) Spring Energy Co-Energy where is the displacement the applied force to the spring and its relative velocity. 8 Summer School 2003, Bertinoro (I) The dynamics Equations The elastic force on the spring is: Integral Form Diff. form 9 Summer School 2003, Bertinoro (I) The Kernel PCH representation Interconnection port 10 Summer School 2003, Bertinoro (I) Mass-Spring System • Spring • Mass 11 Summer School 2003, Bertinoro (I) Together…. 12 Summer School 2003, Bertinoro (I) Interconnection of the two subsystems (1 junc.) Or in image representation 13 Summer School 2003, Bertinoro (I) Combining… There exists a left orthogonal 14 Summer School 2003, Bertinoro (I) Finally 15 Summer School 2003, Bertinoro (I) Summary and Conclusions • All possible 1D networks of elements can be expressed in this form • Dissipation can be easily included terminating a port on a dissipating element • Interconnection of elements still give the same form 16 Summer School 2003, Bertinoro (I) 3D Mechanics © Stefano Stramigioli Summer School 2003, Bertinoro (I) Notation Set of points in Euclidean Space Free Vectors in Euclidean Space Right handed coordinate frame I Coordinate mapping associated to 18 Summer School 2003, Bertinoro (I) Rotations 19 Summer School 2003, Bertinoro (I) Rotations It can be seen that if purely rotated and are where 20 Summer School 2003, Bertinoro (I) Theorem If of time is a differentiable function are skew-symmetric and belong to : 21 Summer School 2003, Bertinoro (I) Tilde operator 22 Summer School 2003, Bertinoro (I) is a Lie algebra • The linear combination of skew-symmetric matrices is still skew-symmetric • To each matrix we can associate a vector such that … It is a vector space • It is a Lie Algebra !! 23 Summer School 2003, Bertinoro (I) SO(3) is a Group It is a Group because • Associativity •Identity •Inverse 24 Summer School 2003, Bertinoro (I) It is a Lie Group (group AND manifold) • • where • where • Lie Algebra Commutator 25 Summer School 2003, Bertinoro (I) Lie Groups Common Space thanks to Lie group structure 26 Summer School 2003, Bertinoro (I) Dual Space • For any finite dimensional vector space we can define the space of linear operators from that space to co-vector The space of linear operators from to (dual space of ) is indicated with 27 Summer School 2003, Bertinoro (I) In our case we have Configuration Independent Port ! 28 Summer School 2003, Bertinoro (I) General Motion 29 Summer School 2003, Bertinoro (I) General Motions It can be seen that in general, for right handed frames where , 30 Summer School 2003, Bertinoro (I) Homogeneous Matrices • Due to the group structure of it is easy to compose changes of coordinates in rotations • Can we do the same for general motions ? 31 Summer School 2003, Bertinoro (I) SE(3) 32 Summer School 2003, Bertinoro (I) Theorem If of time belong to is a differentiable function where 33 Summer School 2003, Bertinoro (I) Tilde operator 34 Summer School 2003, Bertinoro (I) Elements of se(3): Twists The following are vector and matrix coordinate notations for twists: The following are often called twists too, but they are no geometrical entities ! 9 change of coordinates ! 35 Summer School 2003, Bertinoro (I) SE(3) is a Group It is a Group because • Associativity •Identity •Inverse 36 Summer School 2003, Bertinoro (I) SE(3) is a Lie Group (group AND manifold) • • where • where • Lie Algebra Commutator 37 Summer School 2003, Bertinoro (I) Lie Groups Common Space thanks to Lie group structure 38 Summer School 2003, Bertinoro (I) Intuition of Twists Consider a point fixed in : and consider a second reference where and 39 Summer School 2003, Bertinoro (I) Possible Choices For the twist of we consider possibilities with respect to and we have 2 40 Summer School 2003, Bertinoro (I) Left and Right Translations 41 Summer School 2003, Bertinoro (I) Possible Choices and 42 Summer School 2003, Bertinoro (I) Notation used for Twists For the motion of body with respect to body expressed in the reference frame we use or The twist is an across variable ! Point mass geometric free-vector Rigid body geometric screw + Magnitude 43 Summer School 2003, Bertinoro (I) Chasle's Theorem and intuition of a Twist Any twist can be written as: 44 Summer School 2003, Bertinoro (I) Examples of Twists 45 Summer School 2003, Bertinoro (I) Examples of Twists 46 Summer School 2003, Bertinoro (I) Changes of Coordinates for Twists • It can be proven that 47 Summer School 2003, Bertinoro (I) Wrenches • Twists belong geometrically to • Wrenches are DUAL of twist: • Wrenches are co-vectors and NOT vectors: linear operators from Twists to Power • Using coordinates: 48 Summer School 2003, Bertinoro (I) Poinsot's Theorem and intuition of a Wrench Any wrench can be written as: 49 Summer School 2003, Bertinoro (I) Chasles vs. Poinsot Charles Theorem Poinsot Theorem The inversion of the upper and lower part corresponds to the use of the Klijn form 50 Summer School 2003, Bertinoro (I) Vectors, Screws as “Forces” • Forces and Wrenches are co-vectors, but: – Euclidean metric vector interpretation of a Force – Klein’s form screw interpretation of a Wrench That is identification of dual spaces. 51 Summer School 2003, Bertinoro (I) Example of the use of a Wrench Finding the contact centroid Contact Point (Center of Pressure) Measured Wrench 6D sensor 52 Summer School 2003, Bertinoro (I) Transformation of Wrenches • How do wrenches transform changing coordinate systems? We have seen that for twists: 53 Summer School 2003, Bertinoro (I) Changes of coordinates MTF 54 Summer School 2003, Bertinoro (I) In Dirac Kernel form MTF 55 Summer School 2003, Bertinoro (I) Power Port A B belong to vector spaces in duality: such that there exists a bilinear operator 56 Summer School 2003, Bertinoro (I) Finite dimensional case • If is finite dimensional defined, namely is uniquely where indicates the uniquely defined set of linear operators from to Elements of are vectors Elements of are co-vectors 57 Summer School 2003, Bertinoro (I) In Robotics Is the v.s. of Twists Is the v.s. of Wrenches 58 Summer School 2003, Bertinoro (I) Power and Inf. Dim Case A B • represents the instantaneous power flowing from A to B • For inf.dim. systems they belong to k and (n-k) (Lie-algebra-valued) forms 59 Summer School 2003, Bertinoro (I) Dynamics © Stefano Stramigioli Summer School 2003, Bertinoro (I) Contents • time derivative • • • • Rigid Body dynamics Spatial Springs Kinematic Pairs Mechanism Topology 61 Summer School 2003, Bertinoro (I) time derivative • is function of time • It can be proven that where 62 Summer School 2003, Bertinoro (I) Transformations of If we have like? ,how does look 63 Summer School 2003, Bertinoro (I) It can be shown that in general 64 Summer School 2003, Bertinoro (I) Rigid Bodies Dynamics © Stefano Stramigioli Summer School 2003, Bertinoro (I) Rigid bodies A rigid Body is characterised by a (0,2) tensor called Inertia Tensor: and we can then define the momentum screw: where the Kinetic energy is 66 Summer School 2003, Bertinoro (I) Generalization of Newton’s law In an inertial frame, for a point mass we had This can be generalized for rigid bodies Where Ni0 is the moment of body expressed in the inertial frame 0 . That is why momenta is a co-vector !! 67 Summer School 2003, Bertinoro (I) And in body coordinates ? Using the derivative of AdH 68 Summer School 2003, Bertinoro (I) ….. multiplying on the left for we get 69 Summer School 2003, Bertinoro (I) and since we have that and we eventually obtain 70 Summer School 2003, Bertinoro (I) Momentum dynamics which is called Lie-Poisson reduction. NOTE: No information on configuration ! 71 Summer School 2003, Bertinoro (I) Other form Defining which is linear and anti-symmetric 72 Summer School 2003, Bertinoro (I) Port-Hamiltonian form 73 Summer School 2003, Bertinoro (I) Port-Hamiltonian form Modulation Storage port Interconnection port 74 Summer School 2003, Bertinoro (I) Geometric Springs © Stefano Stramigioli Summer School 2003, Bertinoro (I) Spatial Springs If, by means of control, we define a 3D spring using a parameterization like Euler angles, we do not have a geometric description of the spring: no information about the center of compliance, instead: Morse Theory 4 cells: 1 stable+3 unstable points 76 Summer School 2003, Bertinoro (I) Spatial Springs where where 77 Summer School 2003, Bertinoro (I) For Constant Spatial Spring It could be shown that: Storage port to integrate! Interconnection port 78 Summer School 2003, Bertinoro (I) Parametric Changes (Scalar Case) 79 Summer School 2003, Bertinoro (I) Variable Spatial Springs (Geometric Case) Length Variation Body 1 Variation RCC Body 2 It can be shown that varying RCC does NOT exchange energy !! 80 Summer School 2003, Bertinoro (I) Kinematic Pairs © Stefano Stramigioli Summer School 2003, Bertinoro (I) Kinematic Pair • A n-dof K.P. is an ideal constraint between 2 rigid bodies which allows n independent motions • For each relative configuration of the bodies we can define Allowed subspace of dimension n Actuation subspace of dimension n 82 Summer School 2003, Bertinoro (I) Decomposition of and ! n n 6-n 6-n 83 Summer School 2003, Bertinoro (I) Representations of subspaces To satisfy power continuity 84 Summer School 2003, Bertinoro (I) And in the Kernel Dirac representation Interconnection port Actuators ports 85 Summer School 2003, Bertinoro (I) Mechanism Topology © Stefano Stramigioli Summer School 2003, Bertinoro (I) Network Topology • Interconnection of q rigid bodies by n nodic elements (kinematic pairs, springs or dampers). • We can define the Primary Graph describing the mechanism and than: Port connection graph= Lagrangian tree + Primary Graph 87 Summer School 2003, Bertinoro (I) Primary Graph 88 Summer School 2003, Bertinoro (I) Primary Graph • The Primary graph is characterised by the Incedence Matrix 89 Summer School 2003, Bertinoro (I) Lagrangian Tree 90 Summer School 2003, Bertinoro (I) Fundamental Loop Matrix Lagrangian Tree Primary Graph 91 Summer School 2003, Bertinoro (I) Fundamental Cut-set Matrix Lagrangian Tree Primary Graph 92 Summer School 2003, Bertinoro (I) `Power Continuity Power continuity ! 93 Summer School 2003, Bertinoro (I) Mechanism Dirac Structure Power Ports Rigid Bodies Power Ports Nodic Elements 94 Summer School 2003, Bertinoro (I) Further Steps… 95 Summer School 2003, Bertinoro (I) • • • • • • Conclusions Any 3D part can be modeled in the Dirac framework Any interconnection also ! In this case the ports have a geometrical structures: no scalars ! Some steps still to go to bring the system in explicit form A lot of extensions are possible Not trivial to bring everything in simplified explicit form 96