Download Chapter 5

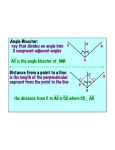
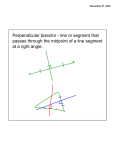
Journal
Chapter
5
•Perpendicular Bisector and
Theorem
•Angle Bisector and Theorem
•Concurrency
•Concurrency of
Perpendicular Bisectors
•Circumcenter
•Concurrency of Angle
Bisectors
•Incenter
•Median
•Centroid
•Concurrency of Medians
•Altitude of a Triangle
•Orthocenter
•Concurrency of Altitudes
•Midsegment and Theorem
•Longer and Shorter Sides
•Angle and Triangle inequality
•Indirect Proofs
•Hinge Theorem
•Triangle Relationships
Kirsten Erichsen
9-5
What is a Perpendicular Bisector?
A perpendicular
bisector is a line
that bisects a
segment and is
perpendicular to
the line being
bisected.
The perpendicular
bisector passes right
through the middle of the
line or segment.
Example 1.
The Perpendicular
Bisector, bisects
the segment or
line right through
the middle.
The perpendicular bisector bisects right through the middle of the segment.
Example 2.
The Perpendicular
Bisector passes
through the line to
make up four 90°
angles.
The perpendicular bisector bisects right through the middle of the segment.
Example 3.
Remember, the
perpendicular
bisector bisects
through the middle,
so both sides of the
line after they have
been bisected are
congruent.
The perpendicular bisector bisects right through the middle of the segment.
Perpendicular Bisector Theorem.
• If a point is on the perpendicular
bisector, then it is equidistant to
both endpoints of the segment.
• CONVERSE: If a point is
equidistant to both endpoints,
then it lies on the perpendicular
bisector.
Example 1.
Since point P lies
on the
Perpendicular
Bisector, then it is
has the same
measure to both
sides. So in
conclusion, the
measurement
from P to J is 6
centimeters.
The measurements from point P to point J are also 6 cm.
Example 2.
Since point P lies
on the
Perpendicular
Bisector, then it is
has the same
measure to both
sides. So in
conclusion, the
measurement
from G to C is 9
centimeters.
The measurement from point G to point C is 9 cm.
Example 3.
Since point P lies
on the
Perpendicular
Bisector, then it is
has the same
measure to both
sides. So in
conclusion, the
measurement
from J to L is 15
centimeters.
The measurement from point J to point L is 15 cm.
What is an Angle Bisector?
An Angle
Bisector is a ray
or line that cuts
an angle into 2
congruent
angles.
The angle bisector that
cuts the angle, always has
to be in the interior or
inside of the angle.
Example 1.
The right
angle is
bisected
into 2
congruent
angles, both
measuring
45°.
The ray (purple) is the angle bisector.
Example 2.
The obtuse
angle
measures
140°. Since it
has been
bisected,
both angles
measure 70°.
The ray (green) is the angle bisector.
Example 3.
The acute
angle measures
45°. Since it has
been bisected
by a ray, then
each one of
the angles
measures 22.5°.
The ray (green) bisects the acute angle.
Angle Bisector Theorem.
• Any point that lies on the angle
bisector, is equidistant to both
sides of the angle.
• CONVERSE: If it is equidistant to
both sides of the angle, then it
lies on the angle bisector.
Example 1.
To find the length
of the other
length, then follow
the Angle Bisector
Theorem. If it lies
on the bisector
then it is
congruent to both
sides.
The length from point D to point E is 15 centimeters.
Example 2.
Both sides are
congruent if the
point lies in the
Angle Bisector.
The length from J
to K is congruent
to the length of J
to N.
The length from point J to N is 9 centimeters.
Example 3.
Both sides are
congruent if the
point lies in the
Angle Bisector.
The length from W
to V is congruent
to the length of W
to X.
The length from point W to point X is 35 centimeters.
What is Concurrency?
Concurrent: it is
said when three or
more lines intersect
at one point.
The point of
intersection is
called the point of
concurrency.
Example 1.
A
All 3 lines are
concurrent
because they
intersect at
the same
point of
concurrency.
The point of Concurrency is point A.
Example 2.
J
All 4 lines are
concurrent
because they
intersect at
the same
point of
concurrency.
The point of Concurrency is point J.
Example 3.
L
All 4 lines are
concurrent
because they
intersect at
the same
point of
concurrency.
The point of Concurrency is point L.
Concurrency of Perpendicular
Bisectors.
• The perpendicular
bisectors of a
triangle intersect
at a point that is
equidistant from
the vertices of a
triangle.
• This is also called
the circumcenter.
Example 1.
Example 2.
Example 3.
It is 6 cm to the endpoints, because it lies on the Perpendicular Bisector
What is the Circumcenter?
• The circumcenter is the point of
concurrency of the three bisectors
of a triangle.
• The circumcenter of a triangle is
equidistant from the vertices of
the triangle.
Example 1.
In a right triangle the
circumcenter is always
meet and are going to
be on the lines or
segments of the
triangle.
The Perpendicular Bisectors starts from the Midpoint and make a straight line.
Example 2.
In an obtuse triangle
the circumcenter is
always outside of the
triangle no matter
what.
The lines always start from the midpoint and make a straight line.
Example 3.
In an acute triangle
the circumcenter is
always in the inside of
the triangle no matter
what.
You always start from the midpoint of each side and make a straight line (PB).
Concurrency of Angle Bisectors.
• The angle bisectors are also
concurrent to each other.
• Since a triangle has three angles,
it has three angle bisectors that
are concurrent.
• It can also be referred as the
incenter.
Example 1.
All of the lines in blue are concurrent because they intersect at the same
place. The lines in red are congruent because they have the same lengths.
Example 2.
The lines in red are the same lengths from the point of concurrency to the
sides of the triangle.
Example 3.
The lines in red are the same lengths from the point of concurrency to the
sides of the triangle.
What is the Incenter?
• INCENTER: it is the point of
concurrency of the three angle
bisectors of a triangle.
• The incenter of a triangle is
equidistant from the sides of the
triangle.
• It is always going to be inside the
triangle.
Example 1.
The
incenter in
an acute
triangle is
always
going to
be inside.
Example 2.
The
incenter in
a right
triangle is
always
going to
be inside.
Example 3.
The incenter in an obtuse triangle is always going to be inside.
What is the Median?
• MEDIAN: a segment
whose end points are
a vertex of a triangle
and a midpoint.
• The midpoint has to
be from the opposite
side of the triangle.
C
D
Example 1.
I
J
K
H
The Median of this triangle is from point K to point J, but there can be 2 more.
Example 2.
L
N
M
The median being shown is from point L to point M.
O
Example 3.
B
D
A
C
The Median being shown is from point D to point C.
What is the Centroid?
• CENTROID: the point of concurrency of
the three medians of a triangle.
• The centroid is always in the inside of
the triangle.
• The centroid of a triangle is located ⅔
of the distance from each vertex to
the midpoint of the opposite side.
Example 1.
To find the centroid, bisect the angle.
Example 2.
Connect
the
angle
bisector
to the
midpoint
of the
opposite
side.
Example 3.
The point of intersection is the centroid of the triangle.
Concurrency of the Medians.
All of the
Medians in a
triangle are
concurrent to
each other.
Altitude of Triangles.
• Altitude of Triangles: a perpendicular
segment from a vertex to the line
containing the opposite side.
• Every single triangle has three
altitudes.
• It can be inside, outside or on the
triangle.
Example 1.
In this triangle the altitude is 4.5 centimeters.
Example 2.
In this triangle the altitude is 3 centimeters.
Example 3.
In this triangle the altitude is 11 centimeters.
What is the Orthocenter?
• ORTHOCENTER: the point of
concurrency of the three
altitudes of a triangle.
• The concurrent altitudes either
intersect inside (acute), outside
(obtuse) or on the vertex of the
right angle.
Example 1.
Example 2.
Example 3.
What is a Midsegment?
• MIDSEGMENT: a segment that joins two
midpoints of the sides of the triangles
• The midsegment is parallel to the
opposite side.
• The Midsegment is half as long as the
opposite side.
• THEOREM: a midsegment is parallel to
a side of the triangle and it is half the
length of that side.
Example 1.
The Midsegment shown here is from point D to point E.
Example 3.
It is 6 cm to the endpoints, because it lies on the Perpendicular Bisector
Example 3.
It is 6 cm to the endpoints, because it lies on the Perpendicular Bisector
Relationship between Longer and
Shorter Sides and the Opposite Angles
• If two sides of a triangle are not
congruent, then the larger angle is
opposite the longer side.
• If two angles of a triangle are not
congruent, then the longer side side is
opposite the larger angle.
• The smallest side is opposite to the
shortest angle.
• The medium side is opposite to the
medium angle
Example 1.
M<S > M<A
The larger angle is opposite to
the longer isde.
S
A
Example 2.
M<A > M<C
Angle A is
opposite from
the largest side.
Example 3.
Angle A is opposite
from the shortest side.
U
Exterior Angle Inequality.
• An exterior angle of a
triangle is greater than
either of the non-adjacent
interior angles.
Example 1.
Example 2.
Example 3.
Triangle Inequality.
• The sum of any two side lengths of
a triangle is great than the third
side length
• The two sides are the two shortest
lengths of the triangle.
• The third side is the longest side or
hypotenuse.
Example 1.
It is a triangle because the sums of the legs are greater than the longest side.
Example 2.
It is a triangle because the sum of the sides are greater than the longest
side.
Example 3.
It is not a full triangle because the sum of the shortest sides equal the longest
side.
Indirect Proofs.
• In this type of proof you use logical
argument.
STEPS TO FOLLOW:
• Identify the conjecture that needs to be
proven.
• Assume the opposite of the conclusion
• Use direct reasoning to show that is leads to
a contradiction.
• Conclude that the assumption is false, so the
original statement/conjecture must be true.
Example 1.
A
B
C
D
Statement:
1. AD is perp to BC
2. BDA is a straight
angle
3. M<BDA = 180°
4. <BDA is a right
angle
5. M<BDA = 90°
6. <BDA is not a
straight angle
Reason:
1. Given
2. Assume that is
it false
3. Def. of St. Ang
4. Def. of Perp.
Lines
5. Def. of Rt. Ang
6. Contradiction
Example 2.
L
K
Reason:
Statement:
1. Given
1. Δ JKL is a right Δ
2. ΔJKL is obstuse (<K) 2. Assume
3. Acute <‘s of rt Δ
3. M<K + m<L = 90°
are comp.
4. M<K = 90° - m<L
4. Subtract Prop
5. M<K > 90°
5. Def. of obtuse
6. 90° - m<L >90°
6. Substitution
7. M<L <0°
8. ΔJKL doesn’t have an7. Subtraction
8. Conjecture is true
obstuse angle.
J
What is the Hinge Theorem?
• If two sides of one triangle are congruent
to another pair of sides in another
triangle, but the included angles are not
congruent, then the longer third side is
across the larger included angle.
• CONVERSE: The longer third side is across
the larger included angle if the included
angles of the triangles are not congruent
even though they have two sides with the
same length.
Example 1.
E
B
D
F
A
C
The measure of <A is less than the measure of <D, so EF is greater than BC.
Example 2.
J
G
K
H
I
The segment GI is greater than JL.
L
Example 3.
L
P
N
M
O
Q
All of the angles in the right triangles are congruent, but PQ is greater than LM.
Special Right Triangles
• 30-60-90: in a 30°-60°-90° triangle, the
length is the hypotenuse is 2 times the
length if the shorter leg, and the length
if the longest side is the length if the
shorter leg times √3.
• 45-45-90: in a 45°-45°-90° triangle, both
legs are congruent and the length of
the hypotenuse is the length if a leg
times √2.
Example 1 (45-45-90).
x
45°
The hypotenuse has to
be #√2.
So the measure is 6√2.
6
x = 6√2
Example 2 (45-45-90).
X
5 = x√2
5=x
√2
5√2 x
2
5
X = 5√2 ÷ 2
Example 3 (45-45-90).
45°
X = leg√2
X = 8√2
x
8
X = 8√2
Example 4 (30-60-90).
18 = 2x
9=x
60°
18
x
y
X = 9 and Y = 9√3
Y = x√3
Y = 9√3
30°
Example 5 (30-60-90).
12 = x√3
12/√3 = x
4√3 = x
60°
y
x
12
X = 4√3 and Y = 8√3
Y = 2x
Y = 2(4√3)
Y = 8√3
30°
Example 6 (30-60-90).
Y = 2x
Y = 2(8)
Y = 16
60°
y
8
8√3
30°
Y = 16