* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download G7-3 Measuring and Drawing Angles and Triangles
Technical drawing wikipedia , lookup
Multilateration wikipedia , lookup
Perspective (graphical) wikipedia , lookup
Trigonometric functions wikipedia , lookup
Euler angles wikipedia , lookup
Perceived visual angle wikipedia , lookup
Rational trigonometry wikipedia , lookup
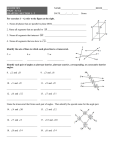
G7-3 Measuring and Drawing Angles and Triangles right angle 90° acute angles less than 90° obtuse angles more than 90° and less than 180° 1. Without using a protractor, identify each angle as acute or obtuse. a) b) c) d) 2. Practise choosing the correct scale to measure an angle. Step 1: Is the angle acute or obtuse? Circle your answer. Step 2: Circle the 2 numbers that the arm of the angle passes through. a) b) The angle is acute / obtuse. The angle measures The angle is acute / obtuse. °. The angle measures °. d) The angle is acute / obtuse. The angle measures COPYRIGHT © 2009 JUMP MATH: NOT TO BE COPIED c) 102 Step 3: Choose the correct angle measure. Example: if the angle is acute, the measure is less than 90°. The angle is acute / obtuse. °. The angle measures °. Geometry 7-3 3. Measure each angle. Hint: For parts d) and e), you will have to extend the arms. a) b) c) ° ° ° d) e) ° ° 4. In each polygon, circle angle XYZ . Then measure the angle. a) X b) Y Y X W Z Measure of XYZ : COPYRIGHT © 2009 JUMP MATH: NOT TO BE COPIED 5. ABC is 90°. ABD is 50°. U c) Z Z W V W Y Measure of XYZ : A V X Measure of XYZ : D Û B C a) What is the measure of DBC ? How do you know? b) Measure DBC with a protractor to check your answer in a). Geometry 7-3 103 G7-4 Perpendicular Lines Perpendicular lines meet at a right angle (90°). The ^ symbol means “is perpendicular to.” EG ^ ZF AB ^ ST S Z E B A G F T 1. Name the perpendicular lines. a) b) c) K d) S D A P B F B E D J C AB C E T ^ ^ A Q ^ ^ 2. Are the pairs of lines below perpendicular? Measure the angle where they meet to check. ) to show any perpendicular lines. Draw a square corner ( a) b) c) d) e) COPYRIGHT © 2009 JUMP MATH: NOT TO BE COPIED 3. Match the diagrams to the descriptions. A. B. A P B A C. P B A D. P B A B P point P on line segment AB lines that pass through point P on AB lines perpendicular to AB the line perpendicular to AB that passes through point P Geometry 7-4 105 ^ ^ ^ ^ G7-6 Parallel Lines Parallel lines never intersect, no matter how far they are extended in either direction. 1. Extend both lines. Use a ruler. Do the lines intersect or are they parallel? 2. Match the descriptions to the lines. A. The lines intersect. B. If the lines were extended far enough, they would intersect. C. The lines are parallel. 3. Give two examples of parallel lines in the world around you. We mark parallel lines using an equal number of arrow symbols (>, >>, and so on). The || symbol means “is parallel to.” B C Example: AB || CD. A D 4. Use arrow symbols to mark the sides or edges of these shapes that look like they are parallel. COPYRIGHT © 2009 JUMP MATH: NOT TO BE COPIED a) b) c) 5. State which lines are parallel. a) F b) A d) R E c) M X H B Y AB Geometry 7-6 || T U G S || L F G || 109 Determining If Two Lines Are Parallel If two lines are perpendicular to another line, then they are parallel. If two lines are parallel, any line perpendicular to one of the parallel lines will be perpendicular to the other. 6. Mark any parallel lines. State which lines are parallel. N U O a) b) B E c) A D M d) L R F K W X S V H V EF Y || B || J || K 7. Complete the statements. a) AB is parallel to C and || Q A B KL is perpendicular to CD, so KL is also perpendicular to b) AB || and QR ^ C . , so,QR ^ . 8. a) All the angles in a rectangle are right angles. R D L A B D C b) AD ^ AB and AD ^ , so AB || DC ^ AD and DC ^ , so AD || c) Explain how you know that these pairs of sides are parallel. COPYRIGHT © 2009 JUMP MATH: NOT TO BE COPIED Mark the right angles on this rectangle. 9. &LUFOHWKHÀDJVWKDWFRQWDLQSDUDOOHOOLQHVQRWFRXQWLQJWKHHGJHVRIWKHÀDJV 110 Geometry 7-6 G7-7 Angle Relationships shared arm a b a shared vertex straight angle A straight angle measures 180°. adjacent angles Adjacent angles a and b have a shared vertex and arm. b linear pair The sum of the angles in a linear pair is 180°. 1. Match the diagrams to the names. Hint: The angles in a linear pair are also adjacent angles. straight angle: A. a b adjacent angles: linear pair: B. C. b a a b 2. Calculate these angle sums. a) 10° + 25° = b) 30° + 40° = c) 12° + 28° = d) 20° + 30° + 40° = 3. 1 and 2 are a linear pair. Identify the three other linear pairs in the diagram. and and and 1 4 2 3 4. Determine the sum of the angles formed by two lines that intersect at a right angle. ∠1 + ∠2 = 90D + 90D = ∠3 + ∠4 = 90D + 90D = ° So, ∠1 + ∠2 + ∠3 + ∠4 °+ °= ° ° 1 2 3 4 5. Determine the sum of the angles formed by any two intersecting lines. So, ∠1 + ∠2 = ° and ∠3 + ∠4 = So, ∠1 + ∠2 + ∠3 + ∠4 = °. ° ° 6. Predict the sum of the four angles around any point P. 4 1 3 2 COPYRIGHT © 2009 JUMP MATH: NOT TO BE COPIED The sum of the angles in a linear pair is ° Calculate these angle sums to check your prediction. 95° 150° 30° 30° 150° 30° + 150° + 30° + 150° = 112 85° 85° 95° 95° + 85° + 95° + 85° = Geometry 7-7 ∠XZY ∠XZY = ∠A + ∠B + ∠C = 180 ∠$ ∠$ = 180 − (80 + 30 ) ∠) ∠$ = 180 − ∠$ =