Download Physics 11 Fall 2012 Practice Problems 7 - Solutions

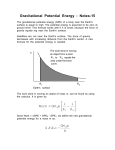
Physics 11 Fall 2012
Practice Problems 7 - Solutions
1. Why is the gravitational potential energy of two masses negative? Note that saying
“because that’s what the equation gives” is not an explanation!
————————————————————————————————————
Solution
The gravitational potential energy represents the energy of the system, which you can
think of as the amount of work that it took to put the system together. Because the
masses attract each other gravitationally, then they naturally fall together. This means
that the work was done for us, and so the system has negative energy. This is also the
amount of energy that we’d need to add to the system to break it apart. Since we’d
need to do work on the system to break it apart (ending up with zero total energy), we
had to start with a negative energy. The same thing occurs with oppositely-charged
particles like protons and electrons, which also have negative electrostatic potential
energy.
1
2. One of the greatest discoveries in astronomy in the past decade is the detection of
planets outside the solar system. Since 1996, more than 100 planets have been detected
orbiting stars other than the Sun. While the planets themselves cannot be seen directly,
telescopes can detect the small periodic motion of the star as the star and planet orbit
around their common center of mass. (This is measured using the Doppler effect.)
Both the period of this motion and the variation in speed of the star over the course
of time can be determined observationally. The mass of the star is found from its
observed luminance and from the theory of stellar structure. Iota Draconis is the
eighth brightest star in the constellation Draco. Observations show that a planet, with
an orbital period 1.50 y, is orbiting this star. The mass of Iota Draconis is 1.05MSun .
(a) Estimate the size (in AU) of the semimajor axis of this planet’s orbit.
(b) The radial speed of the star is observed to vary by 592 m/s. Use conservation of
momentum to find the mass of the planet. Assume the orbit is circular, we are
observing the orbit edge-on, and no other planets orbit Iota Draconis. Express
the mass as a multiple of the mass of Jupiter.
————————————————————————————————————
Solution
(a) We can determine the semimajor axis using Kepler’s law, which says that T 2 =
4π 2 3
a , where T is the period (in years), M is the mass of the star, and a is the
GM
size of the semimajor axis (in AU). So, solving for a gives
a3 =
GM T 2
.
4π 2
Now, we can write M = 1.05MSun , and T = 1.5TEarth , so a3 = 1.05(1.5)2 C =
T2
= 1 is just the orbital period of the Earth, one year!
1.05(1.5)2 , since a3 = GM
4π 2
So, we just find a = (1.05(1.52 ))1/3 = 1.33 AU.
(b) The star and it’s planet are orbiting about their common center of mass. We can
treat this like an elastic collision problem in which the momentum is conserved.
In this case the momentum of each body is equal mv = M V , where m is the mass
of the planet with velocity v, and M is the mass of the star with velocity V . If
the velocity is found to change by a certain amount in the elastic collision, then
the velocity of the star is half that change by conservation of momentum (it starts
off heading one way, then it heads the other after the collision). Solving for the
mass of the planet is m = Vv M . The velocity of the planet is just v = 2πa/T , so
VT
M.
2πa
Now, plugging in the different values, and recalling that the mass of Jupiter is
mJ = 1.90 × 1027 kg, gives
m=
m=
1
592(1.50
2
× 365 × 24 × 3600)
(1.05 × 2 × 1030 ) = 2.33 × 1028 kg = 12.5mJ .
2π(1.33 × 1.5 × 1011 )
2
3. Some people think that the shuttle astronauts are “weightless” because they are “beyond the pull of Earth’s gravity.” In fact, this is completely untrue.
(a) What is the magnitude of the gravitational field in the vicinity of a shuttle orbit?
A shuttle orbit is about 400 km above the ground.
(b) Given the answer in Part (a), explain why shuttle astronauts suffer from adverse biological effects such as muscle atrophy even though the are not actually
“weightless.”
————————————————————————————————————
Solution
(a) The shuttle orbits at a distance of r = RE + h from the center of the Earth, where
RE is the radius of the Earth, and h is the height above the surface. If the height
is h = 400 km, then r = 6400 + 400 = 6800 km, or 6.8 × 106 meters. At this
point, the gravitational field has a magnitude
g=
6.67 × 10−11 × 5.98 × 1024
GME
=
= 8.6 m/s2 ,
r2
(6.8 × 106 )2
which is still almost 90% of the acceleration at the surface of the Earth.
(b) Remember that the weight that we feel is due to the normal force. The astronauts
in orbit are in constant free-fall, and don’t feel their weight. So, without the
compensating normal force to fight against the muscles begin to weaken, not
needing to do as much anymore.
3
4. Calculate the mass of Earth from the period of the moon, T = 27.3 d; its mean orbital
radius rm = 3.84 × 108 m; and the known value of G.
————————————————————————————————————
Solution
Earth
, where
The moon is held to the Earth by the gravitational force, FG = G mmoonrM
2
r is the orbital radius. Now, because the orbit is (pretty much) circular, then the net
v2
. But, for an object moving
force on the moon is the centripetal force, Fcent = mmoon
r
in a circle, then v = 2πr/T , and so
Fcent
mmoon
=
r
2πr
T2
2
=
4π 2
mmoon r.
T2
Because the orbit is stable this force is equal to the gravitational force. Setting the
two forces equal gives
mmoon MEarth
4π 2
mmoon r = G
.
2
T
r2
Solving for the mass of the Earth gives
MEarth =
4π 2 3
r .
T 2G
The period is T = 27.3 × 3600 × 24 = 2.36 × 106 seconds, and so
MEarth =
4π 2 3
4π 2
r
=
(3.84 × 108 )3 = 6 × 1024 kg.
T 2G
(2.36 × 106 )2 (6.672 × 10−11 )
4
5. The Principle of Equivalence states that the free-fall acceleration of any object in a
gravitational field is independent of the mass of the object. This can be deduced
from the law of universal gravitation, but how well does it hold up experimentally?
The Roll-Krotkov-Dicke experiment performed in the 1960s indicates that the free-fall
acceleration is independent of mass to at least 1 part in 1012 . Suppose two objects are
simultaneously released from rest in a uniform gravitational field. Also, suppose one of
the object falls with a constant acceleration of exactly 9.81 m/s2 , while the other falls
with a constant acceleration that is greater than 9.81 m/s2 by one part in 1012 . How
far will the first object have fallen when the second object has fallen 1.00 mm farther
than the first object has? Note that this estimate provides only an upper bound on
the difference in the accelerations; most physicists believe that there is no difference in
the accelerations.
————————————————————————————————————
Solution
The first object has an acceleration g = 9.81 m/s2 , while the other has a different
acceleration, g + ∆g = 9.81 (1 + 10−12 ) m/s2 , where ∆g = 9.81 × 10−12 m/s2 . Now,
if released from rest, the first object will fall a distance d1 = 21 gt2 , while the second
object will have fallen a distance d2 = 12 (g + ∆g)t2 = 21 gt2 + 21 ∆gt2 . Now, the difference
in distance that the two objects will have fallen is ∆d = d2 − d1 = 21 ∆gt2 .
p
Now, solving d1 = 21 gt2 for the time of fall gives t = 2d1 /g. Plugging this in for ∆d
gives
1
2d1
∆g
∆d = ∆g
=
d1 .
2
g
g
Now, solving for the distance, recalling that ∆g = 10−12 g, we find
d1 =
g
∆d = 1012 ∆d.
∆g
So, if the first object has traveled an extra distance ∆d = 10−3 m, then the distance
that it’s fallen will have been
d1 = 1012 ∆d = 1012 × 10−3 = 109 m.
So, the two objects will have to fall a distance of a billion meters to get out of step by
1 millimeter!
5
6. (a) If we take the potential energy of a 100 kg object and Earth to be zero when the
two are separated by an infinite distance, what is the potential energy when the
object is at the surface of Earth?
(b) Find the potential energy of the same object at a height above Earth’s surface
equal to Earth’s radius.
(c) Find the escape speed for a body projected from this height.
————————————————————————————————————
Solution
(a) The gravitational potential energy of two objects of masses m and M , separated
by a distance r is
mM
,
P Egrav = −G
r
which sets the potential energy to zero when the objects are infinitely far apart
(r → ∞). So, if the object is on the surface of the Earth, then r = RE , and
M = ME , and
mME
P Eg = −G
.
RE
Now, we can rewrite this recalling that for Earth, g =
P Eg = −G
GME
2 .
RE
Thus,
mME
GME
= −m 2 RE = −mgRE .
RE
RE
Now, if the radius of the Earth is 6400 km, or 6.4 × 106 meters, then
P Eg = −mgRE = −(100)(9.8)(6.4 × 106 ) = −6.3 × 109 J.
(b) The potential energy at a distance of r = RE + RE = 2RE will just be
P Eg = −G
mME
1
= − mgRE = −3.15 × 109 J.
2RE
2
(c) To determine the escape velocity from this distance we just recall the usual method
setting KE + P E = 0, so 21 mv 2 = 12 mgRE , giving
vesc =
p
p
gRE = (9.8)(6.4 × 103 ) = 8 km/s,
which is smaller than the escape velocity from the surface of the earth (vesc ≈ 11
km/s), as we should expect.
6
7. A point particle of mass m is on the x axis at x = L and an identical point particle is
on the y axis at y = L.
(a) What is the direction of the gravitational field at the origin?
(b) What is the magnitude of this field?
————————————————————————————————————
Solution
(a) The mass m at x = L creates a gravitational field ~gx = Gm
î at the origin, while
L2
Gm
the mass at y = L creates a field ~gy = L2 ĵ at the origin. The net gravitational
field at the origin is just the sum of the two fields, ~g = ~gx + ~gy , or
m
~g = G 2 î + ĵ .
L
√
√
p
(b) The magnitude of the field is g = |~g | = gx2 + gy2 = G Lm2 12 + 12 = 2Gm
.
L2
7
8. A straight, smooth tunnel is dug through a uniform spherical planet of mass density
ρ0 . The tunnel passes though the center of the planet and is perpendicular to the
planet’s axis of rotation, which is fixed in space. The planet rotates with a constant
angular speed ω, so objects in the tunnel have no apparent weight. Find the required
angular speed of the planet ω.
————————————————————————————————————
Solution
, where M is the planetary
The object falls due to the gravitational force, FG = G mM
r2
mass beneath the object (recall that only the mass between an object and the center of
the planet makes any difference, gravitationally). Let’s figure out how much mass this
is.
Because the density is constant, then the total mass inside a radius r is Min = ρ0 Vin =
r3 . So, the net gravitational force on the object is
ρ0 4π
3
FG = G
4πGmρ0
mMin
=
r.
2
r
3
2
At some radius, the gravitational force is balanced by the centripetal force, Fcent = mvr ,
causing it to seem to be weightless. Since v = rω, we can write Fcent = mrω 2 . Setting
the two forces equal gives
4πGmρ0
r = mrω 2 .
3
Notice that the mass and radius of the object cancels out. Solving for the angular
speed gives
r
4πGρ0
ω=
.
3
8
9. Black holes are objects whose gravitational field is so strong that not even light can
escape. One way of thinking about this is to consider a spherical object whose density
is so large that the escape speed at its surface is greater than the speed of light, c. If a
star’s radius is smaller than a value called the Schwarzschild radius RS , then the star
will be a black hole, that is, light originating from its surface cannot escape.
(a) For a nonrotating black hole, the Schwarzschild radius depends only upon the mass
of the black hole. Show that it is related to that mass M by RS = (2GM ) /c2 .
(b) Calculate the value of the Schwarzschild radius for a black hole whose mass is ten
solar masses.
————————————————————————————————————
Solution
(a) The escape velocity of a spherical mass M with radius R is given by
r
2GM
.
vesc =
r
If we want light to be unable to escape from the surface, then the escape velocity
has to be greater than, or equal to, the speed of light. Thus, setting the escape
velocity vesc = c and solving for the radius gives
RS =
2GM
.
c2
(b) The mass of the sun, Msun = 2 × 1030 kg. So, we can determine the Schwarzschild
radius for this black hole,
RS =
2GM
2 × 6.67 × 10−11 × 10 × 2 × 1030
=
= 29.6 km.
c2
(3 × 108 )2
So, the mass of ten suns is squashed into a ball about the size of a large city.
9
10. It is believed that there is a “supermassive” black hole at the center of our galaxy.
One datum that leads to this conclusion is the important recent observation of stellar
motion in the vicinity of the galactic center. If one such star moves in an elliptical orbit
with a period of 15.2 years and has semimajor axis of 5.5 light days (the distance light
travels in 5.5 days), what is the mass around which the star moves in its Keplerian
orbit?
————————————————————————————————————
Solution
Kepler’s law says that the square of the period, T , of an orbit is proportional to the
cube of it’s semimajor axis, a, so
T2 =
4π 2 3
a.
GM
So, all we need to do is to solve for the mass,
M=
4π 2 3
a.
GT 2
Now, we can just plug in numbers. One year has about π × 107 seconds, while one
day has 3600 × 24 = 86400 seconds. So, one light day is 3 × 108 × 86400 = 2.6 × 1013
meters. So,
4π 2
4π 2 3
13 3
a
=
5.5
×
2.6
×
10
M=
= 7.5 × 1036 kg.
2
−11
7
2
GT
6.7 × 10 (15.2 × π × 10 )
Our sun has a mass of about 2 × 1030 kg, and so this star has a mass of nearly four
million suns! This is clearly a black hole.
10